Attention is a smoothed cubic spline

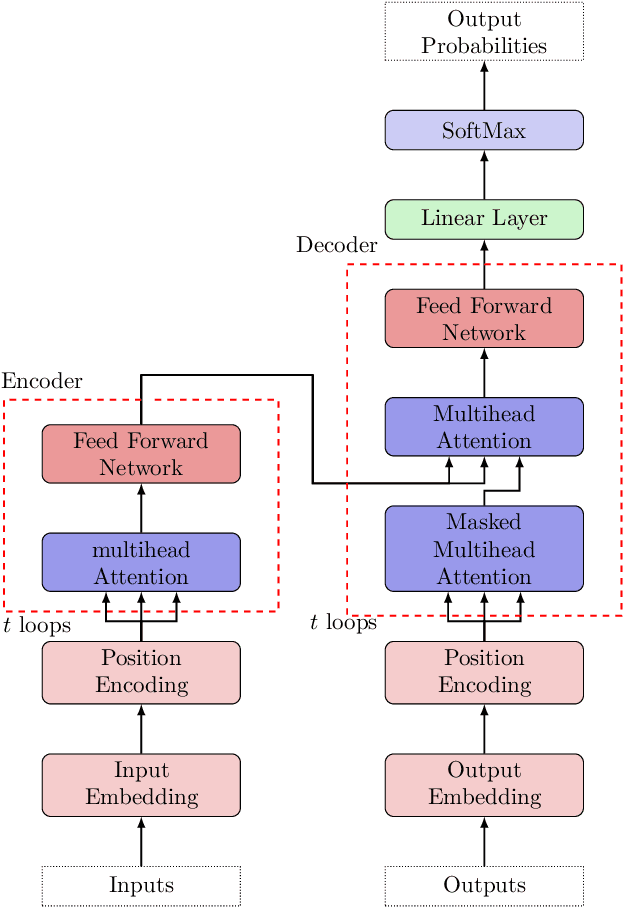
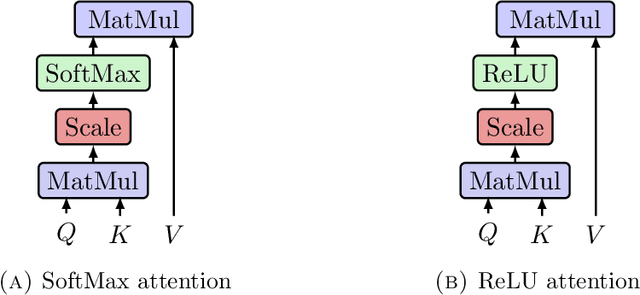
We highlight a perhaps important but hitherto unobserved insight: The attention module in a transformer is a smoothed cubic spline. Viewed in this manner, this mysterious but critical component of a transformer becomes a natural development of an old notion deeply entrenched in classical approximation theory. More precisely, we show that with ReLU-activation, attention, masked attention, encoder-decoder attention are all cubic splines. As every component in a transformer is constructed out of compositions of various attention modules (= cubic splines) and feed forward neural networks (= linear splines), all its components -- encoder, decoder, and encoder-decoder blocks; multilayered encoders and decoders; the transformer itself -- are cubic or higher-order splines. If we assume the Pierce-Birkhoff conjecture, then the converse also holds, i.e., every spline is a ReLU-activated encoder. Since a spline is generally just $C^2$, one way to obtain a smoothed $C^\infty$-version is by replacing ReLU with a smooth activation; and if this activation is chosen to be SoftMax, we recover the original transformer as proposed by Vaswani et al. This insight sheds light on the nature of the transformer by casting it entirely in terms of splines, one of the best known and thoroughly understood objects in applied mathematics.

On the Utility Recovery Incapability of Neural Net-based Differential Private Tabular Training Data Synthesizer under Privacy Deregulation

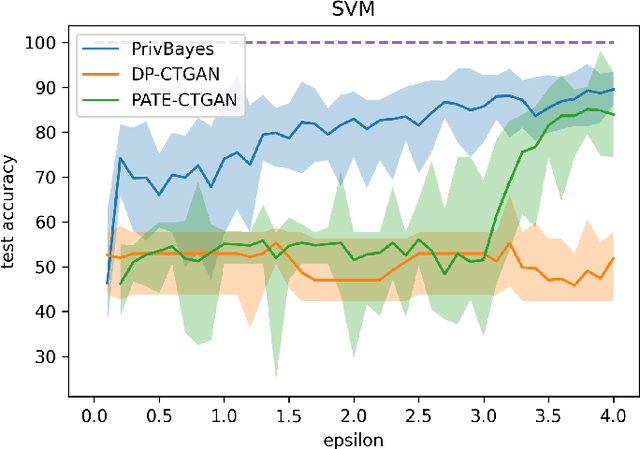
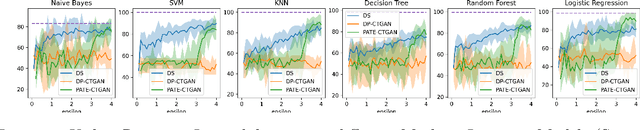
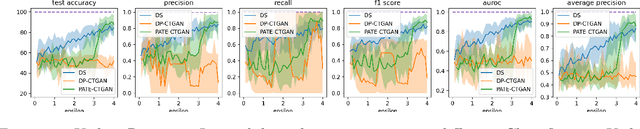
Devising procedures for auditing generative model privacy-utility tradeoff is an important yet unresolved problem in practice. Existing works concentrates on investigating the privacy constraint side effect in terms of utility degradation of the train on synthetic, test on real paradigm of synthetic data training. We push such understanding on privacy-utility tradeoff to next level by observing the privacy deregulation side effect on synthetic training data utility. Surprisingly, we discover the Utility Recovery Incapability of DP-CTGAN and PATE-CTGAN under privacy deregulation, raising concerns on their practical applications. The main message is Privacy Deregulation does NOT always imply Utility Recovery.

LU decomposition and Toeplitz decomposition of a neural network

It is well-known that any matrix $A$ has an LU decomposition. Less well-known is the fact that it has a 'Toeplitz decomposition' $A = T_1 T_2 \cdots T_r$ where $T_i$'s are Toeplitz matrices. We will prove that any continuous function $f : \mathbb{R}^n \to \mathbb{R}^m$ has an approximation to arbitrary accuracy by a neural network that takes the form $L_1 \sigma_1 U_1 \sigma_2 L_2 \sigma_3 U_2 \cdots L_r \sigma_{2r-1} U_r$, i.e., where the weight matrices alternate between lower and upper triangular matrices, $\sigma_i(x) := \sigma(x - b_i)$ for some bias vector $b_i$, and the activation $\sigma$ may be chosen to be essentially any uniformly continuous nonpolynomial function. The same result also holds with Toeplitz matrices, i.e., $f \approx T_1 \sigma_1 T_2 \sigma_2 \cdots \sigma_{r-1} T_r$ to arbitrary accuracy, and likewise for Hankel matrices. A consequence of our Toeplitz result is a fixed-width universal approximation theorem for convolutional neural networks, which so far have only arbitrary width versions. Since our results apply in particular to the case when $f$ is a general neural network, we may regard them as LU and Toeplitz decompositions of a neural network. The practical implication of our results is that one may vastly reduce the number of weight parameters in a neural network without sacrificing its power of universal approximation. We will present several experiments on real data sets to show that imposing such structures on the weight matrices sharply reduces the number of training parameters with almost no noticeable effect on test accuracy.

Regularizing Deep Neural Networks with Stochastic Estimators of Hessian Trace

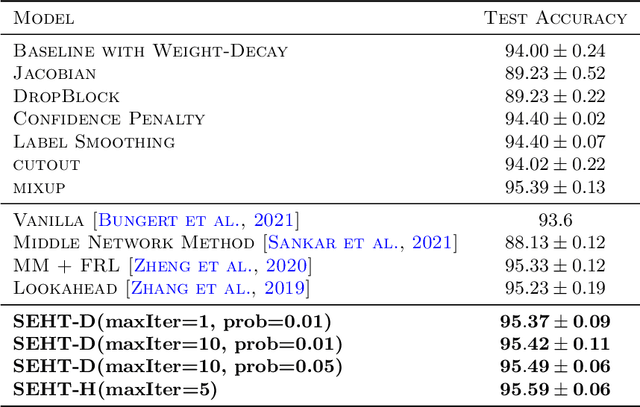
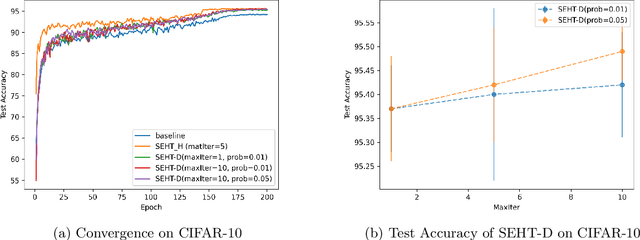
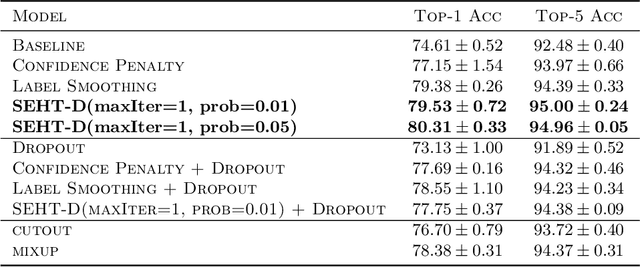
In this paper we develop a novel regularization method for deep neural networks by penalizing the trace of Hessian. This regularizer is motivated by a recent guarantee bound of the generalization error. Hutchinson method is a classical unbiased estimator for the trace of a matrix, but it is very time-consuming on deep learning models. Hence a dropout scheme is proposed to efficiently implements the Hutchinson method. Then we discuss a connection to linear stability of a nonlinear dynamical system and flat/sharp minima. Experiments demonstrate that our method outperforms existing regularizers and data augmentation methods, such as Jacobian, confidence penalty, and label smoothing, cutout and mixup.

GraphPrompt: Biomedical Entity Normalization Using Graph-based Prompt Templates

Biomedical entity normalization unifies the language across biomedical experiments and studies, and further enables us to obtain a holistic view of life sciences. Current approaches mainly study the normalization of more standardized entities such as diseases and drugs, while disregarding the more ambiguous but crucial entities such as pathways, functions and cell types, hindering their real-world applications. To achieve biomedical entity normalization on these under-explored entities, we first introduce an expert-curated dataset OBO-syn encompassing 70 different types of entities and 2 million curated entity-synonym pairs. To utilize the unique graph structure in this dataset, we propose GraphPrompt, a prompt-based learning approach that creates prompt templates according to the graphs. GraphPrompt obtained 41.0% and 29.9% improvement on zero-shot and few-shot settings respectively, indicating the effectiveness of these graph-based prompt templates. We envision that our method GraphPrompt and OBO-syn dataset can be broadly applied to graph-based NLP tasks, and serve as the basis for analyzing diverse and accumulating biomedical data.