Regularizing Deep Neural Networks with Stochastic Estimators of Hessian Trace
Paper and Code
Aug 11, 2022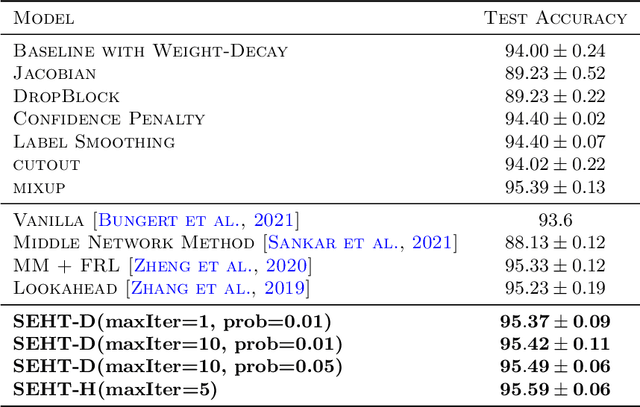
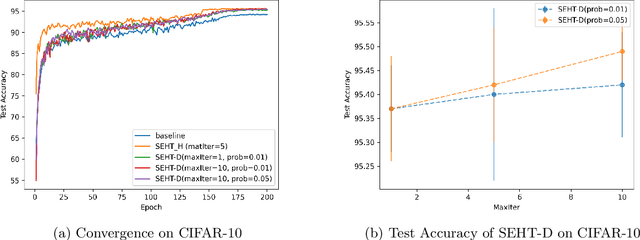
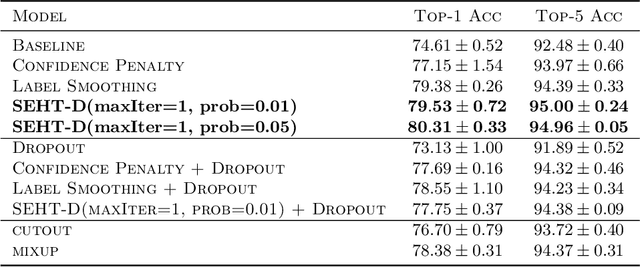

In this paper we develop a novel regularization method for deep neural networks by penalizing the trace of Hessian. This regularizer is motivated by a recent guarantee bound of the generalization error. Hutchinson method is a classical unbiased estimator for the trace of a matrix, but it is very time-consuming on deep learning models. Hence a dropout scheme is proposed to efficiently implements the Hutchinson method. Then we discuss a connection to linear stability of a nonlinear dynamical system and flat/sharp minima. Experiments demonstrate that our method outperforms existing regularizers and data augmentation methods, such as Jacobian, confidence penalty, and label smoothing, cutout and mixup.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge