Universal Segmentation of 33 Anatomies

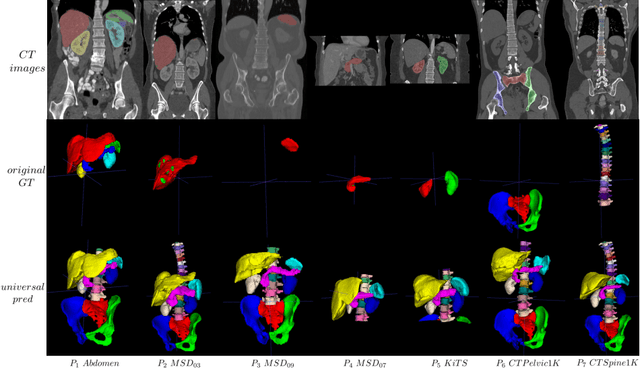
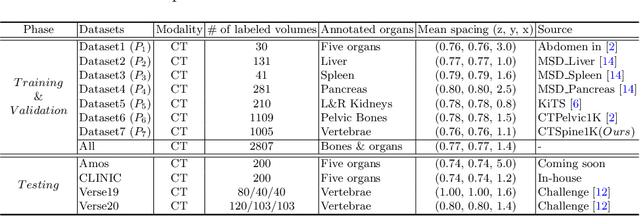
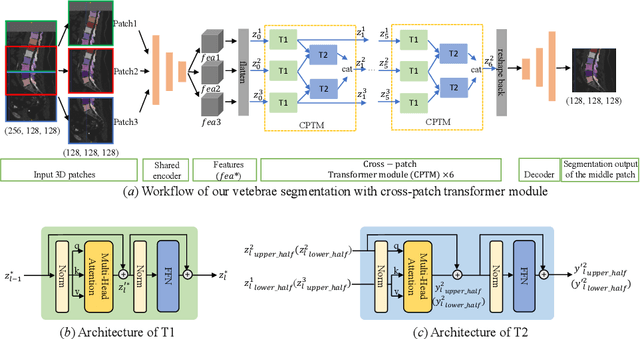
In the paper, we present an approach for learning a single model that universally segments 33 anatomical structures, including vertebrae, pelvic bones, and abdominal organs. Our model building has to address the following challenges. Firstly, while it is ideal to learn such a model from a large-scale, fully-annotated dataset, it is practically hard to curate such a dataset. Thus, we resort to learn from a union of multiple datasets, with each dataset containing the images that are partially labeled. Secondly, along the line of partial labelling, we contribute an open-source, large-scale vertebra segmentation dataset for the benefit of spine analysis community, CTSpine1K, boasting over 1,000 3D volumes and over 11K annotated vertebrae. Thirdly, in a 3D medical image segmentation task, due to the limitation of GPU memory, we always train a model using cropped patches as inputs instead a whole 3D volume, which limits the amount of contextual information to be learned. To this, we propose a cross-patch transformer module to fuse more information in adjacent patches, which enlarges the aggregated receptive field for improved segmentation performance. This is especially important for segmenting, say, the elongated spine. Based on 7 partially labeled datasets that collectively contain about 2,800 3D volumes, we successfully learn such a universal model. Finally, we evaluate the universal model on multiple open-source datasets, proving that our model has a good generalization performance and can potentially serve as a solid foundation for downstream tasks.

CTSpine1K: A Large-Scale Dataset for Spinal Vertebrae Segmentation in Computed Tomography

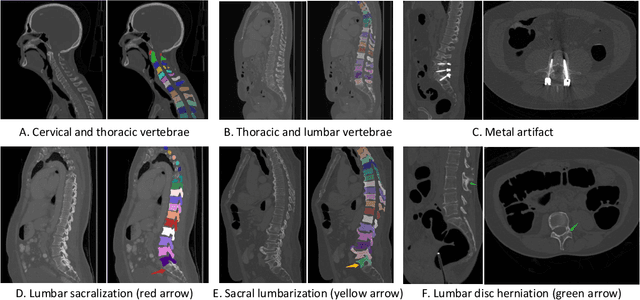
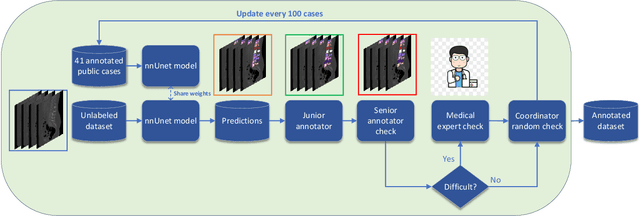
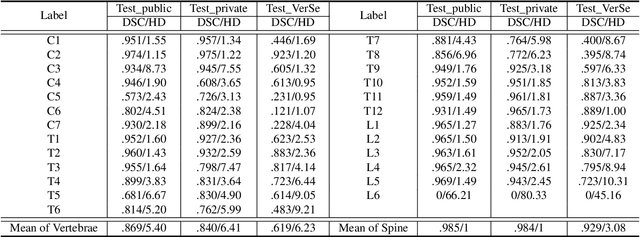
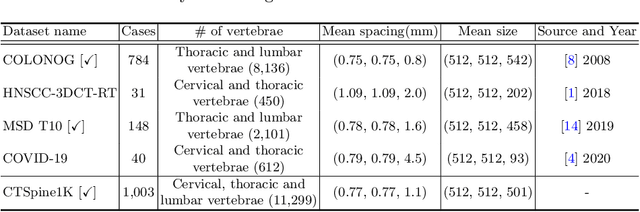
Spine-related diseases have high morbidity and cause a huge burden of social cost. Spine imaging is an essential tool for noninvasively visualizing and assessing spinal pathology. Segmenting vertebrae in computed tomography (CT) images is the basis of quantitative medical image analysis for clinical diagnosis and surgery planning of spine diseases. Current publicly available annotated datasets on spinal vertebrae are small in size. Due to the lack of a large-scale annotated spine image dataset, the mainstream deep learning-based segmentation methods, which are data-driven, are heavily restricted. In this paper, we introduce a large-scale spine CT dataset, called CTSpine1K, curated from multiple sources for vertebra segmentation, which contains 1,005 CT volumes with over 11,100 labeled vertebrae belonging to different spinal conditions. Based on this dataset, we conduct several spinal vertebrae segmentation experiments to set the first benchmark. We believe that this large-scale dataset will facilitate further research in many spine-related image analysis tasks, including but not limited to vertebrae segmentation, labeling, 3D spine reconstruction from biplanar radiographs, image super-resolution, and enhancement.

Dual affine moment invariants

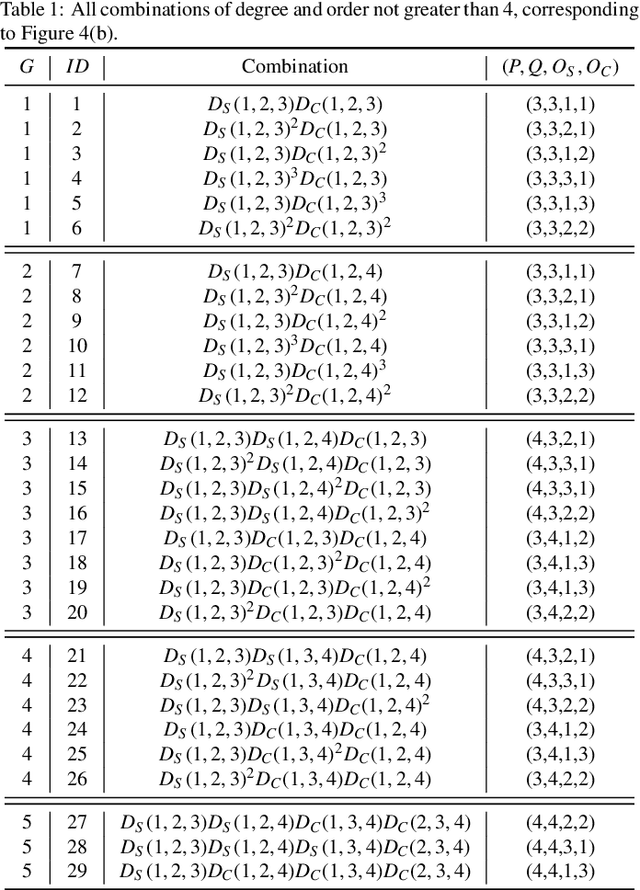
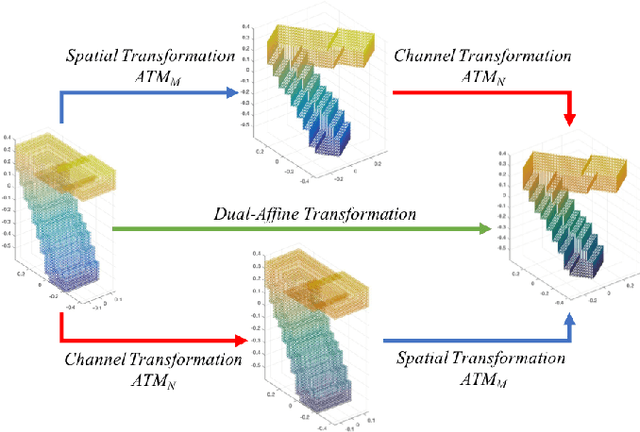
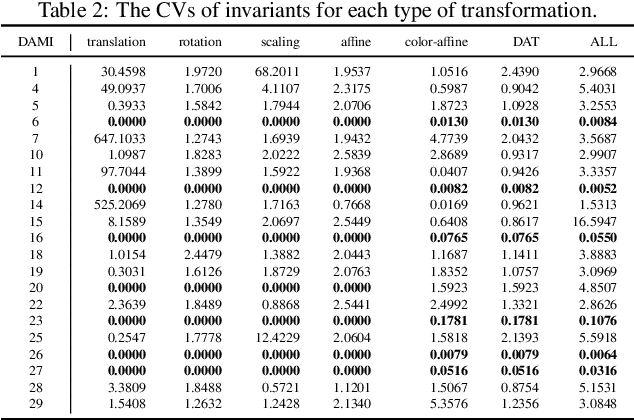
Affine transformation is one of the most common transformations in nature, which is an important issue in the field of computer vision and shape analysis. And affine transformations often occur in both shape and color space simultaneously, which can be termed as Dual-Affine Transformation (DAT). In general, we should derive invariants of different data formats separately, such as 2D color images, 3D color objects, or even higher-dimensional data. To the best of our knowledge, there is no general framework to derive invariants for all of these data formats. In this paper, we propose a general framework to derive moment invariants under DAT for objects in M-dimensional space with N channels, which can be called dual-affine moment invariants (DAMI). Following this framework, we present the generating formula of DAMI under DAT for 3D color objects. Then, we instantiated a complete set of DAMI for 3D color objects with orders and degrees no greater than 4. Finally, we analyze the characteristic of these DAMI and conduct classification experiments to evaluate the stability and discriminability of them. The results prove that DAMI is robust for DAT. Our derivation framework can be applied to data in any dimension with any number of channels.

Differential and integral invariants under Mobius transformation

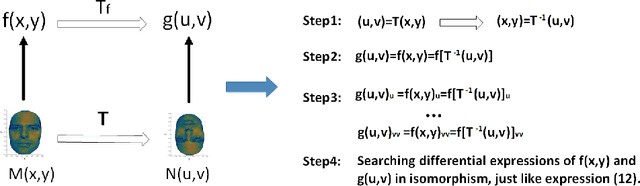
One of the most challenging problems in the domain of 2-D image or 3-D shape is to handle the non-rigid deformation. From the perspective of transformation groups, the conformal transformation is a key part of the diffeomorphism. According to the Liouville Theorem, an important part of the conformal transformation is the Mobius transformation, so we focus on Mobius transformation and propose two differential expressions that are invariable under 2-D and 3-D Mobius transformation respectively. Next, we analyze the absoluteness and relativity of invariance on them and their components. After that, we propose integral invariants under Mobius transformation based on the two differential expressions. Finally, we propose a conjecture about the structure of differential invariants under conformal transformation according to our observation on the composition of the above two differential invariants.

Fast and Efficient Calculations of Structural Invariants of Chirality

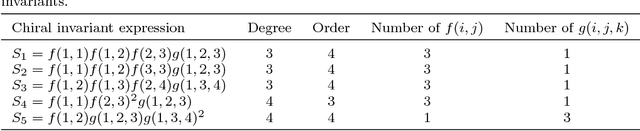
Chirality plays an important role in physics, chemistry, biology, and other fields. It describes an essential symmetry in structure. However, chirality invariants are usually complicated in expression or difficult to evaluate. In this paper, we present five general three-dimensional chirality invariants based on the generating functions. And the five chiral invariants have four characteristics:(1) They play an important role in the detection of symmetry, especially in the treatment of 'false zero' problem. (2) Three of the five chiral invariants decode an universal chirality index. (3) Three of them are proposed for the first time. (4) The five chiral invariants have low order no bigger than 4, brief expression, low time complexity O(n) and can act as descriptors of three-dimensional objects in shape analysis. The five chiral invariants give a geometric view to study the chiral invariants. And the experiments show that the five chirality invariants are effective and efficient, they can be used as a tool for symmetry detection or features in shape analysis.

Naturally Combined Shape-Color Moment Invariants under Affine Transformations

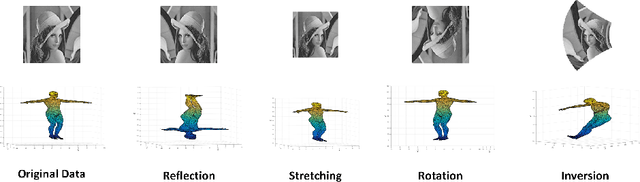
We proposed a kind of naturally combined shape-color affine moment invariants (SCAMI), which consider both shape and color affine transformations simultaneously in one single system. In the real scene, color and shape deformations always exist in images simultaneously. Simple shape invariants or color invariants can not be qualified for this situation. The conventional method is just to make a simple linear combination of the two factors. Meanwhile, the manual selection of weights is a complex issue. Our construction method is based on the multiple integration framework. The integral kernel is assigned as the continued product of the shape and color invariant cores. It is the first time to directly derive an invariant to dual affine transformations of shape and color. The manual selection of weights is no longer necessary, and both the shape and color transformations are extended to affine transformation group. With the various of invariant cores, a set of lower-order invariants are constructed and the completeness and independence are discussed detailedly. A set of SCAMIs, which called SCAMI24, are recommended, and the effectiveness and robustness have been evaluated on both synthetic and real datasets.

A Kind of Affine Weighted Moment Invariants

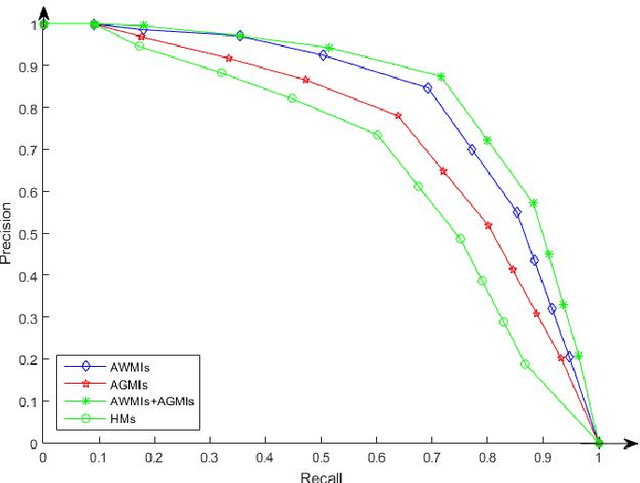
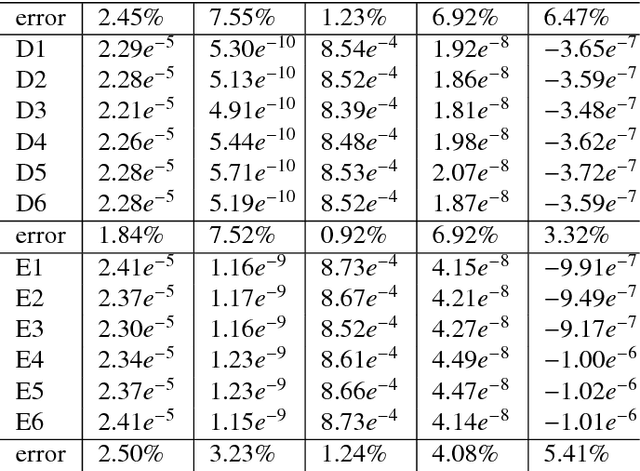
A new kind of geometric invariants is proposed in this paper, which is called affine weighted moment invariant (AWMI). By combination of local affine differential invariants and a framework of global integral, they can more effectively extract features of images and help to increase the number of low-order invariants and to decrease the calculating cost. The experimental results show that AWMIs have good stability and distinguishability and achieve better results in image retrieval than traditional moment invariants. An extension to 3D is straightforward.

Shape-Color Differential Moment Invariants under Affine Transformations

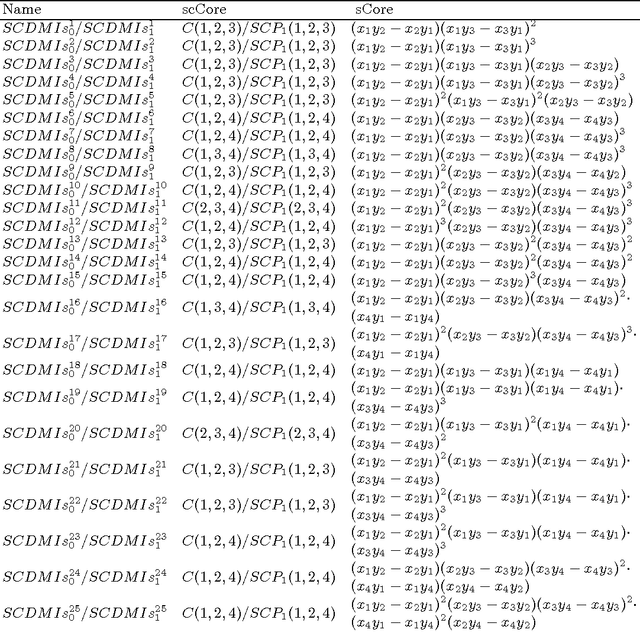
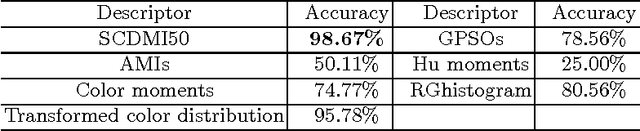
We propose the general construction formula of shape-color primitives by using partial differentials of each color channel in this paper. By using all kinds of shape-color primitives, shape-color differential moment invariants can be constructed very easily, which are invariant to the shape affine and color affine transforms. 50 instances of SCDMIs are obtained finally. In experiments, several commonly used color descriptors and SCDMIs are used in image classification and retrieval of color images, respectively. By comparing the experimental results, we find that SCDMIs get better results.

Affine-Gradient Based Local Binary Pattern Descriptor for Texture Classiffication

We present a novel Affine-Gradient based Local Binary Pattern (AGLBP) descriptor for texture classification. It is very hard to describe complicated texture using single type information, such as Local Binary Pattern (LBP), which just utilizes the sign information of the difference between the pixel and its local neighbors. Our descriptor has three characteristics: 1) In order to make full use of the information contained in the texture, the Affine-Gradient, which is different from Euclidean-Gradient and invariant to affine transformation is incorporated into AGLBP. 2) An improved method is proposed for rotation invariance, which depends on the reference direction calculating respect to local neighbors. 3) Feature selection method, considering both the statistical frequency and the intraclass variance of the training dataset, is also applied to reduce the dimensionality of descriptors. Experiments on three standard texture datasets, Outex12, Outex10 and KTH-TIPS2, are conducted to evaluate the performance of AGLBP. The results show that our proposed descriptor gets better performance comparing to some state-of-the-art rotation texture descriptors in texture classification.