Achieving Rotation Invariance in Convolution Operations: Shifting from Data-Driven to Mechanism-Assured

Achieving rotation invariance in deep neural networks without relying on data has always been a hot research topic. Intrinsic rotation invariance can enhance the model's feature representation capability, enabling better performance in tasks such as multi-orientation object recognition and detection. Based on various types of non-learnable operators, including gradient, sort, local binary pattern, maximum, etc., this paper designs a set of new convolution operations that are natually invariant to arbitrary rotations. Unlike most previous studies, these rotation-invariant convolutions (RIConvs) have the same number of learnable parameters and a similar computational process as conventional convolution operations, allowing them to be interchangeable. Using the MNIST-Rot dataset, we first verify the invariance of these RIConvs under various rotation angles and compare their performance with previous rotation-invariant convolutional neural networks (RI-CNNs). Two types of RIConvs based on gradient operators achieve state-of-the-art results. Subsequently, we combine RIConvs with different types and depths of classic CNN backbones. Using the OuTex_00012, MTARSI, and NWPU-RESISC-45 datasets, we test their performance on texture recognition, aircraft type recognition, and remote sensing image classification tasks. The results show that RIConvs significantly improve the accuracy of these CNN backbones, especially when the training data is limited. Furthermore, we find that even with data augmentation, RIConvs can further enhance model performance.

Sorted Convolutional Network for Achieving Continuous Rotational Invariance

The topic of achieving rotational invariance in convolutional neural networks (CNNs) has gained considerable attention recently, as this invariance is crucial for many computer vision tasks such as image classification and matching. In this letter, we propose a Sorting Convolution (SC) inspired by some hand-crafted features of texture images, which achieves continuous rotational invariance without requiring additional learnable parameters or data augmentation. Further, SC can directly replace the conventional convolution operations in a classic CNN model to achieve its rotational invariance. Based on MNIST-rot dataset, we first analyze the impact of convolutional kernel sizes, different sampling and sorting strategies on SC's rotational invariance, and compare our method with previous rotation-invariant CNN models. Then, we combine SC with VGG, ResNet and DenseNet, and conduct classification experiments on popular texture and remote sensing image datasets. Our results demonstrate that SC achieves the best performance in the aforementioned tasks.

Image Moment Invariants to Rotational Motion Blur

Rotational motion blur caused by the circular motion of the camera or/and object is common in life. Identifying objects from images affected by rotational motion blur is challenging because this image degradation severely impacts image quality. Therefore, it is meaningful to develop image invariant features under rotational motion blur and then use them in practical tasks, such as object classification and template matching. This paper proposes a novel method to generate image moment invariants under general rotational motion blur and provides some instances. Further, we achieve their invariance to similarity transform. To the best of our knowledge, this is the first time that moment invariants for rotational motion blur have been proposed in the literature. We conduct extensive experiments on various image datasets disturbed by similarity transform and rotational motion blur to test these invariants' numerical stability and robustness to image noise. We also demonstrate their performance in image classification and handwritten digit recognition. Current state-of-the-art blur moment invariants and deep neural networks are chosen for comparison. Our results show that the moment invariants proposed in this paper significantly outperform other features in various tasks.

RIC-CNN: Rotation-Invariant Coordinate Convolutional Neural Network

In recent years, convolutional neural network has shown good performance in many image processing and computer vision tasks. However, a standard CNN model is not invariant to image rotations. In fact, even slight rotation of an input image will seriously degrade its performance. This shortcoming precludes the use of CNN in some practical scenarios. Thus, in this paper, we focus on designing convolutional layer with good rotation invariance. Specifically, based on a simple rotation-invariant coordinate system, we propose a new convolutional operation, called Rotation-Invariant Coordinate Convolution (RIC-C). Without additional trainable parameters and data augmentation, RIC-C is naturally invariant to arbitrary rotations around the input center. Furthermore, we find the connection between RIC-C and deformable convolution, and propose a simple but efficient approach to implement RIC-C using Pytorch. By replacing all standard convolutional layers in a CNN with the corresponding RIC-C, a RIC-CNN can be derived. Using MNIST dataset, we first evaluate the rotation invariance of RIC-CNN and compare its performance with most of existing rotation-invariant CNN models. It can be observed that RIC-CNN achieves the state-of-the-art classification on the rotated test dataset of MNIST. Then, we deploy RIC-C to VGG, ResNet and DenseNet, and conduct the classification experiments on two real image datasets. Also, a shallow CNN and the corresponding RIC-CNN are trained to extract image patch descriptors, and we compare their performance in patch verification. These experimental results again show that RIC-C can be easily used as drop in replacement for standard convolutions, and greatly enhances the rotation invariance of CNN models designed for different applications.

Gaussian-Hermite Moment Invariants of General Vector Functions to Rotation-Affine Transform

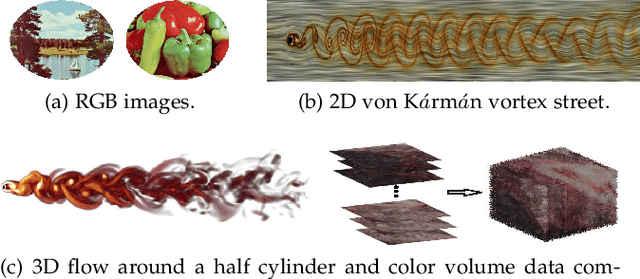
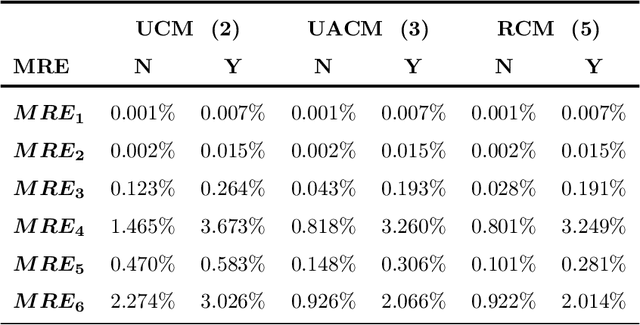
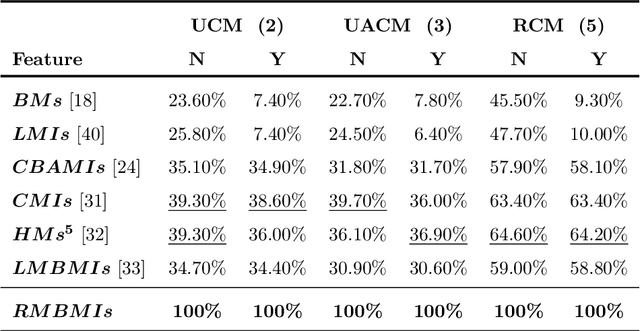
With the development of data acquisition technology, multi-channel data is collected and widely used in many fields. Most of them can be expressed as various types of vector functions. Feature extraction of vector functions for identifying certain patterns of interest is a critical but challenging task. In this paper, we focus on constructing moment invariants of general vector functions. Specifically, we define rotation-affine transform to describe real deformations of general vector functions, and then design a structural frame to systematically generate Gaussian-Hermite moment invariants to this transform model. This is the first time that a uniform frame has been proposed in the literature to construct orthogonal moment invariants of general vector functions. Given a certain type of multi-channel data, we demonstrate how to utilize the new method to derive all possible invariants and to eliminate various dependences among them. For RGB images, 2D and 3D flow fields, we obtain the complete and independent sets of the invariants with low orders and low degrees. Based on synthetic and popular datasets of vector-valued data, the experiments are carried out to evaluate the stability and discriminability of these invariants, and also their robustness to noise. The results clearly show that the moment invariants proposed in our paper have better performance than other previously used moment invariants of vector functions in RGB image classification, vortex detection in 2D vector fields and template matching for 3D flow fields.

Spatio-Temporal Dual Affine Differential Invariant for Skeleton-based Action Recognition

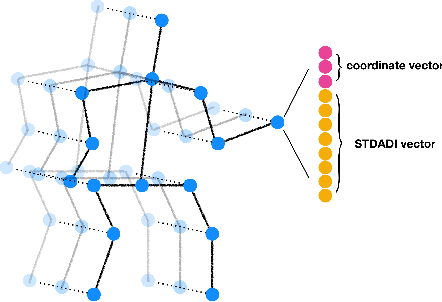
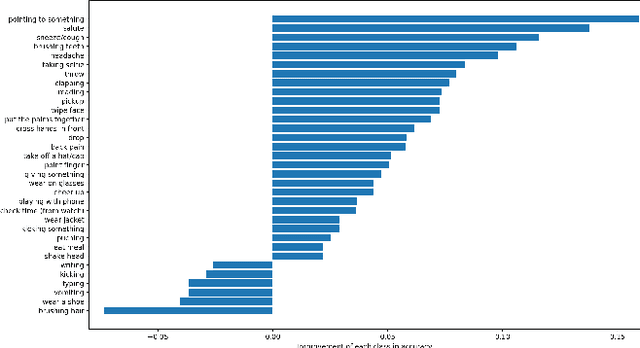
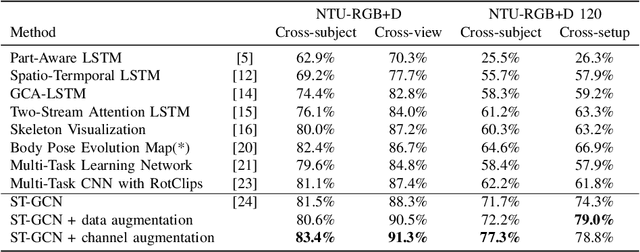
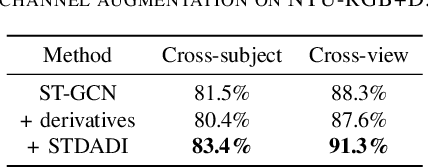
The dynamics of human skeletons have significant information for the task of action recognition. The similarity between trajectories of corresponding joints is an indicating feature of the same action, while this similarity may subject to some distortions that can be modeled as the combination of spatial and temporal affine transformations. In this work, we propose a novel feature called spatio-temporal dual affine differential invariant (STDADI). Furthermore, in order to improve the generalization ability of neural networks, a channel augmentation method is proposed. On the large scale action recognition dataset NTU-RGB+D, and its extended version NTU-RGB+D 120, it achieves remarkable improvements over previous state-of-the-art methods.

Dual affine moment invariants

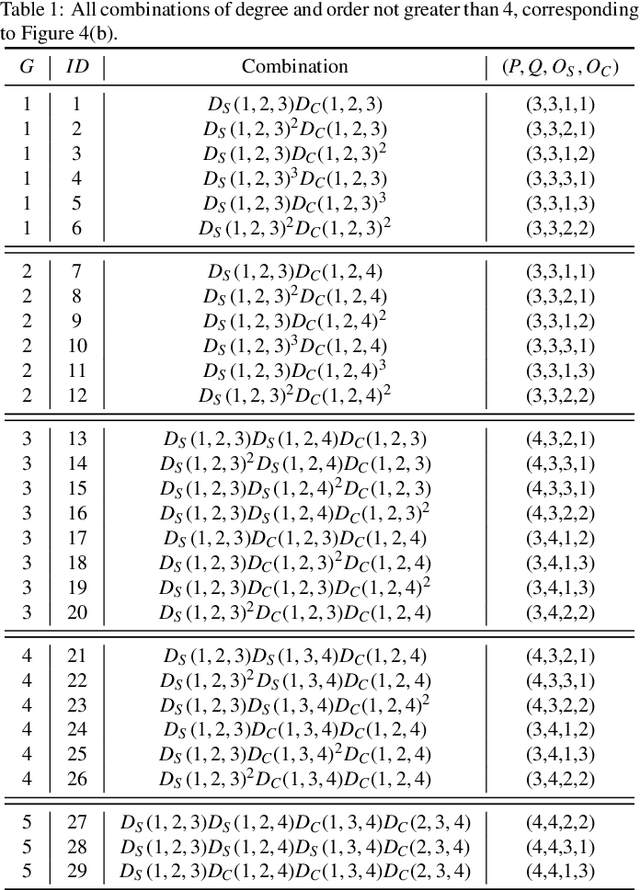
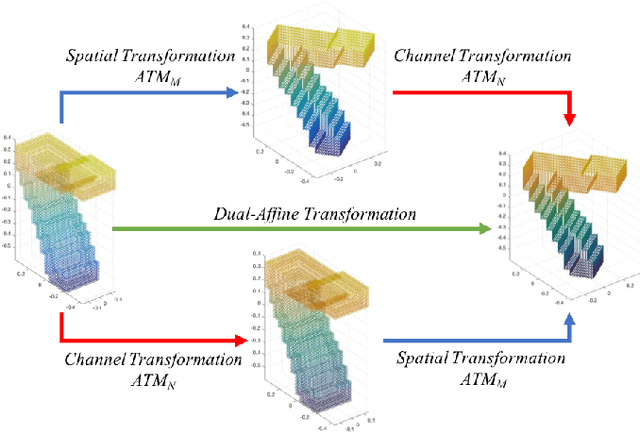
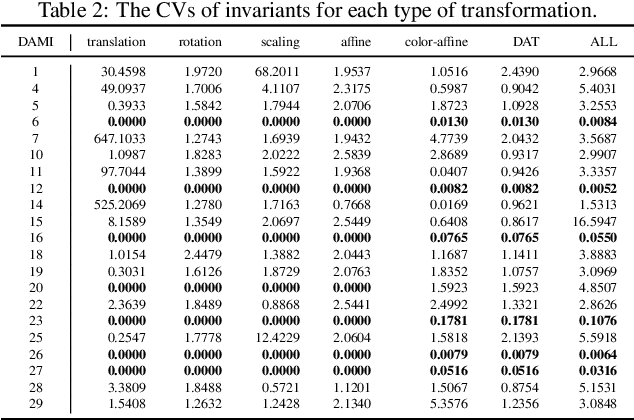
Affine transformation is one of the most common transformations in nature, which is an important issue in the field of computer vision and shape analysis. And affine transformations often occur in both shape and color space simultaneously, which can be termed as Dual-Affine Transformation (DAT). In general, we should derive invariants of different data formats separately, such as 2D color images, 3D color objects, or even higher-dimensional data. To the best of our knowledge, there is no general framework to derive invariants for all of these data formats. In this paper, we propose a general framework to derive moment invariants under DAT for objects in M-dimensional space with N channels, which can be called dual-affine moment invariants (DAMI). Following this framework, we present the generating formula of DAMI under DAT for 3D color objects. Then, we instantiated a complete set of DAMI for 3D color objects with orders and degrees no greater than 4. Finally, we analyze the characteristic of these DAMI and conduct classification experiments to evaluate the stability and discriminability of them. The results prove that DAMI is robust for DAT. Our derivation framework can be applied to data in any dimension with any number of channels.

Image Differential Invariants

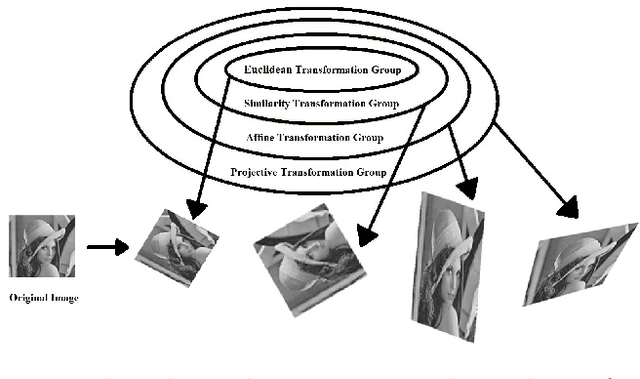
Inspired by the methods of systematic derivation of image moment invariants, we design two fundamental differential operators to generate image differential invariants for the action of 2D Euclidean, similarity and affine transformation groups. Each differential invariant obtained by using the new method can be expressed as a homogeneous polynomial of image partial derivatives. When setting the degree of the polynomial and the order of image partial derivatives are less than or equal to 4, we generate all Euclidean differential invariants and discuss the independence of them in detail. In the experimental part, we find the relation between Euclidean differential invariants and Gaussian-Hermite moment invariants when using the derivatives of Gaussian to estimate image partial derivatives. Texture classification and image patch verification are carried out on some synthetic and popular real databases. We mainly evaluate the stability and discriminability of Euclidean differential invariants and analyse the effects of various factors on performance of them. The experimental results validate image Euclidean differential invariants have better performance than some commonly used local image features in most cases.

Differential and integral invariants under Mobius transformation

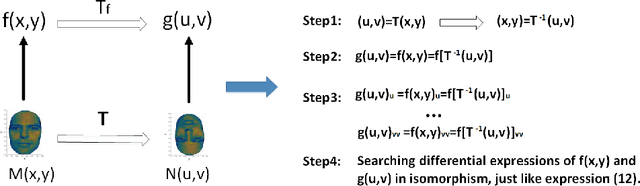
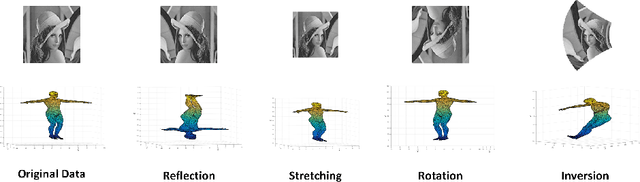
One of the most challenging problems in the domain of 2-D image or 3-D shape is to handle the non-rigid deformation. From the perspective of transformation groups, the conformal transformation is a key part of the diffeomorphism. According to the Liouville Theorem, an important part of the conformal transformation is the Mobius transformation, so we focus on Mobius transformation and propose two differential expressions that are invariable under 2-D and 3-D Mobius transformation respectively. Next, we analyze the absoluteness and relativity of invariance on them and their components. After that, we propose integral invariants under Mobius transformation based on the two differential expressions. Finally, we propose a conjecture about the structure of differential invariants under conformal transformation according to our observation on the composition of the above two differential invariants.

Fast and Efficient Calculations of Structural Invariants of Chirality

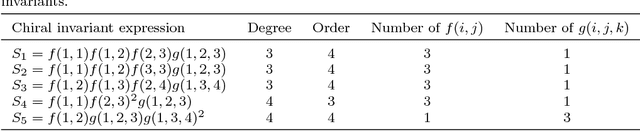
Chirality plays an important role in physics, chemistry, biology, and other fields. It describes an essential symmetry in structure. However, chirality invariants are usually complicated in expression or difficult to evaluate. In this paper, we present five general three-dimensional chirality invariants based on the generating functions. And the five chiral invariants have four characteristics:(1) They play an important role in the detection of symmetry, especially in the treatment of 'false zero' problem. (2) Three of the five chiral invariants decode an universal chirality index. (3) Three of them are proposed for the first time. (4) The five chiral invariants have low order no bigger than 4, brief expression, low time complexity O(n) and can act as descriptors of three-dimensional objects in shape analysis. The five chiral invariants give a geometric view to study the chiral invariants. And the experiments show that the five chirality invariants are effective and efficient, they can be used as a tool for symmetry detection or features in shape analysis.