Dual affine moment invariants
Paper and Code
Nov 19, 2019
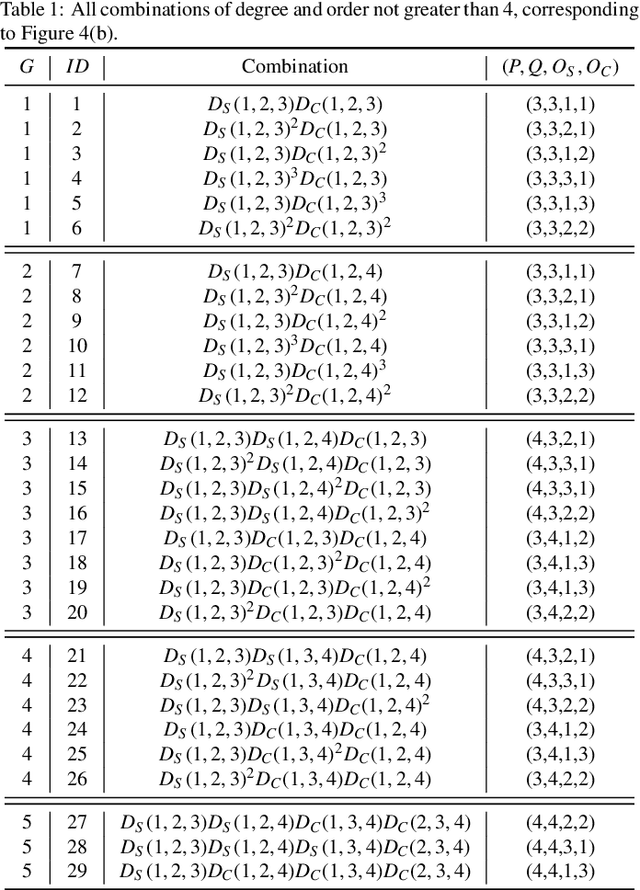
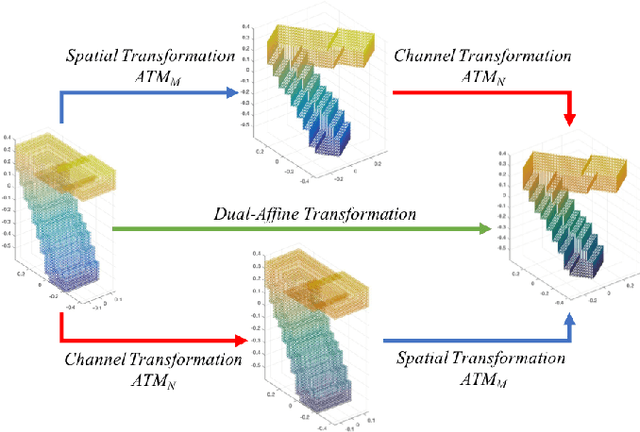
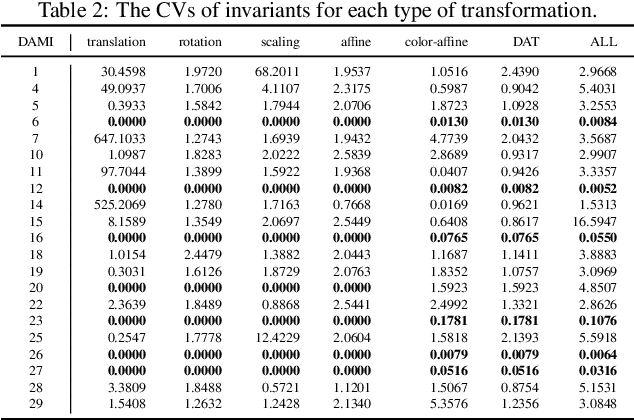
Affine transformation is one of the most common transformations in nature, which is an important issue in the field of computer vision and shape analysis. And affine transformations often occur in both shape and color space simultaneously, which can be termed as Dual-Affine Transformation (DAT). In general, we should derive invariants of different data formats separately, such as 2D color images, 3D color objects, or even higher-dimensional data. To the best of our knowledge, there is no general framework to derive invariants for all of these data formats. In this paper, we propose a general framework to derive moment invariants under DAT for objects in M-dimensional space with N channels, which can be called dual-affine moment invariants (DAMI). Following this framework, we present the generating formula of DAMI under DAT for 3D color objects. Then, we instantiated a complete set of DAMI for 3D color objects with orders and degrees no greater than 4. Finally, we analyze the characteristic of these DAMI and conduct classification experiments to evaluate the stability and discriminability of them. The results prove that DAMI is robust for DAT. Our derivation framework can be applied to data in any dimension with any number of channels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge