Differential and integral invariants under Mobius transformation
Paper and Code
Aug 30, 2018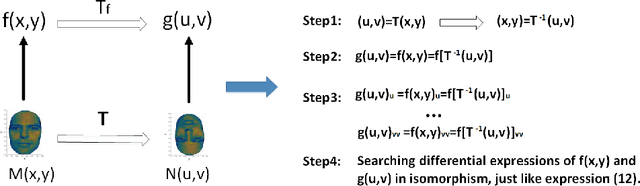

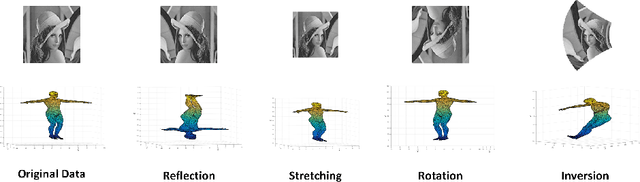

One of the most challenging problems in the domain of 2-D image or 3-D shape is to handle the non-rigid deformation. From the perspective of transformation groups, the conformal transformation is a key part of the diffeomorphism. According to the Liouville Theorem, an important part of the conformal transformation is the Mobius transformation, so we focus on Mobius transformation and propose two differential expressions that are invariable under 2-D and 3-D Mobius transformation respectively. Next, we analyze the absoluteness and relativity of invariance on them and their components. After that, we propose integral invariants under Mobius transformation based on the two differential expressions. Finally, we propose a conjecture about the structure of differential invariants under conformal transformation according to our observation on the composition of the above two differential invariants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge