Image Differential Invariants

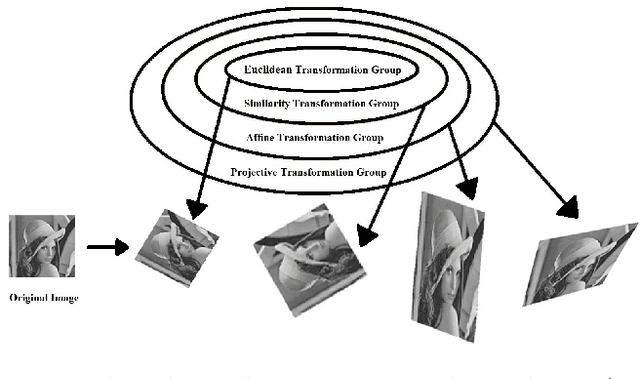
Inspired by the methods of systematic derivation of image moment invariants, we design two fundamental differential operators to generate image differential invariants for the action of 2D Euclidean, similarity and affine transformation groups. Each differential invariant obtained by using the new method can be expressed as a homogeneous polynomial of image partial derivatives. When setting the degree of the polynomial and the order of image partial derivatives are less than or equal to 4, we generate all Euclidean differential invariants and discuss the independence of them in detail. In the experimental part, we find the relation between Euclidean differential invariants and Gaussian-Hermite moment invariants when using the derivatives of Gaussian to estimate image partial derivatives. Texture classification and image patch verification are carried out on some synthetic and popular real databases. We mainly evaluate the stability and discriminability of Euclidean differential invariants and analyse the effects of various factors on performance of them. The experimental results validate image Euclidean differential invariants have better performance than some commonly used local image features in most cases.