Gaussian-Hermite Moment Invariants of General Vector Functions to Rotation-Affine Transform

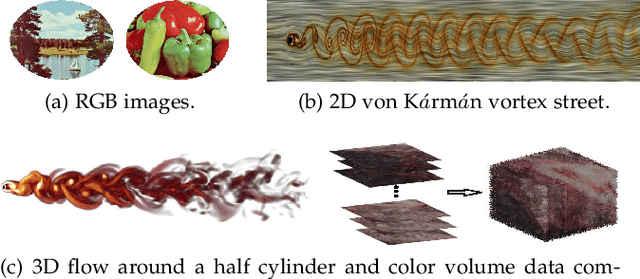
With the development of data acquisition technology, multi-channel data is collected and widely used in many fields. Most of them can be expressed as various types of vector functions. Feature extraction of vector functions for identifying certain patterns of interest is a critical but challenging task. In this paper, we focus on constructing moment invariants of general vector functions. Specifically, we define rotation-affine transform to describe real deformations of general vector functions, and then design a structural frame to systematically generate Gaussian-Hermite moment invariants to this transform model. This is the first time that a uniform frame has been proposed in the literature to construct orthogonal moment invariants of general vector functions. Given a certain type of multi-channel data, we demonstrate how to utilize the new method to derive all possible invariants and to eliminate various dependences among them. For RGB images, 2D and 3D flow fields, we obtain the complete and independent sets of the invariants with low orders and low degrees. Based on synthetic and popular datasets of vector-valued data, the experiments are carried out to evaluate the stability and discriminability of these invariants, and also their robustness to noise. The results clearly show that the moment invariants proposed in our paper have better performance than other previously used moment invariants of vector functions in RGB image classification, vortex detection in 2D vector fields and template matching for 3D flow fields.