MDDD: Manifold-based Domain Adaptation with Dynamic Distribution for Non-Deep Transfer Learning in Cross-subject and Cross-session EEG-based Emotion Recognition

Emotion decoding using Electroencephalography (EEG)-based affective brain-computer interfaces represents a significant area within the field of affective computing. In the present study, we propose a novel non-deep transfer learning method, termed as Manifold-based Domain adaptation with Dynamic Distribution (MDDD). The proposed MDDD includes four main modules: manifold feature transformation, dynamic distribution alignment, classifier learning, and ensemble learning. The data undergoes a transformation onto an optimal Grassmann manifold space, enabling dynamic alignment of the source and target domains. This process prioritizes both marginal and conditional distributions according to their significance, ensuring enhanced adaptation efficiency across various types of data. In the classifier learning, the principle of structural risk minimization is integrated to develop robust classification models. This is complemented by dynamic distribution alignment, which refines the classifier iteratively. Additionally, the ensemble learning module aggregates the classifiers obtained at different stages of the optimization process, which leverages the diversity of the classifiers to enhance the overall prediction accuracy. The experimental results indicate that MDDD outperforms traditional non-deep learning methods, achieving an average improvement of 3.54%, and is comparable to deep learning methods. This suggests that MDDD could be a promising method for enhancing the utility and applicability of aBCIs in real-world scenarios.

Sparse estimation via $\ell_q$ optimization method in high-dimensional linear regression

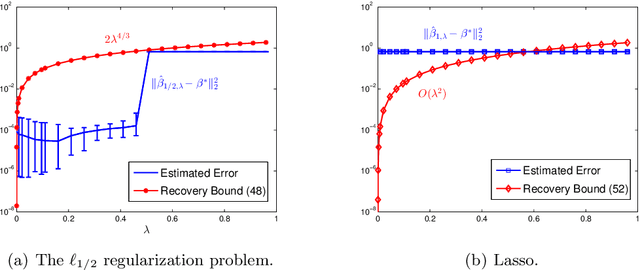
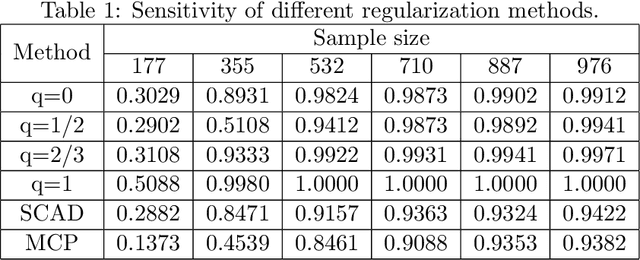
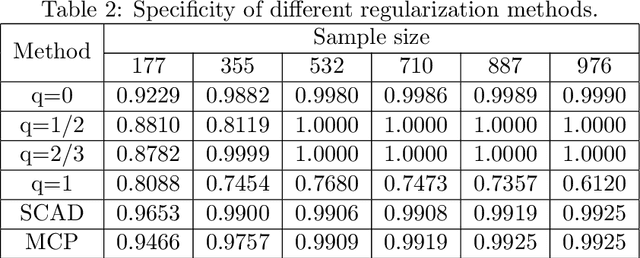
In this paper, we discuss the statistical properties of the $\ell_q$ optimization methods $(0<q\leq 1)$, including the $\ell_q$ minimization method and the $\ell_q$ regularization method, for estimating a sparse parameter from noisy observations in high-dimensional linear regression with either a deterministic or random design. For this purpose, we introduce a general $q$-restricted eigenvalue condition (REC) and provide its sufficient conditions in terms of several widely-used regularity conditions such as sparse eigenvalue condition, restricted isometry property, and mutual incoherence property. By virtue of the $q$-REC, we exhibit the stable recovery property of the $\ell_q$ optimization methods for either deterministic or random designs by showing that the $\ell_2$ recovery bound $O(\epsilon^2)$ for the $\ell_q$ minimization method and the oracle inequality and $\ell_2$ recovery bound $O(\lambda^{\frac{2}{2-q}}s)$ for the $\ell_q$ regularization method hold respectively with high probability. The results in this paper are nonasymptotic and only assume the weak $q$-REC. The preliminary numerical results verify the established statistical property and demonstrate the advantages of the $\ell_q$ regularization method over some existing sparse optimization methods.

Nonconvex and Nonsmooth Sparse Optimization via Adaptively Iterative Reweighted Methods

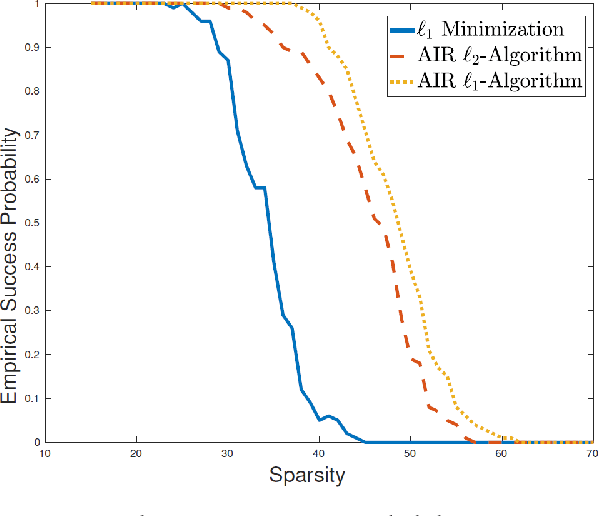
We present a general formulation of nonconvex and nonsmooth sparse optimization problems with a convexset constraint, which takes into account most existing types of nonconvex sparsity-inducing terms. It thus brings strong applicability to a wide range of applications. We further design a general algorithmic framework of adaptively iterative reweighted algorithms for solving the nonconvex and nonsmooth sparse optimization problems. This is achieved by solving a sequence of weighted convex penalty subproblems with adaptively updated weights. The first-order optimality condition is then derived and the global convergence results are provided under loose assumptions. This makes our theoretical results a practical tool for analyzing a family of various iteratively reweighted algorithms. In particular, for the iteratively reweighed $\ell_1$-algorithm, global convergence analysis is provided for cases with diminishing relaxation parameter. For the iteratively reweighed $\ell_2$-algorithm, adaptively decreasing relaxation parameter is applicable and the existence of the cluster point to the algorithm is established. The effectiveness and efficiency of our proposed formulation and the algorithms are demonstrated in numerical experiments in various sparse optimization problems.