Out-of-distribution Detection in Medical Image Analysis: A survey

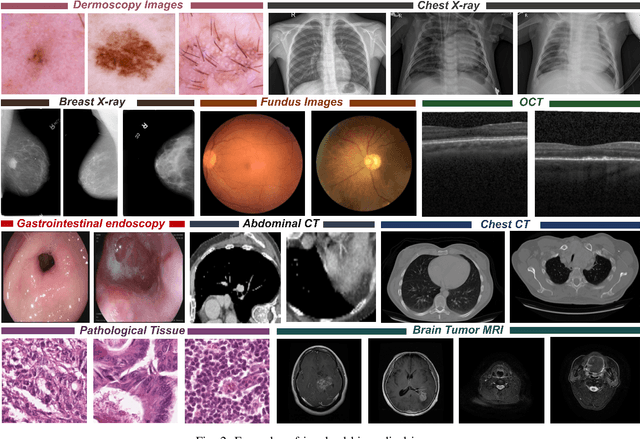
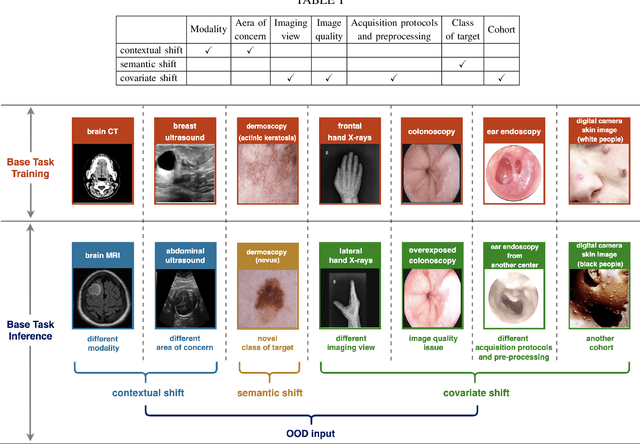
Computer-aided diagnostics has benefited from the development of deep learning-based computer vision techniques in these years. Traditional supervised deep learning methods assume that the test sample is drawn from the identical distribution as the training data. However, it is possible to encounter out-of-distribution samples in real-world clinical scenarios, which may cause silent failure in deep learning-based medical image analysis tasks. Recently, research has explored various out-of-distribution (OOD) detection situations and techniques to enable a trustworthy medical AI system. In this survey, we systematically review the recent advances in OOD detection in medical image analysis. We first explore several factors that may cause a distributional shift when using a deep-learning-based model in clinic scenarios, with three different types of distributional shift well defined on top of these factors. Then a framework is suggested to categorize and feature existing solutions, while the previous studies are reviewed based on the methodology taxonomy. Our discussion also includes evaluation protocols and metrics, as well as the challenge and a research direction lack of exploration.

Sparse estimation via $\ell_q$ optimization method in high-dimensional linear regression

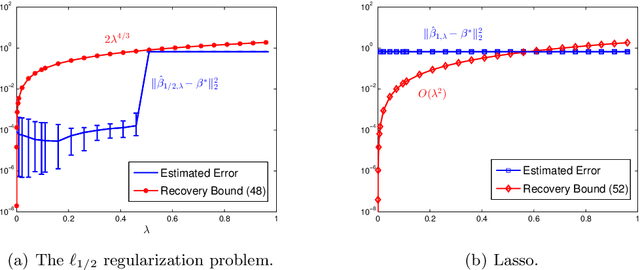
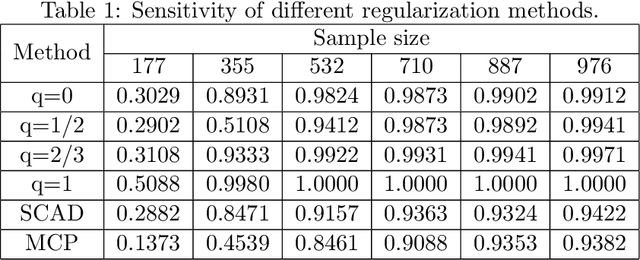
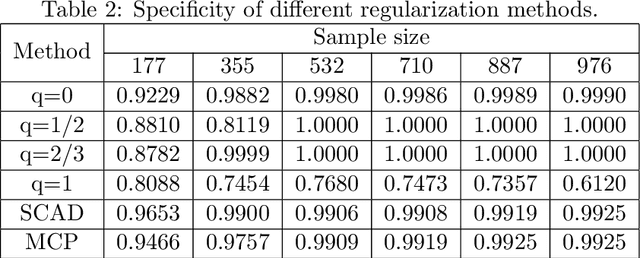
In this paper, we discuss the statistical properties of the $\ell_q$ optimization methods $(0<q\leq 1)$, including the $\ell_q$ minimization method and the $\ell_q$ regularization method, for estimating a sparse parameter from noisy observations in high-dimensional linear regression with either a deterministic or random design. For this purpose, we introduce a general $q$-restricted eigenvalue condition (REC) and provide its sufficient conditions in terms of several widely-used regularity conditions such as sparse eigenvalue condition, restricted isometry property, and mutual incoherence property. By virtue of the $q$-REC, we exhibit the stable recovery property of the $\ell_q$ optimization methods for either deterministic or random designs by showing that the $\ell_2$ recovery bound $O(\epsilon^2)$ for the $\ell_q$ minimization method and the oracle inequality and $\ell_2$ recovery bound $O(\lambda^{\frac{2}{2-q}}s)$ for the $\ell_q$ regularization method hold respectively with high probability. The results in this paper are nonasymptotic and only assume the weak $q$-REC. The preliminary numerical results verify the established statistical property and demonstrate the advantages of the $\ell_q$ regularization method over some existing sparse optimization methods.