Tianzi Jiang
Neural Proteomics Fields for Super-resolved Spatial Proteomics Prediction
Aug 24, 2025Abstract:Spatial proteomics maps protein distributions in tissues, providing transformative insights for life sciences. However, current sequencing-based technologies suffer from low spatial resolution, and substantial inter-tissue variability in protein expression further compromises the performance of existing molecular data prediction methods. In this work, we introduce the novel task of spatial super-resolution for sequencing-based spatial proteomics (seq-SP) and, to the best of our knowledge, propose the first deep learning model for this task--Neural Proteomics Fields (NPF). NPF formulates seq-SP as a protein reconstruction problem in continuous space by training a dedicated network for each tissue. The model comprises a Spatial Modeling Module, which learns tissue-specific protein spatial distributions, and a Morphology Modeling Module, which extracts tissue-specific morphological features. Furthermore, to facilitate rigorous evaluation, we establish an open-source benchmark dataset, Pseudo-Visium SP, for this task. Experimental results demonstrate that NPF achieves state-of-the-art performance with fewer learnable parameters, underscoring its potential for advancing spatial proteomics research. Our code and dataset are publicly available at https://github.com/Bokai-Zhao/NPF.
Digital twin brain: a bridge between biological intelligence and artificial intelligence
Aug 03, 2023Abstract:In recent years, advances in neuroscience and artificial intelligence have paved the way for unprecedented opportunities for understanding the complexity of the brain and its emulation by computational systems. Cutting-edge advancements in neuroscience research have revealed the intricate relationship between brain structure and function, while the success of artificial neural networks highlights the importance of network architecture. Now is the time to bring them together to better unravel how intelligence emerges from the brain's multiscale repositories. In this review, we propose the Digital Twin Brain (DTB) as a transformative platform that bridges the gap between biological and artificial intelligence. It consists of three core elements: the brain structure that is fundamental to the twinning process, bottom-layer models to generate brain functions, and its wide spectrum of applications. Crucially, brain atlases provide a vital constraint, preserving the brain's network organization within the DTB. Furthermore, we highlight open questions that invite joint efforts from interdisciplinary fields and emphasize the far-reaching implications of the DTB. The DTB can offer unprecedented insights into the emergence of intelligence and neurological disorders, which holds tremendous promise for advancing our understanding of both biological and artificial intelligence, and ultimately propelling the development of artificial general intelligence and facilitating precision mental healthcare.
Sparse estimation via $\ell_q$ optimization method in high-dimensional linear regression
Nov 12, 2019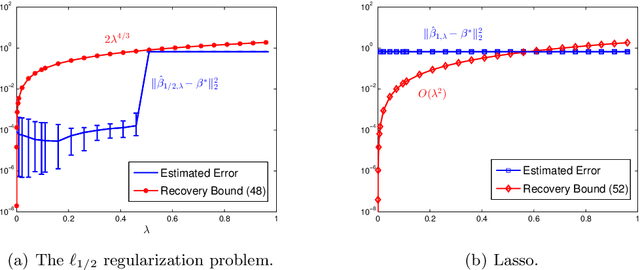
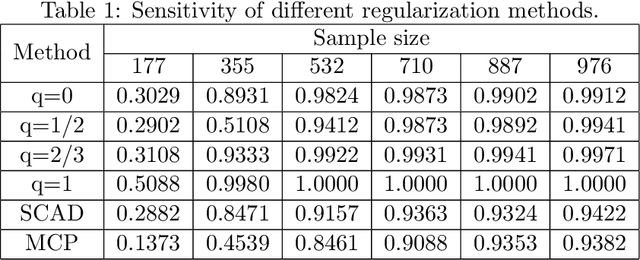
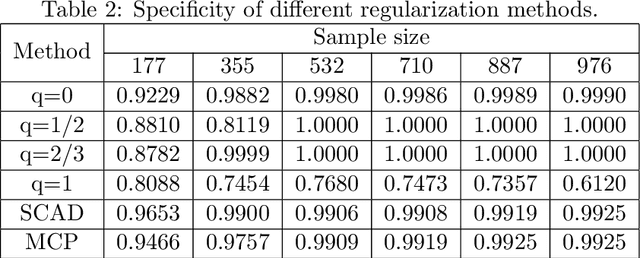
Abstract:In this paper, we discuss the statistical properties of the $\ell_q$ optimization methods $(0<q\leq 1)$, including the $\ell_q$ minimization method and the $\ell_q$ regularization method, for estimating a sparse parameter from noisy observations in high-dimensional linear regression with either a deterministic or random design. For this purpose, we introduce a general $q$-restricted eigenvalue condition (REC) and provide its sufficient conditions in terms of several widely-used regularity conditions such as sparse eigenvalue condition, restricted isometry property, and mutual incoherence property. By virtue of the $q$-REC, we exhibit the stable recovery property of the $\ell_q$ optimization methods for either deterministic or random designs by showing that the $\ell_2$ recovery bound $O(\epsilon^2)$ for the $\ell_q$ minimization method and the oracle inequality and $\ell_2$ recovery bound $O(\lambda^{\frac{2}{2-q}}s)$ for the $\ell_q$ regularization method hold respectively with high probability. The results in this paper are nonasymptotic and only assume the weak $q$-REC. The preliminary numerical results verify the established statistical property and demonstrate the advantages of the $\ell_q$ regularization method over some existing sparse optimization methods.
Regularized Spherical Polar Fourier Diffusion MRI with Optimal Dictionary Learning
Jul 02, 2013
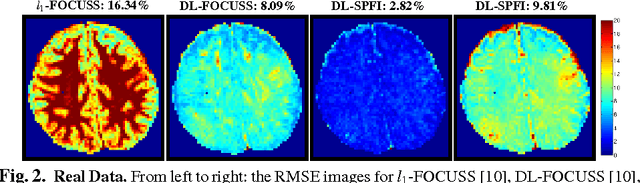
Abstract:Compressed Sensing (CS) takes advantage of signal sparsity or compressibility and allows superb signal reconstruction from relatively few measurements. Based on CS theory, a suitable dictionary for sparse representation of the signal is required. In diffusion MRI (dMRI), CS methods were proposed to reconstruct diffusion-weighted signal and the Ensemble Average Propagator (EAP), and there are two kinds of Dictionary Learning (DL) methods: 1) Discrete Representation DL (DR-DL), and 2) Continuous Representation DL (CR-DL). DR-DL is susceptible to numerical inaccuracy owing to interpolation and regridding errors in a discretized q-space. In this paper, we propose a novel CR-DL approach, called Dictionary Learning - Spherical Polar Fourier Imaging (DL-SPFI) for effective compressed-sensing reconstruction of the q-space diffusion-weighted signal and the EAP. In DL-SPFI, an dictionary that sparsifies the signal is learned from the space of continuous Gaussian diffusion signals. The learned dictionary is then adaptively applied to different voxels using a weighted LASSO framework for robust signal reconstruction. The adaptive dictionary is proved to be optimal. Compared with the start-of-the-art CR-DL and DR-DL methods proposed by Merlet et al. and Bilgic et al., espectively, our work offers the following advantages. First, the learned dictionary is proved to be optimal for Gaussian diffusion signals. Second, to our knowledge, this is the first work to learn a voxel-adaptive dictionary. The importance of the adaptive dictionary in EAP reconstruction will be demonstrated theoretically and empirically. Third, optimization in DL-SPFI is only performed in a small subspace resided by the SPF coefficients, as opposed to the q-space approach utilized by Merlet et al. The experiment results demonstrate the advantages of DL-SPFI over the original SPF basis and Bilgic et al.'s method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge