Sparse estimation via $\ell_q$ optimization method in high-dimensional linear regression
Paper and Code
Nov 12, 2019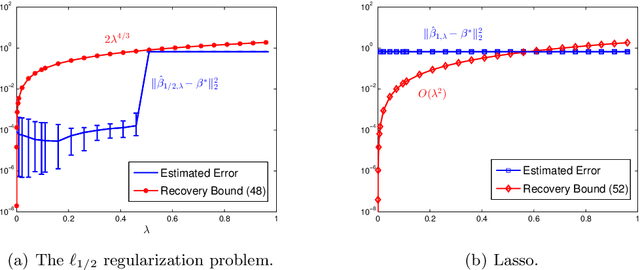
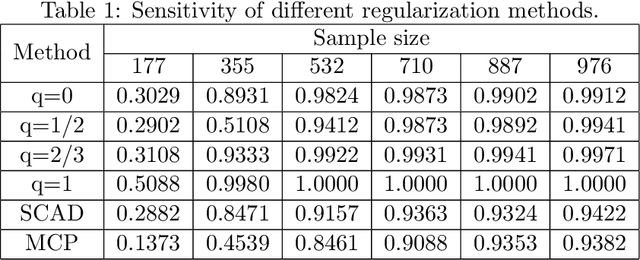
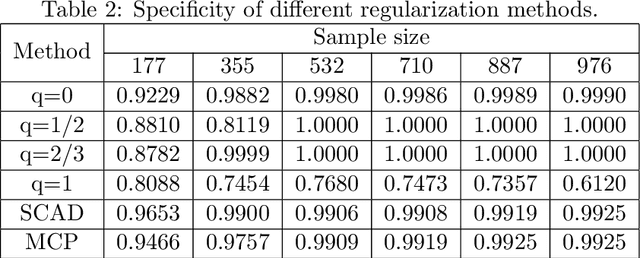
In this paper, we discuss the statistical properties of the $\ell_q$ optimization methods $(0<q\leq 1)$, including the $\ell_q$ minimization method and the $\ell_q$ regularization method, for estimating a sparse parameter from noisy observations in high-dimensional linear regression with either a deterministic or random design. For this purpose, we introduce a general $q$-restricted eigenvalue condition (REC) and provide its sufficient conditions in terms of several widely-used regularity conditions such as sparse eigenvalue condition, restricted isometry property, and mutual incoherence property. By virtue of the $q$-REC, we exhibit the stable recovery property of the $\ell_q$ optimization methods for either deterministic or random designs by showing that the $\ell_2$ recovery bound $O(\epsilon^2)$ for the $\ell_q$ minimization method and the oracle inequality and $\ell_2$ recovery bound $O(\lambda^{\frac{2}{2-q}}s)$ for the $\ell_q$ regularization method hold respectively with high probability. The results in this paper are nonasymptotic and only assume the weak $q$-REC. The preliminary numerical results verify the established statistical property and demonstrate the advantages of the $\ell_q$ regularization method over some existing sparse optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge