Nonconvex and Nonsmooth Sparse Optimization via Adaptively Iterative Reweighted Methods

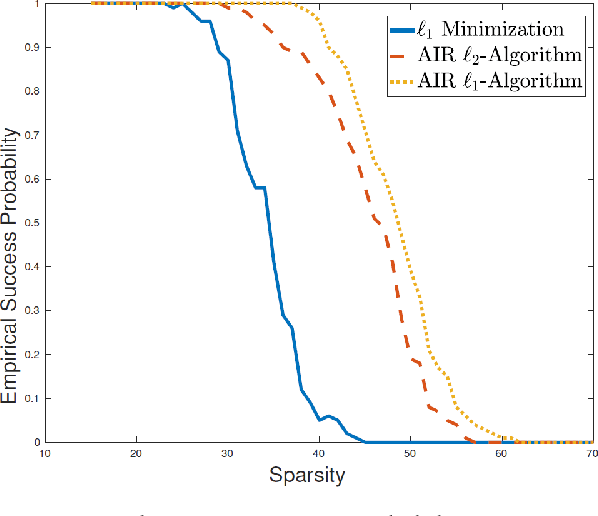
We present a general formulation of nonconvex and nonsmooth sparse optimization problems with a convexset constraint, which takes into account most existing types of nonconvex sparsity-inducing terms. It thus brings strong applicability to a wide range of applications. We further design a general algorithmic framework of adaptively iterative reweighted algorithms for solving the nonconvex and nonsmooth sparse optimization problems. This is achieved by solving a sequence of weighted convex penalty subproblems with adaptively updated weights. The first-order optimality condition is then derived and the global convergence results are provided under loose assumptions. This makes our theoretical results a practical tool for analyzing a family of various iteratively reweighted algorithms. In particular, for the iteratively reweighed $\ell_1$-algorithm, global convergence analysis is provided for cases with diminishing relaxation parameter. For the iteratively reweighed $\ell_2$-algorithm, adaptively decreasing relaxation parameter is applicable and the existence of the cluster point to the algorithm is established. The effectiveness and efficiency of our proposed formulation and the algorithms are demonstrated in numerical experiments in various sparse optimization problems.