Hierarchical Adaptive Eviction for KV Cache Management in Multimodal Language Models

The integration of visual information into Large Language Models (LLMs) has enabled Multimodal LLMs (MLLMs), but the quadratic memory and computational costs of Transformer architectures remain a bottleneck. Existing KV cache eviction strategies fail to address the heterogeneous attention distributions between visual and text tokens, leading to suboptimal efficiency or degraded performance. In this paper, we propose Hierarchical Adaptive Eviction (HAE), a KV cache eviction framework that optimizes text-visual token interaction in MLLMs by implementing Dual-Attention Pruning during pre-filling (leveraging visual token sparsity and attention variance) and a Dynamic Decoding Eviction Strategy (inspired by OS Recycle Bins) during decoding. HAE minimizes KV cache usage across layers, reduces computational overhead via index broadcasting, and theoretically ensures superior information integrity and lower error bounds compared to greedy strategies, enhancing efficiency in both comprehension and generation tasks. Empirically, HAE reduces KV-Cache memory by 41\% with minimal accuracy loss (0.3\% drop) in image understanding tasks and accelerates story generation inference by 1.5x while maintaining output quality on Phi3.5-Vision-Instruct model.

ARCQuant: Boosting NVFP4 Quantization with Augmented Residual Channels for LLMs

The emergence of fine-grained numerical formats like NVFP4 presents new opportunities for efficient Large Language Model (LLM) inference. However, it is difficult to adapt existing Post-Training Quantization (PTQ) strategies to these formats: rotation-based methods compromise fine-grained block isolation; smoothing techniques struggle with significant 4-bit quantization errors; and mixed-precision approaches often conflict with hardware constraints on unified-precision computation. To address these challenges, we propose ARCQuant, a framework that boosts NVFP4 performance via Augmented Residual Channels. Distinct from methods that compromise block isolation or hardware uniformity, ARCQuant maintains a strictly unified NVFP4 format by augmenting the activation matrix with quantized residual channels. This design integrates the error compensation process directly into the matrix reduction dimension, enabling the use of standard, highly optimized GEMM kernels with minimal overhead. Theoretical analysis confirms that the worst-case error bound of our dual-stage NVFP4 quantization is comparable to that of standard 8-bit formats such as MXFP8. Extensive experiments on LLaMA and Qwen models demonstrate that ARCQuant achieves state-of-the-art accuracy, comparable to full-precision baselines in perplexity and downstream tasks. Furthermore, deployment on RTX 5090 and RTX PRO 6000 GPUs confirms practical benefits, achieving up to 3x speedup over FP16. Our code is available at https://github.com/actypedef/ARCQuant .

SEE: Sememe Entanglement Encoding for Transformer-bases Models Compression

Transformer-based large language models exhibit groundbreaking capabilities, but their storage and computational costs are prohibitively high, limiting their application in resource-constrained scenarios. An effective approach is to eliminate redundant model parameters and computational costs while incorporating efficient expert-derived knowledge structures to achieve a balance between compression and performance. Therefore, we propose the \textit{Sememe Entanglement Encoding (SEE)} algorithm. Guided by expert prior knowledge, the model is compressed through the low-rank approximation idea. In Entanglement Embedding, basic semantic units such as sememes are represented as low-dimensional vectors, and then reconstructed into high-dimensional word embeddings through the combination of generalized quantum entanglement. We adapt the Sememe Entanglement Encoding algorithm to transformer-based models of different magnitudes. Experimental results indicate that our approach achieves stable performance while compressing model parameters and computational costs.

CrossQuant: A Post-Training Quantization Method with Smaller Quantization Kernel for Precise Large Language Model Compression

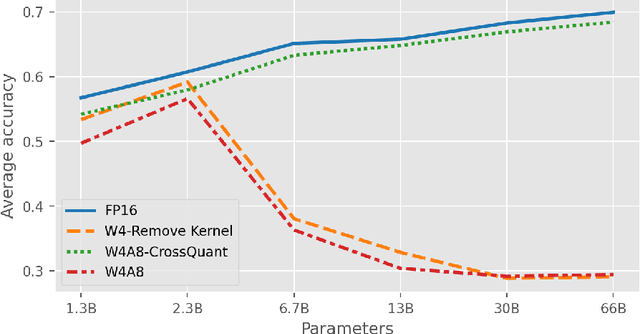
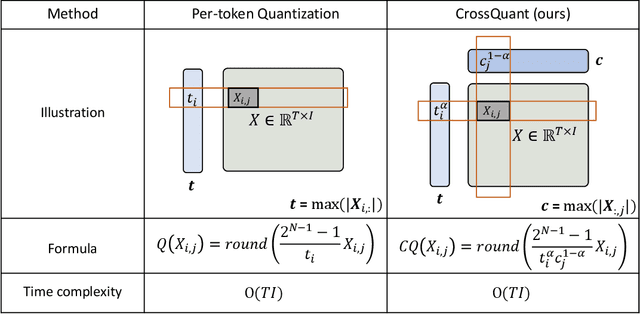
Post-Training Quantization (PTQ) is an effective technique for compressing Large Language Models (LLMs). While many studies focus on quantizing both weights and activations, it is still a challenge to maintain the accuracy of LLM after activating quantization. To investigate the primary cause, we extend the concept of kernel from linear algebra to quantization functions to define a new term, "quantization kernel", which refers to the set of elements in activations that are quantized to zero. Through quantitative analysis of the quantization kernel, we find that these elements are crucial for maintaining the accuracy of quantized LLMs. With the decrease of quantization kernel, the precision of quantized LLMs increases. If the quantization kernel proportion is kept below 19% for OPT models and below 1% for LLaMA models, the precision loss from quantizing activations to INT8 becomes negligible. Motivated by the goal of developing a quantization method with small quantization kernel, we propose CrossQuant: a simple yet effective method for quantizing activations. CrossQuant cross-quantizes elements using row and column-wise absolute maximum vectors, achieving a quantization kernel of approximately 16% for OPT models and less than 0.1% for LLaMA models. Experimental results on LLMs (LLaMA, OPT) ranging from 6.7B to 70B parameters demonstrate that CrossQuant improves or maintains perplexity and accuracy in language modeling, zero-shot, and few-shot tasks.

3D-RPE: Enhancing Long-Context Modeling Through 3D Rotary Position Encoding

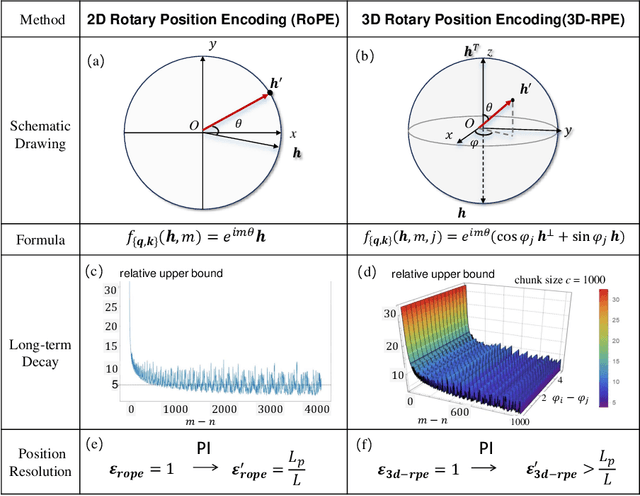
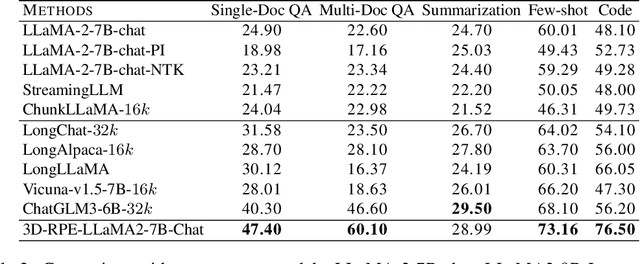
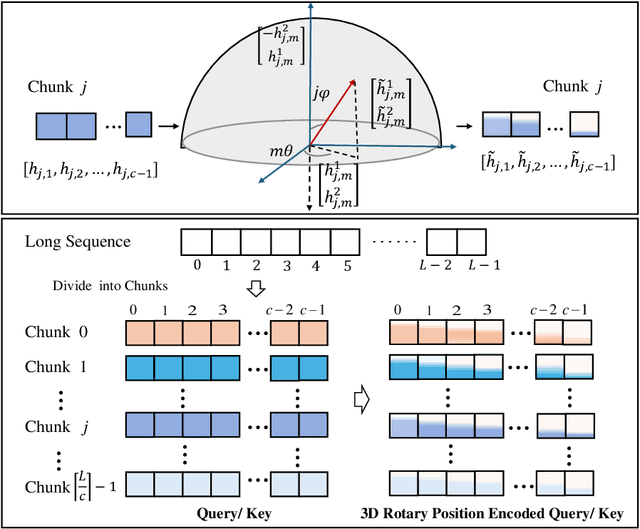
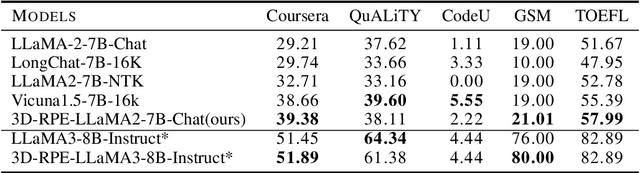
Inspired by the Bloch Sphere representation, we propose a novel rotary position encoding on a three-dimensional sphere, named 3D Rotary Position Encoding (3D-RPE). 3D-RPE is an advanced version of the widely used 2D Rotary Position Encoding (RoPE), with two major advantages for modeling long contexts: controllable long-term decay and improved position resolution. For controllable long-term decay, 3D-RPE allows for the regulation of long-term decay within the chunk size, ensuring the modeling of relative positional information between tokens at a distant relative position. For enhanced position resolution, 3D-RPE can mitigate the degradation of position resolution caused by position interpolation on RoPE. We have conducted experiments on long-context Natural Language Understanding (NLU) and long-sequence Language Modeling (LM) tasks. From the experimental results, 3D-RPE achieved performance improvements over RoPE, especially in long-context NLU tasks.

TensorCoder: Dimension-Wise Attention via Tensor Representation for Natural Language Modeling

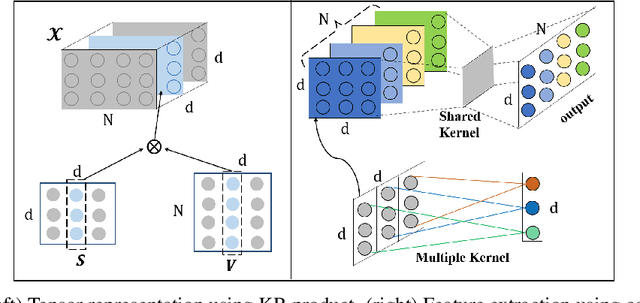
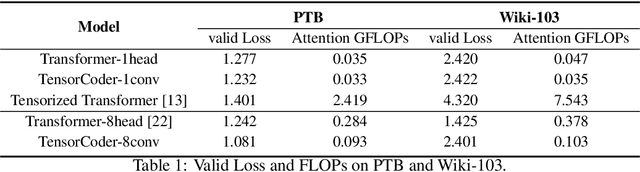
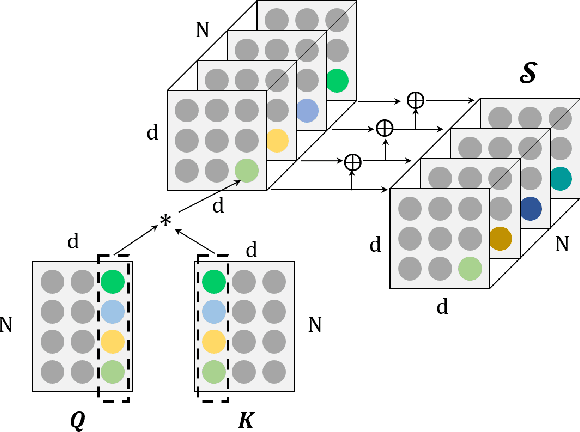
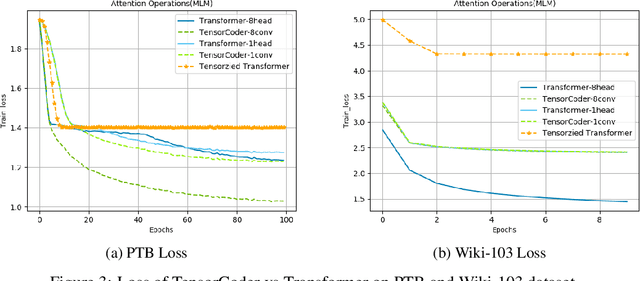
Transformer has been widely-used in many Natural Language Processing (NLP) tasks and the scaled dot-product attention between tokens is a core module of Transformer. This attention is a token-wise design and its complexity is quadratic to the length of sequence, limiting its application potential for long sequence tasks. In this paper, we propose a dimension-wise attention mechanism based on which a novel language modeling approach (namely TensorCoder) can be developed. The dimension-wise attention can reduce the attention complexity from the original $O(N^2d)$ to $O(Nd^2)$, where $N$ is the length of the sequence and $d$ is the dimensionality of head. We verify TensorCoder on two tasks including masked language modeling and neural machine translation. Compared with the original Transformer, TensorCoder not only greatly reduces the calculation of the original model but also obtains improved performance on masked language modeling task (in PTB dataset) and comparable performance on machine translation tasks.

A Tensorized Transformer for Language Modeling

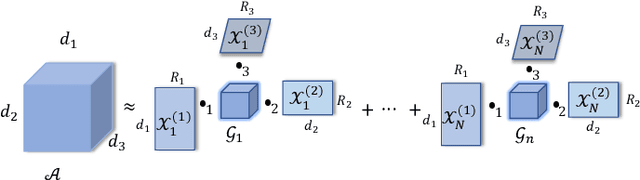
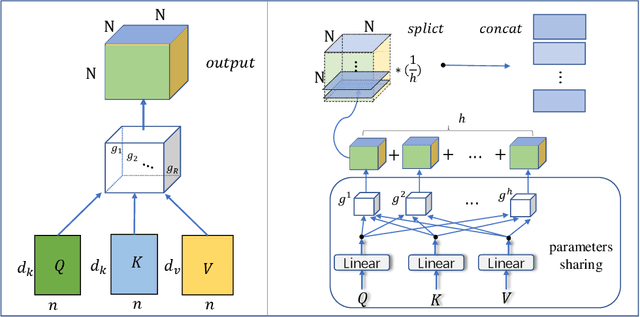
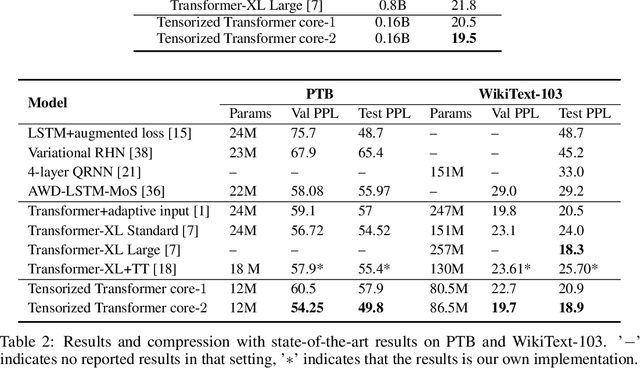
Latest development of neural models has connected the encoder and decoder through a self-attention mechanism. In particular, Transformer, which is solely based on self-attention, has led to breakthroughs in Natural Language Processing (NLP) tasks. However, the multi-head attention mechanism, as a key component of Transformer, limits the effective deployment of the model to a limited resource setting. In this paper, based on the ideas of tensor decomposition and parameters sharing, we propose a novel self-attention model (namely Multi-linear attention) with Block-Term Tensor Decomposition (BTD). We test and verify the proposed attention method on three language modeling tasks (i.e., PTB, WikiText-103 and One-billion) and a neural machine translation task (i.e., WMT-2016 English-German). Multi-linear attention can not only largely compress the model parameters but also obtain performance improvements, compared with a number of language modeling approaches, such as Transformer, Transformer-XL, and Transformer with tensor train decomposition.

A Generalized Language Model in Tensor Space

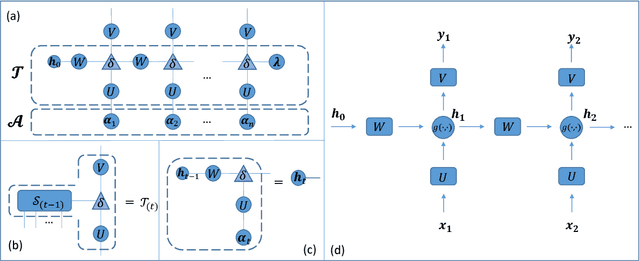
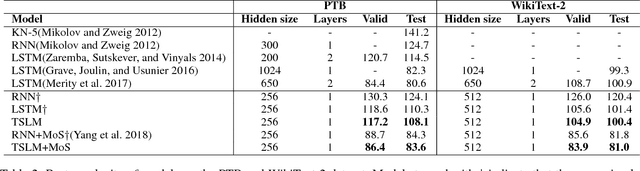
In the literature, tensors have been effectively used for capturing the context information in language models. However, the existing methods usually adopt relatively-low order tensors, which have limited expressive power in modeling language. Developing a higher-order tensor representation is challenging, in terms of deriving an effective solution and showing its generality. In this paper, we propose a language model named Tensor Space Language Model (TSLM), by utilizing tensor networks and tensor decomposition. In TSLM, we build a high-dimensional semantic space constructed by the tensor product of word vectors. Theoretically, we prove that such tensor representation is a generalization of the n-gram language model. We further show that this high-order tensor representation can be decomposed to a recursive calculation of conditional probability for language modeling. The experimental results on Penn Tree Bank (PTB) dataset and WikiText benchmark demonstrate the effectiveness of TSLM.