Multi-State-Action Tokenisation in Decision Transformers for Multi-Discrete Action Spaces

Decision Transformers, in their vanilla form, struggle to perform on image-based environments with multi-discrete action spaces. Although enhanced Decision Transformer architectures have been developed to improve performance, these methods have not specifically addressed this problem of multi-discrete action spaces which hampers existing Decision Transformer architectures from learning good representations. To mitigate this, we propose Multi-State Action Tokenisation (M-SAT), an approach for tokenising actions in multi-discrete action spaces that enhances the model's performance in such environments. Our approach involves two key changes: disentangling actions to the individual action level and tokenising the actions with auxiliary state information. These two key changes also improve individual action level interpretability and visibility within the attention layers. We demonstrate the performance gains of M-SAT on challenging ViZDoom environments with multi-discrete action spaces and image-based state spaces, including the Deadly Corridor and My Way Home scenarios, where M-SAT outperforms the baseline Decision Transformer without any additional data or heavy computational overheads. Additionally, we find that removing positional encoding does not adversely affect M-SAT's performance and, in some cases, even improves it.

Semi-supervised segmentation of land cover images using nonlinear canonical correlation analysis with multiple features and t-SNE

Image segmentation is a clustering task whereby each pixel is assigned a cluster label. Remote sensing data usually consists of multiple bands of spectral images in which there exist semantically meaningful land cover subregions, co-registered with other source data such as LIDAR (LIght Detection And Ranging) data, where available. This suggests that, in order to account for spatial correlation between pixels, a feature vector associated with each pixel may be a vectorized tensor representing the multiple bands and a local patch as appropriate. Similarly, multiple types of texture features based on a pixel's local patch would also be beneficial for encoding locally statistical information and spatial variations, without necessarily labelling pixel-wise a large amount of ground truth, then training a supervised model, which is sometimes impractical. In this work, by resorting to label only a small quantity of pixels, a new semi-supervised segmentation approach is proposed. Initially, over all pixels, an image data matrix is created in high dimensional feature space. Then, t-SNE projects the high dimensional data onto 3D embedding. By using radial basis functions as input features, which use the labelled data samples as centres, to pair with the output class labels, a modified canonical correlation analysis algorithm, referred to as RBF-CCA, is introduced which learns the associated projection matrix via the small labelled data set. The associated canonical variables, obtained for the full image, are applied by k-means clustering algorithm. The proposed semi-supervised RBF-CCA algorithm has been implemented on several remotely sensed multispectral images, demonstrating excellent segmentation results.

Structured Radial Basis Function Network: Modelling Diversity for Multiple Hypotheses Prediction

Multi-modal regression is important in forecasting nonstationary processes or with a complex mixture of distributions. It can be tackled with multiple hypotheses frameworks but with the difficulty of combining them efficiently in a learning model. A Structured Radial Basis Function Network is presented as an ensemble of multiple hypotheses predictors for regression problems. The predictors are regression models of any type that can form centroidal Voronoi tessellations which are a function of their losses during training. It is proved that this structured model can efficiently interpolate this tessellation and approximate the multiple hypotheses target distribution and is equivalent to interpolating the meta-loss of the predictors, the loss being a zero set of the interpolation error. This model has a fixed-point iteration algorithm between the predictors and the centers of the basis functions. Diversity in learning can be controlled parametrically by truncating the tessellation formation with the losses of individual predictors. A closed-form solution with least-squares is presented, which to the authors knowledge, is the fastest solution in the literature for multiple hypotheses and structured predictions. Superior generalization performance and computational efficiency is achieved using only two-layer neural networks as predictors controlling diversity as a key component of success. A gradient-descent approach is introduced which is loss-agnostic regarding the predictors. The expected value for the loss of the structured model with Gaussian basis functions is computed, finding that correlation between predictors is not an appropriate tool for diversification. The experiments show outperformance with respect to the top competitors in the literature.

Continual learning-based probabilistic slow feature analysis for multimode dynamic process monitoring

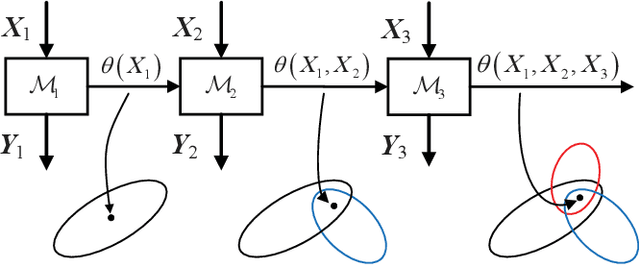
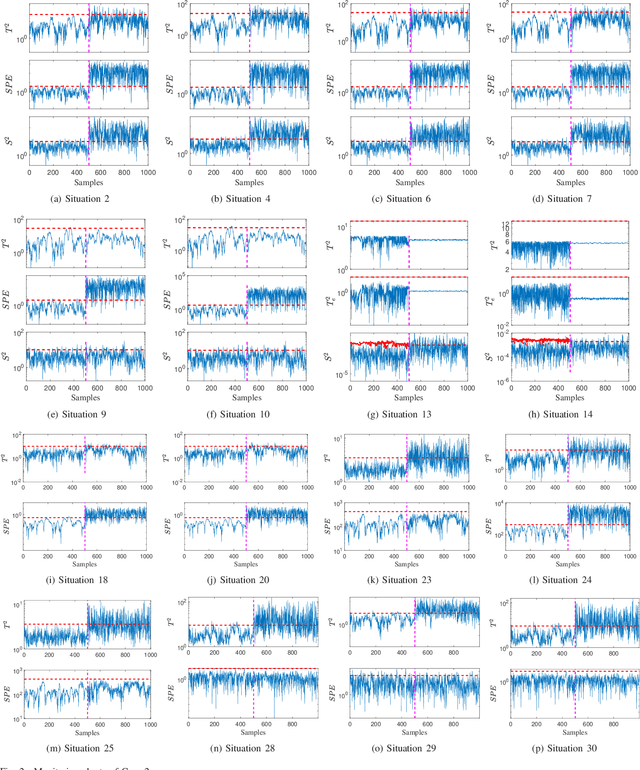
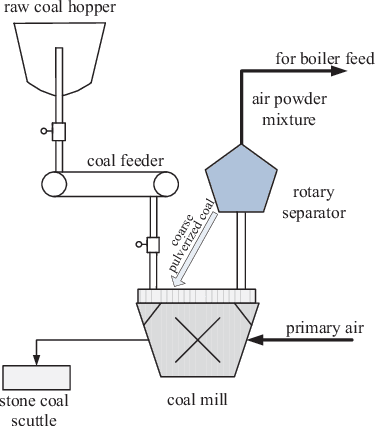
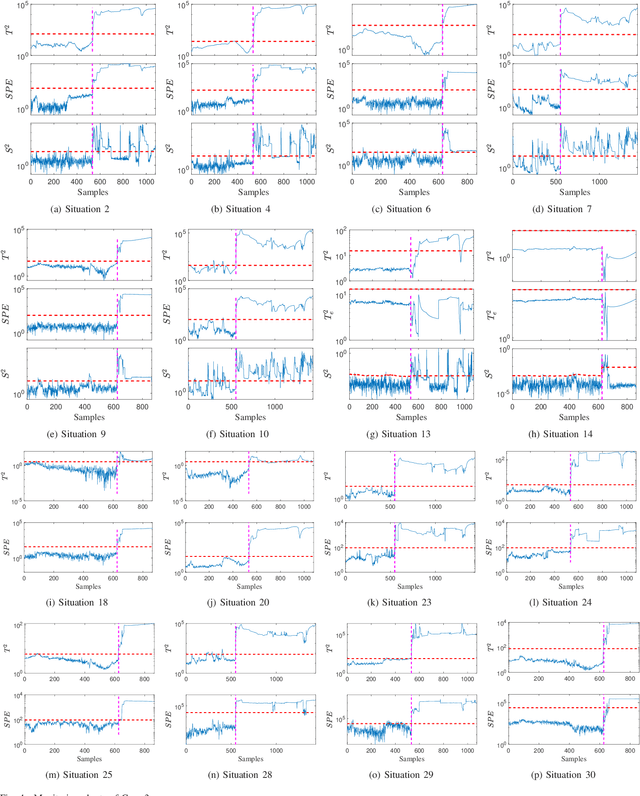
In this paper, a novel multimode dynamic process monitoring approach is proposed by extending elastic weight consolidation (EWC) to probabilistic slow feature analysis (PSFA) in order to extract multimode slow features for online monitoring. EWC was originally introduced in the setting of machine learning of sequential multi-tasks with the aim of avoiding catastrophic forgetting issue, which equally poses as a major challenge in multimode dynamic process monitoring. When a new mode arrives, a set of data should be collected so that this mode can be identified by PSFA and prior knowledge. Then, a regularization term is introduced to prevent new data from significantly interfering with the learned knowledge, where the parameter importance measures are estimated. The proposed method is denoted as PSFA-EWC, which is updated continually and capable of achieving excellent performance for successive modes. Different from traditional multimode monitoring algorithms, PSFA-EWC furnishes backward and forward transfer ability. The significant features of previous modes are retained while consolidating new information, which may contribute to learning new relevant modes. Compared with several known methods, the effectiveness of the proposed method is demonstrated via a continuous stirred tank heater and a practical coal pulverizing system.

Process monitoring based on orthogonal locality preserving projection with maximum likelihood estimation

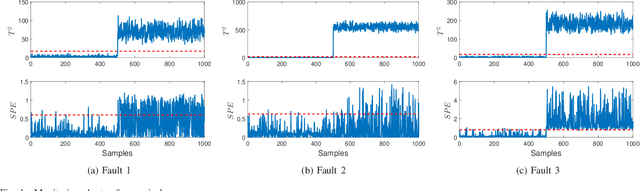
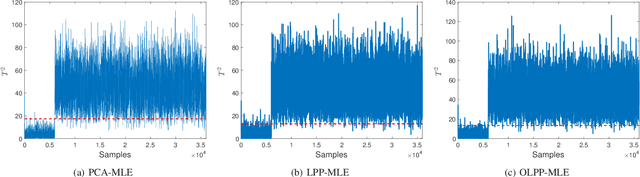
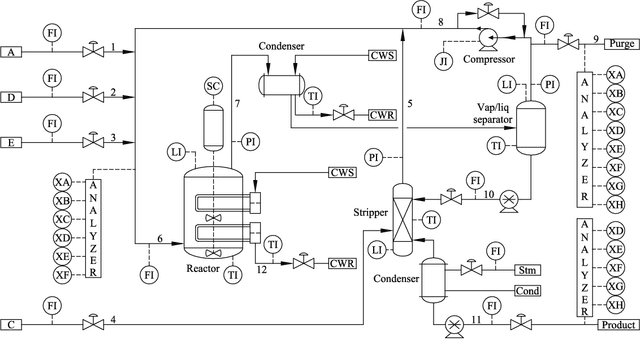
By integrating two powerful methods of density reduction and intrinsic dimensionality estimation, a new data-driven method, referred to as OLPP-MLE (orthogonal locality preserving projection-maximum likelihood estimation), is introduced for process monitoring. OLPP is utilized for dimensionality reduction, which provides better locality preserving power than locality preserving projection. Then, the MLE is adopted to estimate intrinsic dimensionality of OLPP. Within the proposed OLPP-MLE, two new static measures for fault detection $T_{\scriptscriptstyle {OLPP}}^2$ and ${\rm SPE}_{\scriptscriptstyle {OLPP}}$ are defined. In order to reduce algorithm complexity and ignore data distribution, kernel density estimation is employed to compute thresholds for fault diagnosis. The effectiveness of the proposed method is demonstrated by three case studies.

An improved mixture of probabilistic PCA for nonlinear data-driven process monitoring

An improved mixture of probabilistic principal component analysis (PPCA) has been introduced for nonlinear data-driven process monitoring in this paper. To realize this purpose, the technique of a mixture of probabilistic principal component analysers is utilized to establish the model of the underlying nonlinear process with local PPCA models, where a novel composite monitoring statistic is proposed based on the integration of two monitoring statistics in modified PPCA-based fault detection approach. Besides, the weighted mean of the monitoring statistics aforementioned is utilised as a metrics to detect potential abnormalities. The virtues of the proposed algorithm have been discussed in comparison with several unsupervised algorithms. Finally, Tennessee Eastman process and an autosuspension model are employed to demonstrate the effectiveness of the proposed scheme further.

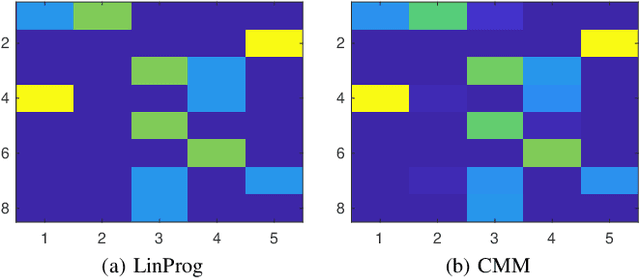
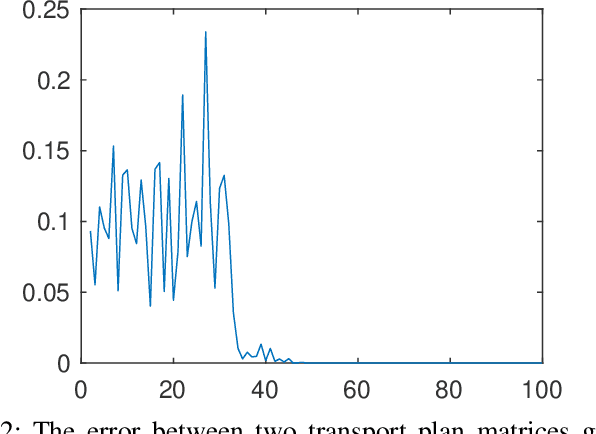
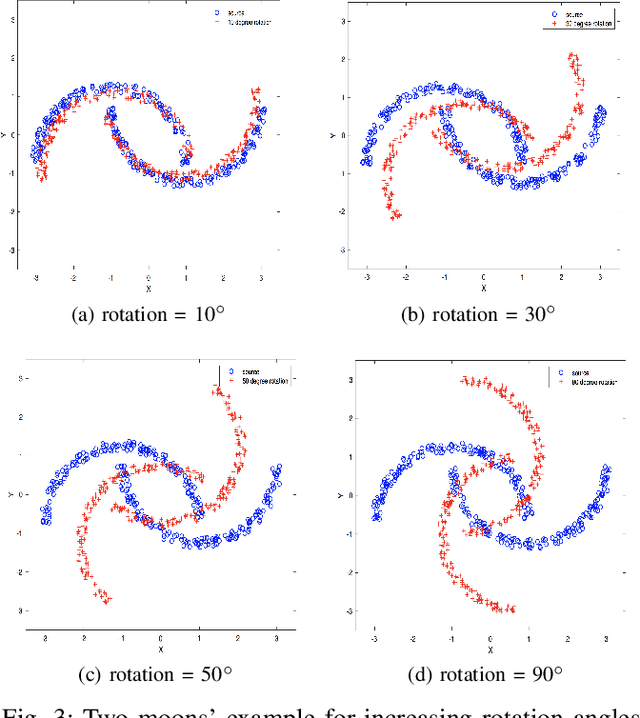
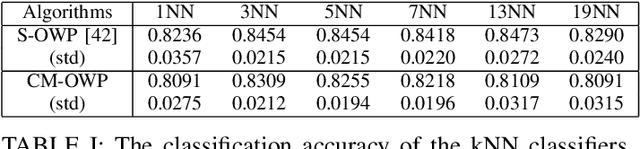
Coupling Matrix Manifolds and Their Applications in Optimal Transport

Optimal transport (OT) is a powerful tool for measuring the distance between two defined probability distributions. In this paper, we develop a new manifold named the coupling matrix manifold (CMM), where each point on CMM can be regarded as the transportation plan of the OT problem. We firstly explore the Riemannian geometry of CMM with the metric expressed by the Fisher information. These geometrical features of CMM have paved the way for developing numerical Riemannian optimization algorithms such as Riemannian gradient descent and Riemannian trust-region algorithms, forming a uniform optimization method for all types of OT problems. The proposed method is then applied to solve several OT problems studied by previous literature. The results of the numerical experiments illustrate that the optimization algorithms that are based on the method proposed in this paper are comparable to the classic ones, for example, the Sinkhorn algorithm, while outperforming other state-of-the-art algorithms without considering the geometry information, especially in the case of non-entropy optimal transport.

Sparse Least Squares Low Rank Kernel Machines

A general framework of least squares support vector machine with low rank kernels, referred to as LR-LSSVM, is introduced in this paper. The special structure of low rank kernels with a controlled model size brings sparsity as well as computational efficiency to the proposed model. Meanwhile, a two-step optimization algorithm with three different criteria is proposed and various experiments are carried out using the example of the so-call robust RBF kernel to validate the model. The experiment results show that the performance of the proposed algorithm is comparable or superior to several existing kernel machines.

l1-norm Penalized Orthogonal Forward Regression

A l1-norm penalized orthogonal forward regression (l1-POFR) algorithm is proposed based on the concept of leaveone- out mean square error (LOOMSE). Firstly, a new l1-norm penalized cost function is defined in the constructed orthogonal space, and each orthogonal basis is associated with an individually tunable regularization parameter. Secondly, due to orthogonal computation, the LOOMSE can be analytically computed without actually splitting the data set, and moreover a closed form of the optimal regularization parameter in terms of minimal LOOMSE is derived. Thirdly, a lower bound for regularization parameters is proposed, which can be used for robust LOOMSE estimation by adaptively detecting and removing regressors to an inactive set so that the computational cost of the algorithm is significantly reduced. Illustrative examples are included to demonstrate the effectiveness of this new l1-POFR approach.

Low Rank Representation on Riemannian Manifold of Square Root Densities

In this paper, we present a novel low rank representation (LRR) algorithm for data lying on the manifold of square root densities. Unlike traditional LRR methods which rely on the assumption that the data points are vectors in the Euclidean space, our new algorithm is designed to incorporate the intrinsic geometric structure and geodesic distance of the manifold. Experiments on several computer vision datasets showcase its noise robustness and superior performance on classification and subspace clustering compared to other state-of-the-art approaches.