Process monitoring based on orthogonal locality preserving projection with maximum likelihood estimation
Paper and Code
Dec 13, 2020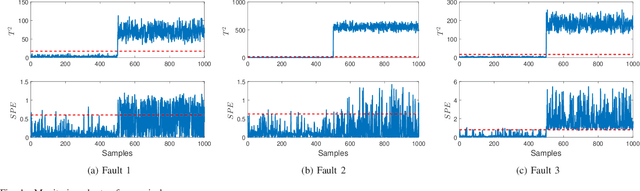
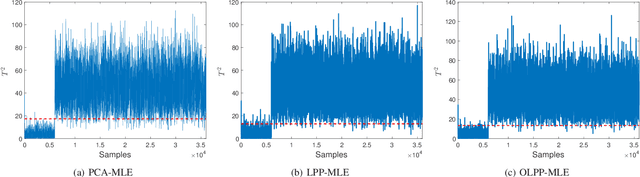

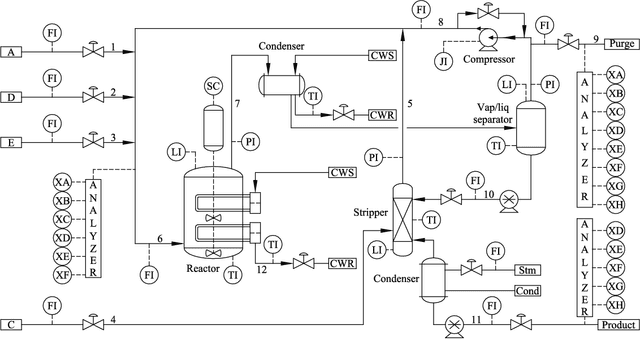
By integrating two powerful methods of density reduction and intrinsic dimensionality estimation, a new data-driven method, referred to as OLPP-MLE (orthogonal locality preserving projection-maximum likelihood estimation), is introduced for process monitoring. OLPP is utilized for dimensionality reduction, which provides better locality preserving power than locality preserving projection. Then, the MLE is adopted to estimate intrinsic dimensionality of OLPP. Within the proposed OLPP-MLE, two new static measures for fault detection $T_{\scriptscriptstyle {OLPP}}^2$ and ${\rm SPE}_{\scriptscriptstyle {OLPP}}$ are defined. In order to reduce algorithm complexity and ignore data distribution, kernel density estimation is employed to compute thresholds for fault diagnosis. The effectiveness of the proposed method is demonstrated by three case studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge