Simplifying Adversarially Robust PAC Learning with Tolerance

Adversarially robust PAC learning has proved to be challenging, with the currently best known learners [Montasser et al., 2021a] relying on improper methods based on intricate compression schemes, resulting in sample complexity exponential in the VC-dimension. A series of follow up work considered a slightly relaxed version of the problem called adversarially robust learning with tolerance [Ashtiani et al., 2023, Bhattacharjee et al., 2023, Raman et al., 2024] and achieved better sample complexity in terms of the VC-dimension. However, those algorithms were either improper and complex, or required additional assumptions on the hypothesis class H. We prove, for the first time, the existence of a simpler learner that achieves a sample complexity linear in the VC-dimension without requiring additional assumptions on H. Even though our learner is improper, it is "almost proper" in the sense that it outputs a hypothesis that is "similar" to a hypothesis in H. We also use the ideas from our algorithm to construct a semi-supervised learner in the tolerant setting. This simple algorithm achieves comparable bounds to the previous (non-tolerant) semi-supervised algorithm of Attias et al. [2022a], but avoids the use of intricate subroutines from previous works, and is "almost proper."

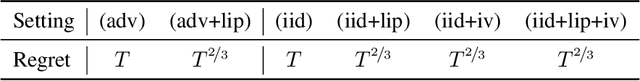
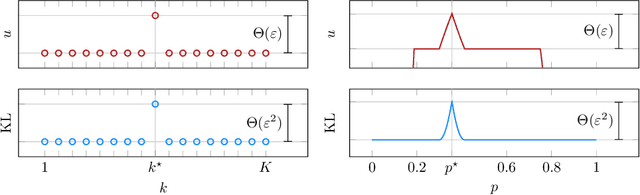
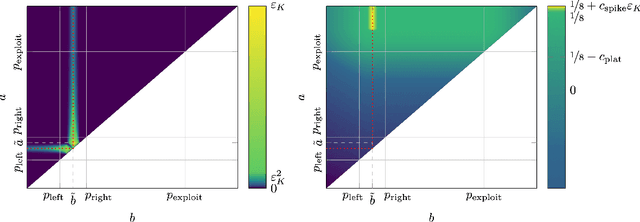
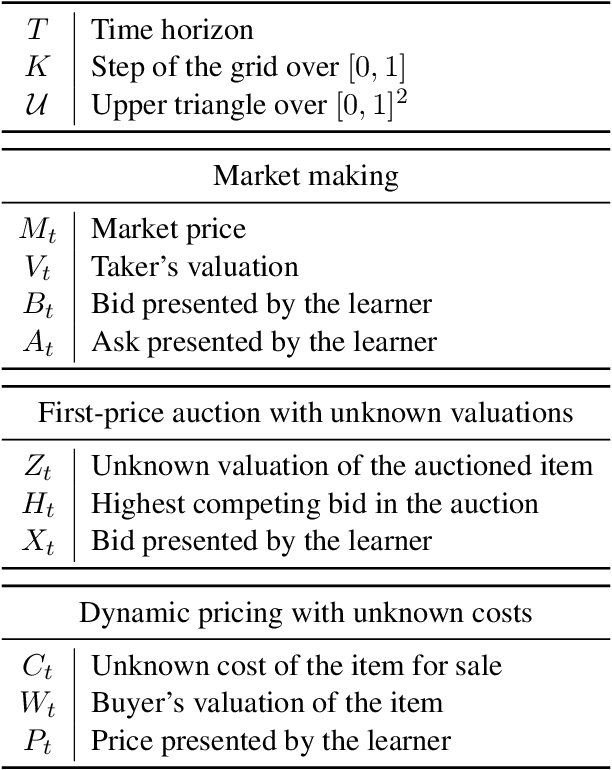
Market Making without Regret

We consider a sequential decision-making setting where, at every round $t$, a market maker posts a bid price $B_t$ and an ask price $A_t$ to an incoming trader (the taker) with a private valuation for one unit of some asset. If the trader's valuation is lower than the bid price, or higher than the ask price, then a trade (sell or buy) occurs. If a trade happens at round $t$, then letting $M_t$ be the market price (observed only at the end of round $t$), the maker's utility is $M_t - B_t$ if the maker bought the asset, and $A_t - M_t$ if they sold it. We characterize the maker's regret with respect to the best fixed choice of bid and ask pairs under a variety of assumptions (adversarial, i.i.d., and their variants) on the sequence of market prices and valuations. Our upper bound analysis unveils an intriguing connection relating market making to first-price auctions and dynamic pricing. Our main technical contribution is a lower bound for the i.i.d. case with Lipschitz distributions and independence between prices and valuations. The difficulty in the analysis stems from the unique structure of the reward and feedback functions, allowing an algorithm to acquire information by graduating the "cost of exploration" in an arbitrary way.

Multi-scale gigapixel microscopy using a multi-camera array microscope

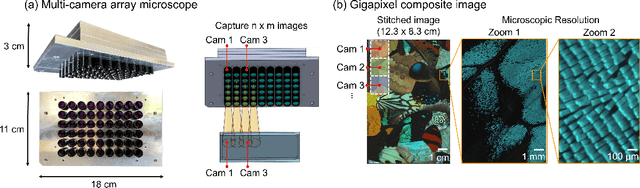
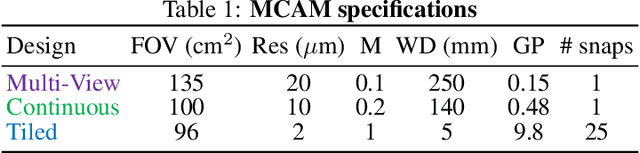
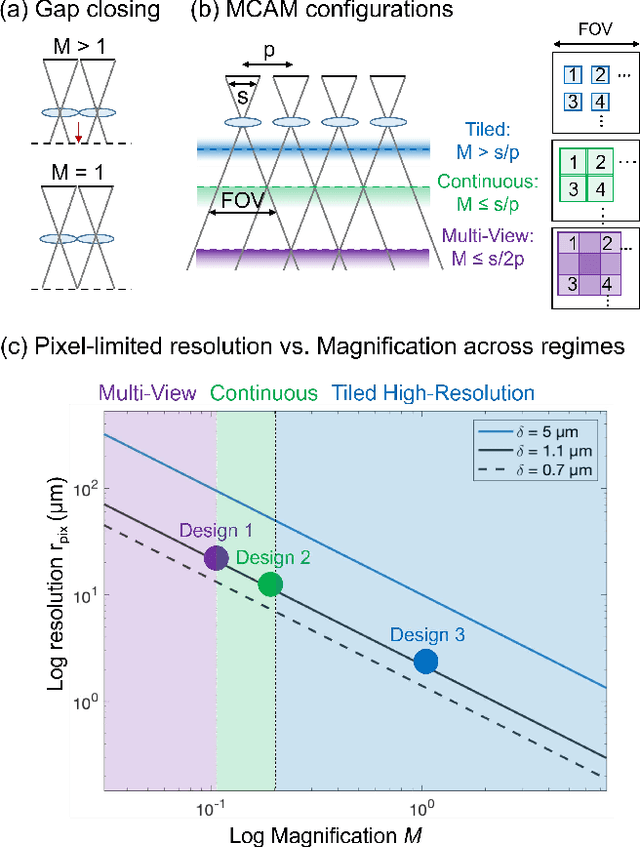
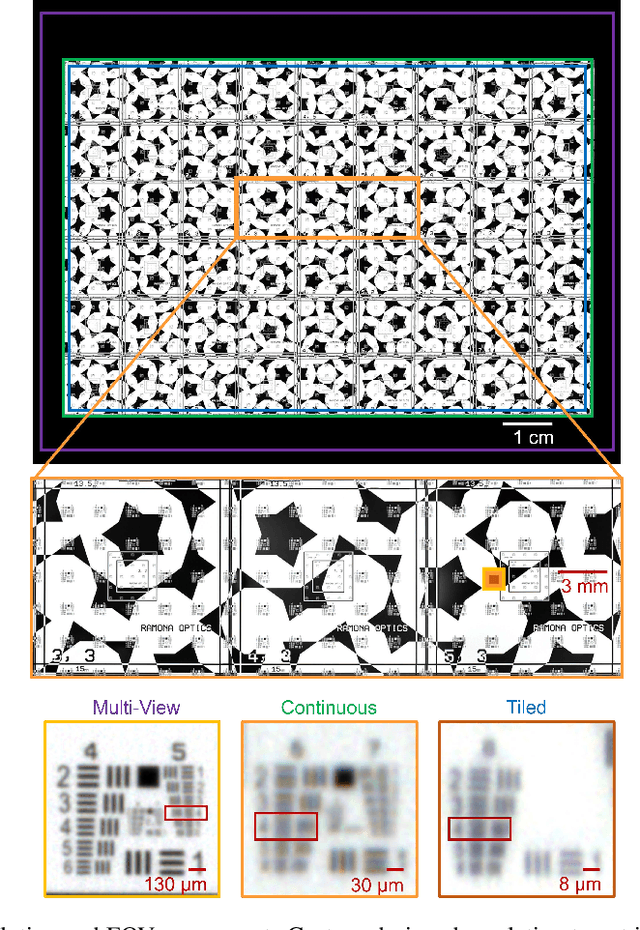
This article experimentally examines different configurations of a novel multi-camera array microscope (MCAM) imaging technology. The MCAM is based upon a densely packed array of "micro-cameras" to jointly image across a large field-of-view at high resolution. Each micro-camera within the array images a unique area of a sample of interest, and then all acquired data with 54 micro-cameras are digitally combined into composite frames, whose total pixel counts significantly exceed the pixel counts of standard microscope systems. We present results from three unique MCAM configurations for different use cases. First, we demonstrate a configuration that simultaneously images and estimates the 3D object depth across a 100 x 135 mm^2 field-of-view (FOV) at approximately 20 um resolution, which results in 0.15 gigapixels (GP) per snapshot. Second, we demonstrate an MCAM configuration that records video across a continuous 83 x 123 mm^2 FOV with two-fold increased resolution (0.48 GP per frame). Finally, we report a third high-resolution configuration (2 um resolution) that can rapidly produce 9.8 GP composites of large histopathology specimens.

Tensorial tomographic differential phase-contrast microscopy

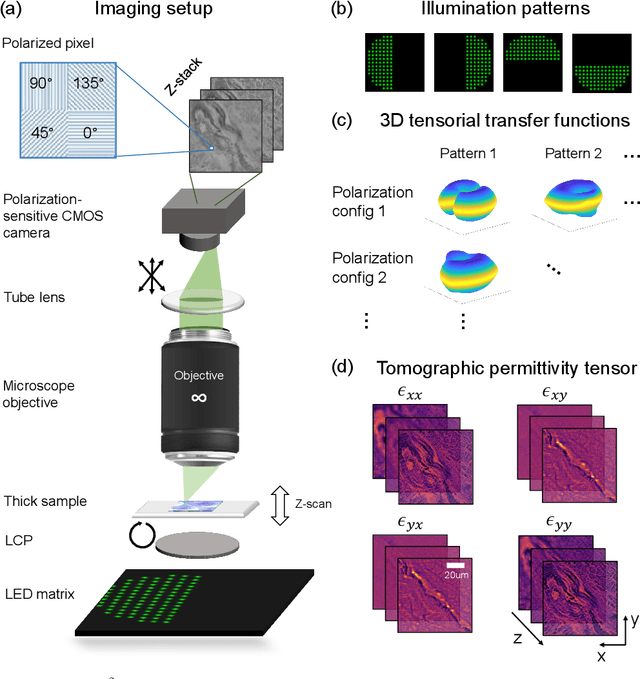
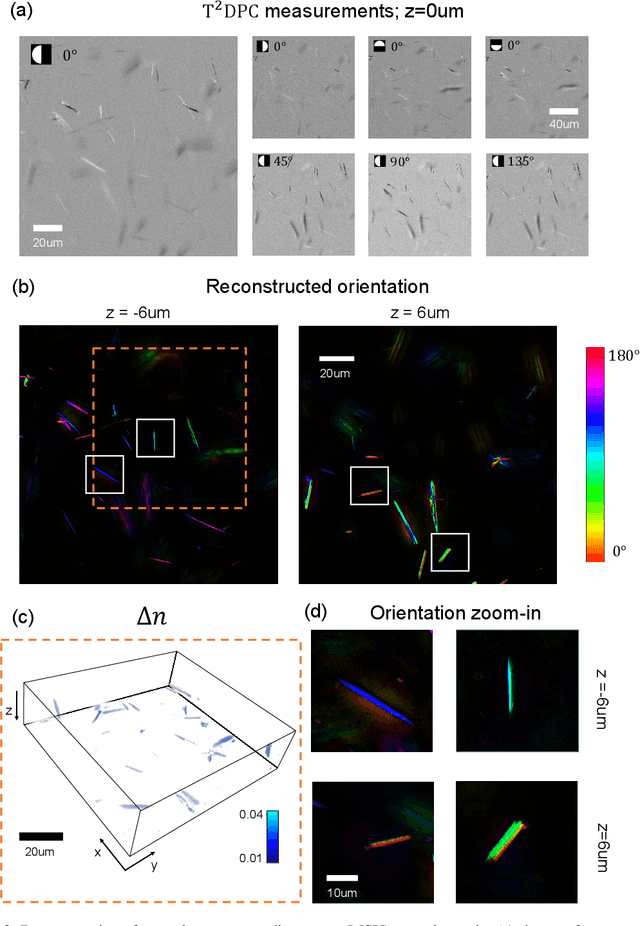
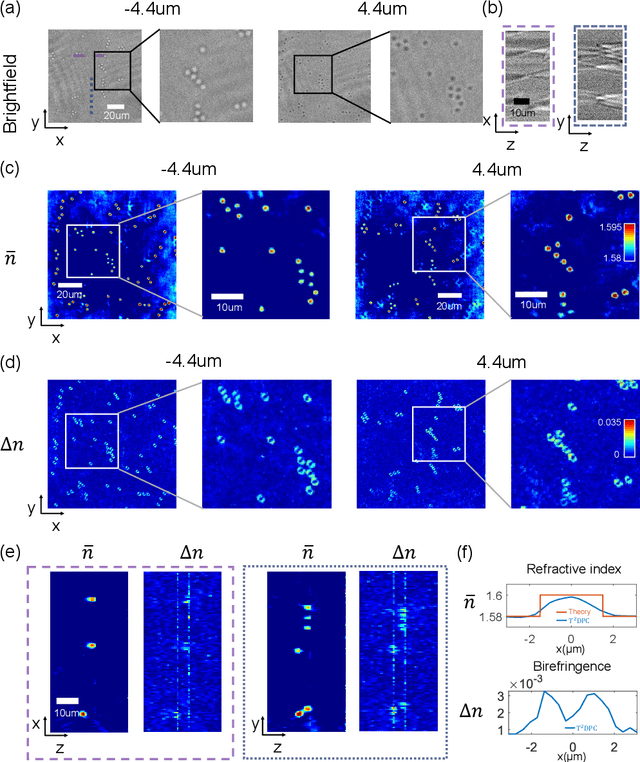
We report Tensorial Tomographic Differential Phase-Contrast microscopy (T2DPC), a quantitative label-free tomographic imaging method for simultaneous measurement of phase and anisotropy. T2DPC extends differential phase-contrast microscopy, a quantitative phase imaging technique, to highlight the vectorial nature of light. The method solves for permittivity tensor of anisotropic samples from intensity measurements acquired with a standard microscope equipped with an LED matrix, a circular polarizer, and a polarization-sensitive camera. We demonstrate accurate volumetric reconstructions of refractive index, birefringence, and orientation for various validation samples, and show that the reconstructed polarization structures of a biological specimen are predictive of pathology.

Adversarially Robust Learning with Tolerance

We study the problem of tolerant adversarial PAC learning with respect to metric perturbation sets. In adversarial PAC learning, an adversary is allowed to replace a test point $x$ with an arbitrary point in a closed ball of radius $r$ centered at $x$. In the tolerant version, the error of the learner is compared with the best achievable error with respect to a slightly larger perturbation radius $(1+\gamma)r$. For perturbation sets with doubling dimension $d$, we show that a variant of the natural ``perturb-and-smooth'' algorithm PAC learns any hypothesis class $\mathcal{H}$ with VC dimension $v$ in the $\gamma$-tolerant adversarial setting with $O\left(\frac{v(1+1/\gamma)^{O(d)}}{\varepsilon}\right)$ samples. This is the first such general guarantee with linear dependence on $v$ even for the special case where the domain is the real line and the perturbation sets are closed balls (intervals) of radius $r$. However, the proposed guarantees for the perturb-and-smooth algorithm currently only hold in the tolerant robust realizable setting and exhibit exponential dependence on $d$. We additionally propose an alternative learning method which yields sample complexity bounds with only linear dependence on the doubling dimension even in the more general agnostic case. This approach is based on sample compression.

Increasing a microscope's effective field of view via overlapped imaging and machine learning

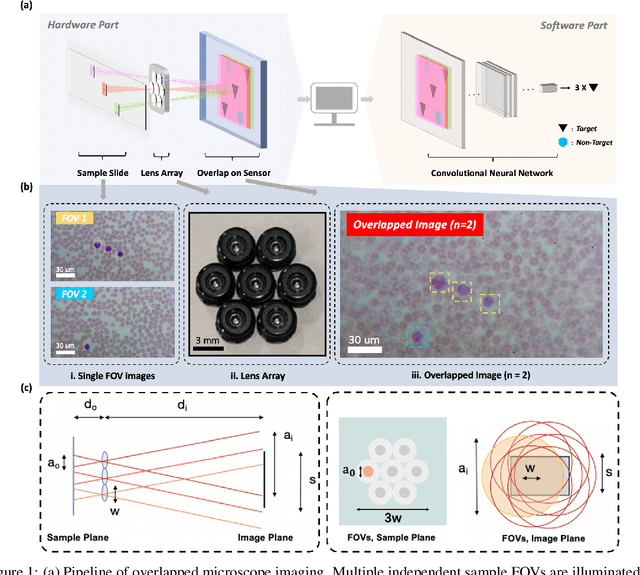
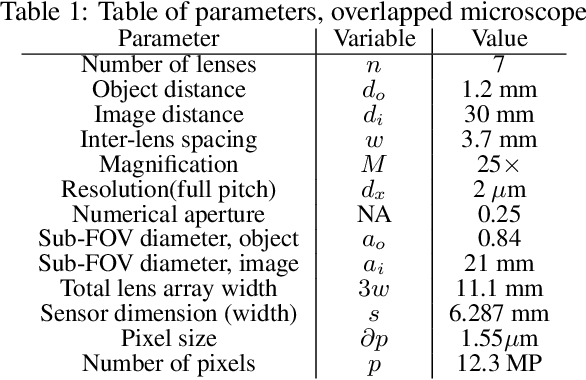
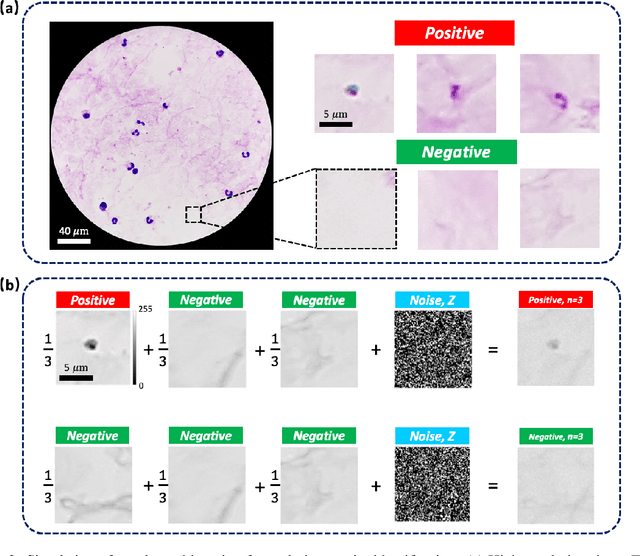
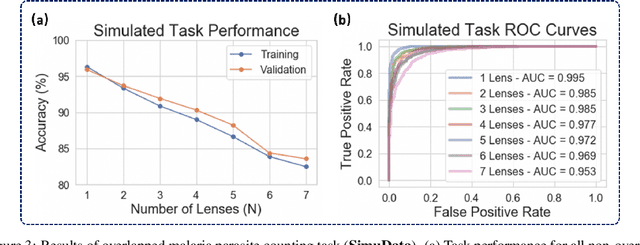
This work demonstrates a multi-lens microscopic imaging system that overlaps multiple independent fields of view on a single sensor for high-efficiency automated specimen analysis. Automatic detection, classification and counting of various morphological features of interest is now a crucial component of both biomedical research and disease diagnosis. While convolutional neural networks (CNNs) have dramatically improved the accuracy of counting cells and sub-cellular features from acquired digital image data, the overall throughput is still typically hindered by the limited space-bandwidth product (SBP) of conventional microscopes. Here, we show both in simulation and experiment that overlapped imaging and co-designed analysis software can achieve accurate detection of diagnostically-relevant features for several applications, including counting of white blood cells and the malaria parasite, leading to multi-fold increase in detection and processing throughput with minimal reduction in accuracy.

Black-box Certification and Learning under Adversarial Perturbations

We formally study the problem of classification under adversarial perturbations, both from the learner's perspective, and from the viewpoint of a third-party who aims at certifying the robustness of a given black-box classifier. We analyze a PAC-type framework of semi-supervised learning and identify possibility and impossibility results for proper learning of VC-classes in this setting. We further introduce and study a new setting of black-box certification under limited query budget. We analyze this for various classes of predictors and types of perturbation. We also consider the viewpoint of a black-box adversary that aims at finding adversarial examples, showing that the existence of an adversary with polynomial query complexity implies the existence of a robust learner with small sample complexity.