Market Making without Regret
Paper and Code
Nov 21, 2024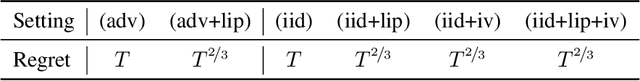
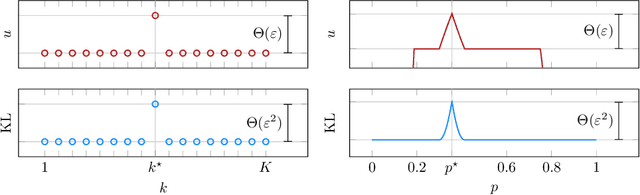
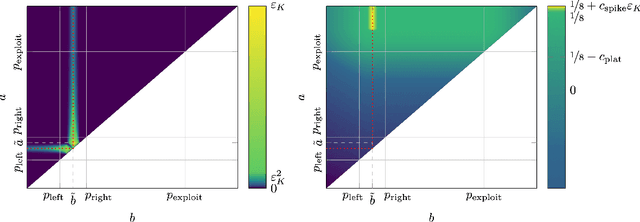
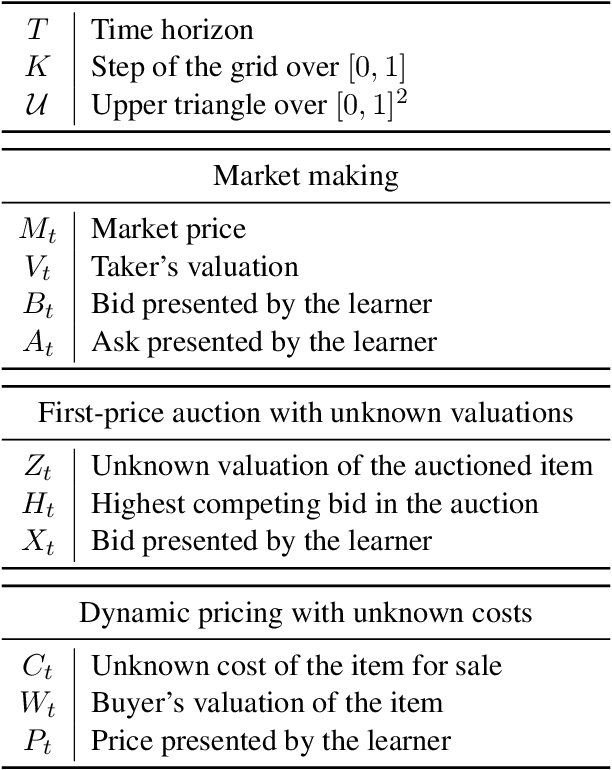
We consider a sequential decision-making setting where, at every round $t$, a market maker posts a bid price $B_t$ and an ask price $A_t$ to an incoming trader (the taker) with a private valuation for one unit of some asset. If the trader's valuation is lower than the bid price, or higher than the ask price, then a trade (sell or buy) occurs. If a trade happens at round $t$, then letting $M_t$ be the market price (observed only at the end of round $t$), the maker's utility is $M_t - B_t$ if the maker bought the asset, and $A_t - M_t$ if they sold it. We characterize the maker's regret with respect to the best fixed choice of bid and ask pairs under a variety of assumptions (adversarial, i.i.d., and their variants) on the sequence of market prices and valuations. Our upper bound analysis unveils an intriguing connection relating market making to first-price auctions and dynamic pricing. Our main technical contribution is a lower bound for the i.i.d. case with Lipschitz distributions and independence between prices and valuations. The difficulty in the analysis stems from the unique structure of the reward and feedback functions, allowing an algorithm to acquire information by graduating the "cost of exploration" in an arbitrary way.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge