Estimating Infinite-Dimensional Continuum Robot States From the Tip

Knowing the state of a robot is critical for many problems, such as feedback control. For continuum robots, state estimation is incredibly challenging. First, the motion of a continuum robot involves many kinematic states, including poses, strains, and velocities. Second, all these states are infinite-dimensional due to the robot's flexible property. It has remained unclear whether these infinite-dimensional states are observable at all using existing sensing techniques. Recently, we presented a solution to this challenge. It was a mechanics-based dynamic state estimation algorithm, called a Cosserat theoretic boundary observer, which could recover all the infinite-dimensional robot states by only measuring the velocity twist of the tip. In this work, we generalize the algorithm to incorporate tip pose measurements for more tuning freedom. We also validate this algorithm offline using recorded experimental data of a tendon-driven continuum robot. Specifically, we feed the recorded tension of the tendon and the recorded tip measurements into a numerical solver of the Cosserat rod model based on our continuum robot. It is observed that, even with purposely deviated initialization, the state estimates by our algorithm quickly converge to the recorded ground truth states and closely follow the robot's actual motion.

Learning Evacuee Models from Robot-Guided Emergency Evacuation Experiments

Recent research has examined the possibility of using robots to guide evacuees to safe exits during emergencies. Yet, there are many factors that can impact a person's decision to follow a robot. Being able to model how an evacuee follows an emergency robot guide could be crucial for designing robots that effectively guide evacuees during an emergency. This paper presents a method for developing realistic and predictive human evacuee models from physical human evacuation experiments. The paper analyzes the behavior of 14 human subjects during physical robot-guided evacuation. We then use the video data to create evacuee motion models that predict the person's future positions during the emergency. Finally, we validate the resulting models by running a k-fold cross-validation on the data collected during physical human subject experiments. We also present performance results of the model using data from a similar simulated emergency evacuation experiment demonstrating that these models can serve as a tool to predict evacuee behavior in novel evacuation simulations.

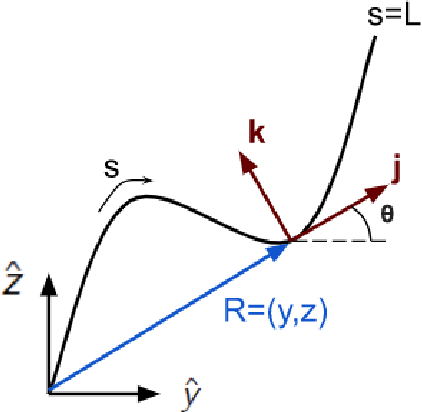
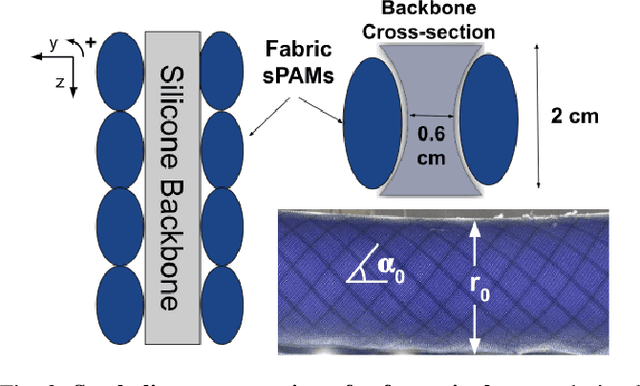
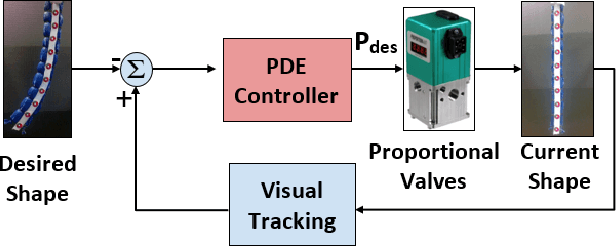
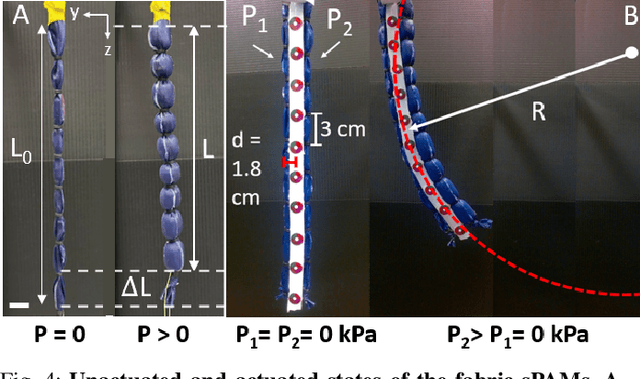
Stable Real-Time Feedback Control of a Pneumatic Soft Robot

Soft actuators offer compliant and safe interaction with an unstructured environment compared to their rigid counterparts. However, control of these systems is often challenging because they are inherently under-actuated, have infinite degrees of freedom (DoF), and their mechanical properties can change by unknown external loads. Existing works mainly relied on discretization and reduction, suffering from either low accuracy or high computational cost for real-time control purposes. Recently, we presented an infinite-dimensional feedback controller for soft manipulators modeled by partial differential equations (PDEs) based on the Cosserat rod theory. In this study, we examine how to implement this controller in real-time using only a limited number of actuators. To do so, we formulate a convex quadratic programming problem that tunes the feedback gains of the controller in real time such that it becomes realizable by the actuators. We evaluated the controller's performance through experiments on a physical soft robot capable of planar motions and show that the actual controller implemented by the finite-dimensional actuators still preserves the stabilizing property of the desired infinite-dimensional controller. This research fills the gap between the infinite-dimensional control design and finite-dimensional actuation in practice and suggests a promising direction for exploring PDE-based control design for soft robots.

Full State Estimation of Soft Robots From Tip Velocities: A Cosserat-Theoretic Boundary Observer

Soft robotics is a rapidly growing research area in robotics. Sensing of robotic systems is important for designing feedback controllers which usually provide robustness to modeling uncertainties. Sensing of soft robots, however, is considered a challenging task because theoretically, soft robots have infinite degrees of freedom while existing sensors only provide a limited number of measurements. One solution to this challenge is to design an observer/filter to estimate the unknown states from the sensor measurements. In this work, we design a boundary observer for soft robots based on the well-known Cosserat rod theory which models soft robots by nonlinear partial differential equations (PDEs). This boundary observer is able to estimate all the continuous robot states (poses, strains, and velocities) using the PDE model, inputs, and only tip velocity measurements (which explains the name "boundary" observer). The key idea is to inject sequential tip velocity measurements into the observer in a way that dissipates the energy of state estimation errors through the boundary. This boundary observer only requires sensing the tip velocity, can be implemented by simply changing a boundary condition in any numerical solvers of Cosserat rod models, and is proven to be locally input-to-state stable. Simulation studies are included and suggest that the domain of attraction is large and the observer is robust to measurement noise.

Multi-Robot-Guided Crowd Evacuation: Two-Scale Modeling and Control Based on Mean-Field Hydrodynamic Models

Emergency evacuation describes a complex situation involving time-critical decision-making by evacuees. Mobile robots are being actively explored as a potential solution to provide timely guidance. In this work, we study a robot-guided crowd evacuation problem where a small group of robots is used to guide a large human crowd to safe locations. The challenge lies in how to utilize micro-level human-robot interactions to indirectly influence a population that significantly outnumbers the robots to achieve the collective evacuation objective. To address the challenge, we follow a two-scale modeling strategy and explore mean-field hydrodynamic models which consist of a family of microscopic social-force models that explicitly describe how human movements are locally affected by other humans, the environment, and the robots, and associated macroscopic equations for the temporal and spatial evolution of the crowd density and flow velocity. We design controllers for the robots such that they not only automatically explore the environment (with unknown dynamic obstacles) to cover it as much as possible but also dynamically adjust the directions of their local navigation force fields based on the real-time macro-states of the crowd to guide the crowd to a safe location. We prove the stability of the proposed evacuation algorithm and conduct a series of simulations (involving unknown dynamic obstacles) to validate the performance of the algorithm.

Task Space Tracking of Soft Manipulators: Inner-Outer Loop Control Based on Cosserat-Rod Models

Soft robots are robotic systems made of deformable materials and exhibit unique flexibility that can be exploited for complex environments and tasks. However, their control problem has been considered a challenging subject because they are of infinite degrees of freedom and highly under-actuated. Existing studies have mainly relied on simplified and approximated finite-dimensional models. In this work, we exploit infinite-dimensional nonlinear control for soft robots. We adopt the Cosserat-rod theory and employ nonlinear partial differential equations (PDEs) to model the kinematics and dynamics of soft manipulators, including their translational motions (for shear and elongation) and rotational motions (for bending and torsion). The objective is to achieve position tracking of the whole manipulator in a planar task space by controlling the moments (generated by actuators). The control design is inspired by the energy decay property of damped wave equations and has an inner-outer loop structure. In the outer loop, we design desired rotational motions that rotate the translational component into a direction that asymptotically dissipates the energy associated with position tracking errors. In the inner loop, we design inputs for the rotational components to track their desired motions, again by dissipating the rotational energy. We prove that the closed-loop system is exponentially stable and evaluate its performance through simulations.

Multi-Robot-Assisted Human Crowd Evacuation using Navigation Velocity Fields

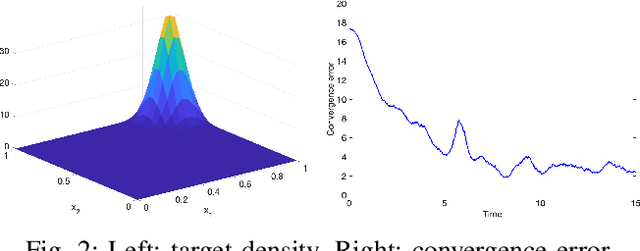
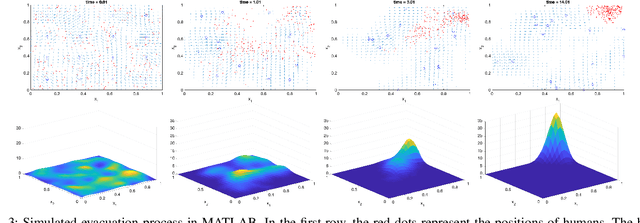
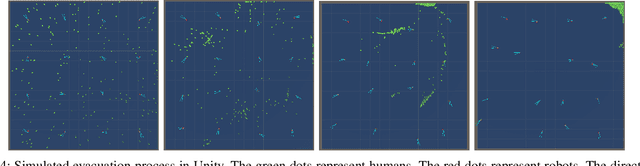
This work studies a robot-assisted crowd evacuation problem where we control a small group of robots to guide a large human crowd to safe locations. The challenge lies in how to model human-robot interactions and design robot controls to indirectly control a human population that significantly outnumbers the robots. To address the challenge, we treat the crowd as a continuum and formulate the evacuation objective as driving the crowd density to target locations. We propose a novel mean-field model which consists of a family of microscopic equations that explicitly model how human motions are locally guided by the robots and an associated macroscopic equation that describes how the crowd density is controlled by the navigation velocity fields generated by all robots. Then, we design density feedback controllers for the robots to dynamically adjust their states such that the generated navigation velocity fields drive the crowd density to a target density. Stability guarantees of the proposed controllers are proven. Agent-based simulations are included to evaluate the proposed evacuation algorithms.

PDE-based Dynamic Control and Estimation of Soft Robotic Arms

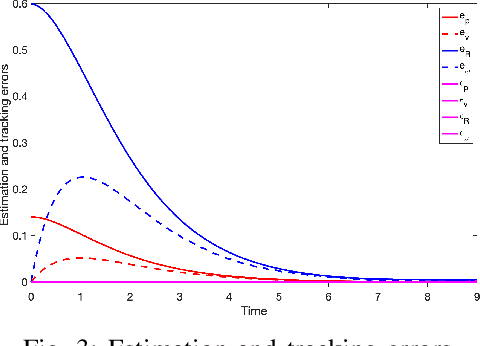
Compared with traditional rigid-body robots, soft robots not only exhibit unprecedented adaptation and flexibility, but also present novel challenges in their modelling and control because of their infinite degrees of freedom. Most of the existing approaches have mainly relied on approximated models so that the well-developed finite-dimensional control theory can be exploited. However, this Approximate-then-Design approach may bring in modelling uncertainty and performance degradation. Hence, we adopt the opposite approach and exploit infinite-dimensional analysis for soft robotic systems. Our control design is based on the increasingly adopted Cosserat rod model, which describes the kinematics and dynamics of soft robotic arms with a set of nonlinear partial differential equations (PDE). We design infinite-dimensional state feedback control laws for the Cosserat PDE model to achieve trajectory tracking in the task space (consisting of position, rotation, linear and angular velocities), and prove their uniform tracking convergence. To estimate the feedback states, we design an infinite-dimensional extended Kalman filter on Lie groups for the PDE system to estimate all the state variables (including position, rotation, strains, curvature, linear and angular velocities) using only position measurements. The proposed algorithms are evaluated using simulations.