A variational approach to geometric mechanics for undulating robotic locomotion

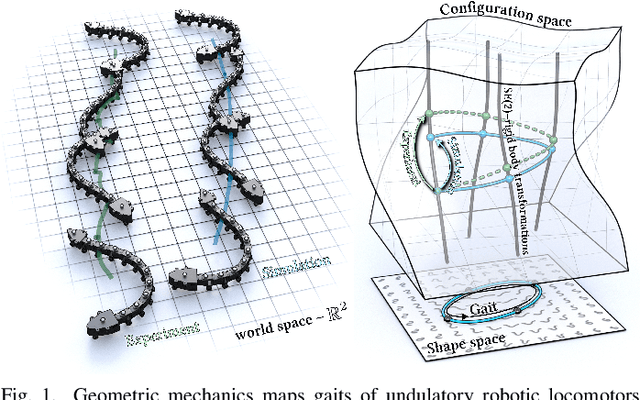
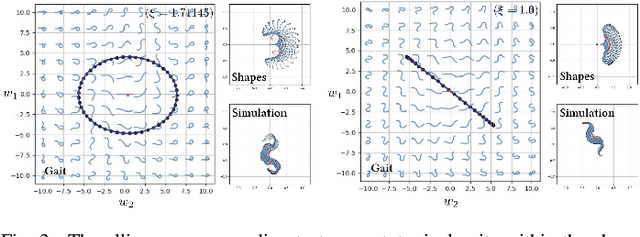
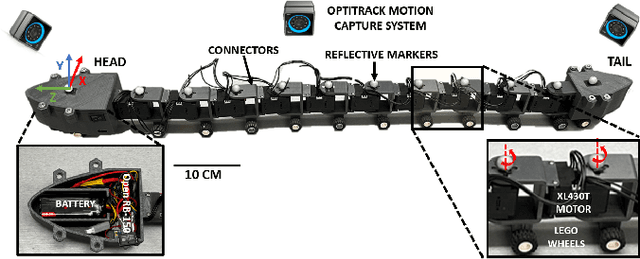
Limbless organisms of all sizes use undulating patterns of self-deformation to locomote. Geometric mechanics, which maps deformations to motions, provides a powerful framework to formalize and investigate the theoretical properties and limitations of such modes of locomotion. However, the inherent level of abstraction poses a challenge when bridging the gap between theory or simulations and laboratory experiments. We investigate the challenges of modeling motion trajectories of an undulating robotic locomotor by comparing experiments and simulations performed with a variational integrator. Despite the extensive simplifications that the model based on a geometric variation principle entails, the simulations show good agreement on average. Notably, our approach merely requires the knowledge of the \emph{dissipation metric} -- a Riemannian metric on the configuration space, which can in practice be approximated by means closely resembling \emph{resistive force theory}.

Machine Learning-Driven Burrowing with a Snake-Like Robot

Subterranean burrowing is inherently difficult for robots because of the high forces experienced as well as the high amount of uncertainty in this domain. Because of the difficulty in modeling forces in granular media, we propose the use of a novel machine-learning control strategy to obtain optimal techniques for vertical self-burrowing. In this paper, we realize a snake-like bio-inspired robot that is equipped with an IMU and two triple-axis magnetometers. Utilizing magnetic field strength as an analog for depth, a novel deep learning architecture was proposed based on sinusoidal and random data in order to obtain a more efficient strategy for vertical self-burrowing. This strategy was able to outperform many other standard burrowing techniques and was able to automatically reach targeted burrowing depths. We hope these results will serve as a proof of concept for how optimization can be used to unlock the secrets of navigating in the subterranean world more efficiently.

Locomotion and Obstacle Avoidance of a Worm-like Soft Robot

This paper presents a soft earthworm robot that is capable of both efficient locomotion and obstacle avoidance. The robot is designed to replicate the unique locomotion mechanisms of earthworms, which enable them to move through narrow and complex environments with ease. The robot consists of multiple segments, each with its own set of actuators, that are connected through rigid plastic joints, allowing for increased adaptability and flexibility in navigating different environments. The robot utilizes proprioceptive sensing and control algorithms to detect and avoid obstacles in real-time while maintaining efficient locomotion. The robot uses a pneumatic actuation system to mimic the circumnutation behavior exhibited by plant roots in order to navigate through complex environments. The results demonstrate the capabilities of the robot for navigating through cluttered environments, making this development significant for various fields of robotics, including search and rescue, environmental monitoring, and medical procedures.

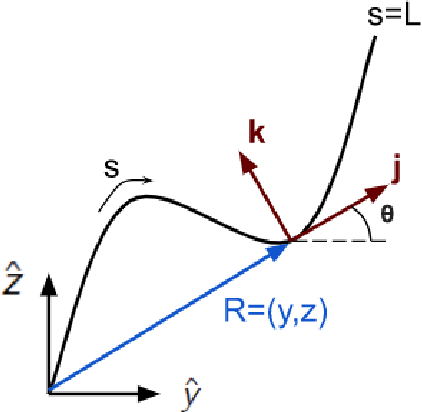
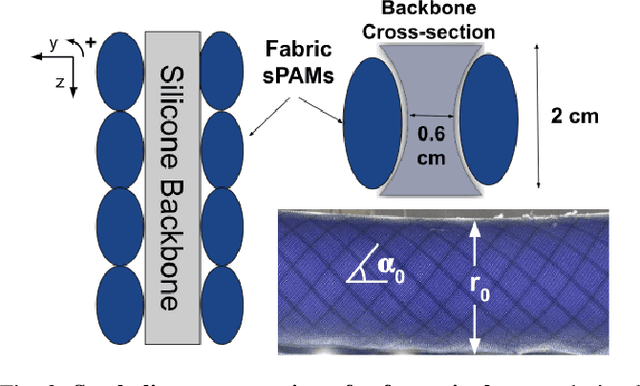
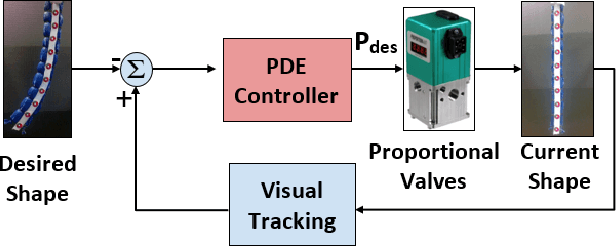
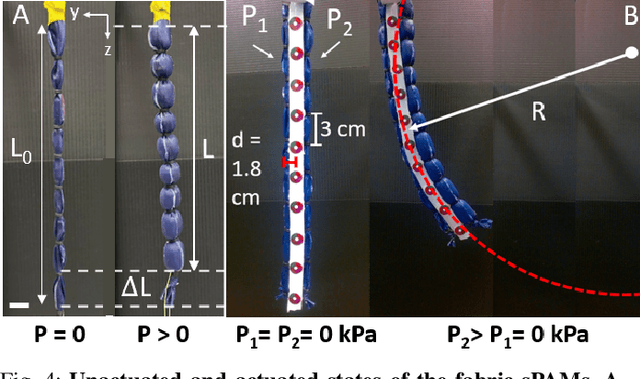
Stable Real-Time Feedback Control of a Pneumatic Soft Robot

Soft actuators offer compliant and safe interaction with an unstructured environment compared to their rigid counterparts. However, control of these systems is often challenging because they are inherently under-actuated, have infinite degrees of freedom (DoF), and their mechanical properties can change by unknown external loads. Existing works mainly relied on discretization and reduction, suffering from either low accuracy or high computational cost for real-time control purposes. Recently, we presented an infinite-dimensional feedback controller for soft manipulators modeled by partial differential equations (PDEs) based on the Cosserat rod theory. In this study, we examine how to implement this controller in real-time using only a limited number of actuators. To do so, we formulate a convex quadratic programming problem that tunes the feedback gains of the controller in real time such that it becomes realizable by the actuators. We evaluated the controller's performance through experiments on a physical soft robot capable of planar motions and show that the actual controller implemented by the finite-dimensional actuators still preserves the stabilizing property of the desired infinite-dimensional controller. This research fills the gap between the infinite-dimensional control design and finite-dimensional actuation in practice and suggests a promising direction for exploring PDE-based control design for soft robots.