PDE-based Dynamic Control and Estimation of Soft Robotic Arms

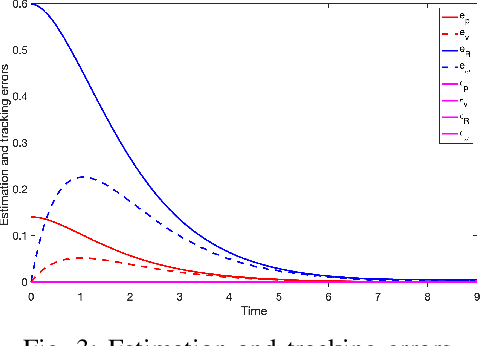
Compared with traditional rigid-body robots, soft robots not only exhibit unprecedented adaptation and flexibility, but also present novel challenges in their modelling and control because of their infinite degrees of freedom. Most of the existing approaches have mainly relied on approximated models so that the well-developed finite-dimensional control theory can be exploited. However, this Approximate-then-Design approach may bring in modelling uncertainty and performance degradation. Hence, we adopt the opposite approach and exploit infinite-dimensional analysis for soft robotic systems. Our control design is based on the increasingly adopted Cosserat rod model, which describes the kinematics and dynamics of soft robotic arms with a set of nonlinear partial differential equations (PDE). We design infinite-dimensional state feedback control laws for the Cosserat PDE model to achieve trajectory tracking in the task space (consisting of position, rotation, linear and angular velocities), and prove their uniform tracking convergence. To estimate the feedback states, we design an infinite-dimensional extended Kalman filter on Lie groups for the PDE system to estimate all the state variables (including position, rotation, strains, curvature, linear and angular velocities) using only position measurements. The proposed algorithms are evaluated using simulations.