Identifying Causal Direction via Variational Bayesian Compression

Telling apart the cause and effect between two random variables with purely observational data is a challenging problem that finds applications in various scientific disciplines. A key principle utilized in this task is the algorithmic Markov condition, which postulates that the joint distribution, when factorized according to the causal direction, yields a more succinct codelength compared to the anti-causal direction. Previous approaches approximate these codelengths by relying on simple functions or Gaussian processes (GPs) with easily evaluable complexity, compromising between model fitness and computational complexity. To overcome these limitations, we propose leveraging the variational Bayesian learning of neural networks as an interpretation of the codelengths. Consequently, we can enhance the model fitness while promoting the succinctness of the codelengths, while avoiding the significant computational complexity of the GP-based approaches. Extensive experiments on both synthetic and real-world benchmarks in cause-effect identification demonstrate the effectiveness of our proposed method, surpassing the overall performance of related complexity-based and structural causal model regression-based approaches.

Clustering-based Meta Bayesian Optimization with Theoretical Guarantee

Bayesian Optimization (BO) is a well-established method for addressing black-box optimization problems. In many real-world scenarios, optimization often involves multiple functions, emphasizing the importance of leveraging data and learned functions from prior tasks to enhance efficiency in the current task. To expedite convergence to the global optimum, recent studies have introduced meta-learning strategies, collectively referred to as meta-BO, to incorporate knowledge from historical tasks. However, in practical settings, the underlying functions are often heterogeneous, which can adversely affect optimization performance for the current task. Additionally, when the number of historical tasks is large, meta-BO methods face significant scalability challenges. In this work, we propose a scalable and robust meta-BO method designed to address key challenges in heterogeneous and large-scale meta-tasks. Our approach (1) effectively partitions transferred meta-functions into highly homogeneous clusters, (2) learns the geometry-based surrogate prototype that capture the structural patterns within each cluster, and (3) adaptively synthesizes meta-priors during the online phase using statistical distance-based weighting policies. Experimental results on real-world hyperparameter optimization (HPO) tasks, combined with theoretical guarantees, demonstrate the robustness and effectiveness of our method in overcoming these challenges.

h-Edit: Effective and Flexible Diffusion-Based Editing via Doob's h-Transform

We introduce a theoretical framework for diffusion-based image editing by formulating it as a reverse-time bridge modeling problem. This approach modifies the backward process of a pretrained diffusion model to construct a bridge that converges to an implicit distribution associated with the editing target at time 0. Building on this framework, we propose h-Edit, a novel editing method that utilizes Doob's h-transform and Langevin Monte Carlo to decompose the update of an intermediate edited sample into two components: a "reconstruction" term and an "editing" term. This decomposition provides flexibility, allowing the reconstruction term to be computed via existing inversion techniques and enabling the combination of multiple editing terms to handle complex editing tasks. To our knowledge, h-Edit is the first training-free method capable of performing simultaneous text-guided and reward-model-based editing. Extensive experiments, both quantitative and qualitative, show that h-Edit outperforms state-of-the-art baselines in terms of editing effectiveness and faithfulness. Our source code is available at https://github.com/nktoan/h-edit.

Amortized Conditional Independence Testing

Testing for the conditional independence structure in data is a fundamental and critical task in statistics and machine learning, which finds natural applications in causal discovery - a highly relevant problem to many scientific disciplines. Existing methods seek to design explicit test statistics that quantify the degree of conditional dependence, which is highly challenging yet cannot capture nor utilize prior knowledge in a data-driven manner. In this study, an entirely new approach is introduced, where we instead propose to amortize conditional independence testing and devise ACID - a novel transformer-based neural network architecture that learns to test for conditional independence. ACID can be trained on synthetic data in a supervised learning fashion, and the learned model can then be applied to any dataset of similar natures or adapted to new domains by fine-tuning with a negligible computational cost. Our extensive empirical evaluations on both synthetic and real data reveal that ACID consistently achieves state-of-the-art performance against existing baselines under multiple metrics, and is able to generalize robustly to unseen sample sizes, dimensionalities, as well as non-linearities with a remarkably low inference time.

Causal Discovery via Bayesian Optimization

Existing score-based methods for directed acyclic graph (DAG) learning from observational data struggle to recover the causal graph accurately and sample-efficiently. To overcome this, in this study, we propose DrBO (DAG recovery via Bayesian Optimization)-a novel DAG learning framework leveraging Bayesian optimization (BO) to find high-scoring DAGs. We show that, by sophisticatedly choosing the promising DAGs to explore, we can find higher-scoring ones much more efficiently. To address the scalability issues of conventional BO in DAG learning, we replace Gaussian Processes commonly employed in BO with dropout neural networks, trained in a continual manner, which allows for (i) flexibly modeling the DAG scores without overfitting, (ii) incorporation of uncertainty into the estimated scores, and (iii) scaling with the number of evaluations. As a result, DrBO is computationally efficient and can find the accurate DAG in fewer trials and less time than existing state-of-the-art methods. This is demonstrated through an extensive set of empirical evaluations on many challenging settings with both synthetic and real data. Our implementation is available at https://github.com/baosws/DrBO.

Generating Realistic Tabular Data with Large Language Models

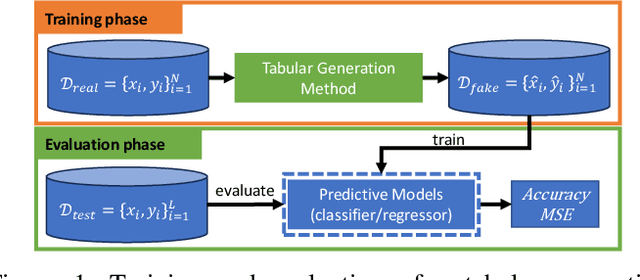
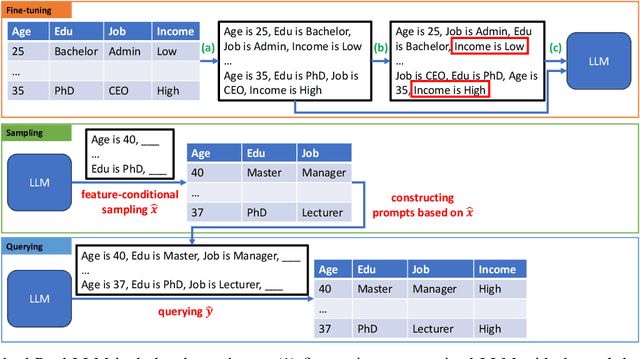
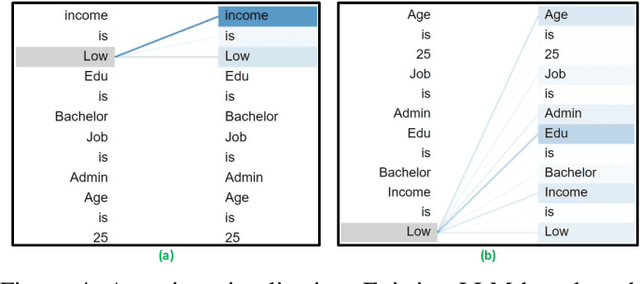
While most generative models show achievements in image data generation, few are developed for tabular data generation. Recently, due to success of large language models (LLM) in diverse tasks, they have also been used for tabular data generation. However, these methods do not capture the correct correlation between the features and the target variable, hindering their applications in downstream predictive tasks. To address this problem, we propose a LLM-based method with three important improvements to correctly capture the ground-truth feature-class correlation in the real data. First, we propose a novel permutation strategy for the input data in the fine-tuning phase. Second, we propose a feature-conditional sampling approach to generate synthetic samples. Finally, we generate the labels by constructing prompts based on the generated samples to query our fine-tuned LLM. Our extensive experiments show that our method significantly outperforms 10 SOTA baselines on 20 datasets in downstream tasks. It also produces highly realistic synthetic samples in terms of quality and diversity. More importantly, classifiers trained with our synthetic data can even compete with classifiers trained with the original data on half of the benchmark datasets, which is a significant achievement in tabular data generation.

ALIAS: DAG Learning with Efficient Unconstrained Policies

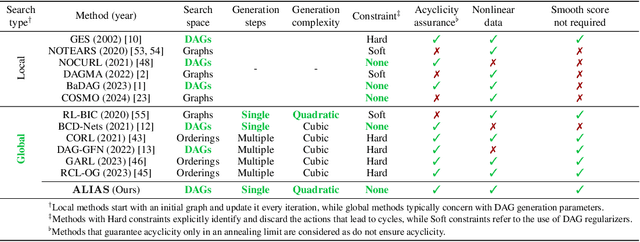
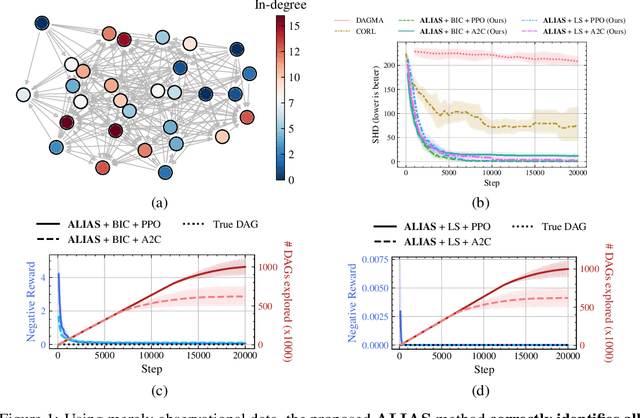
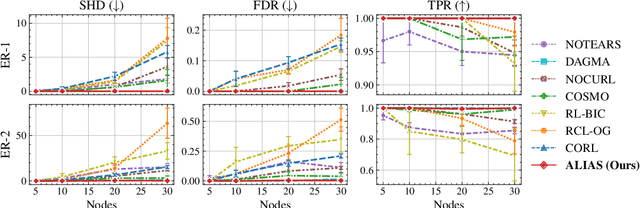
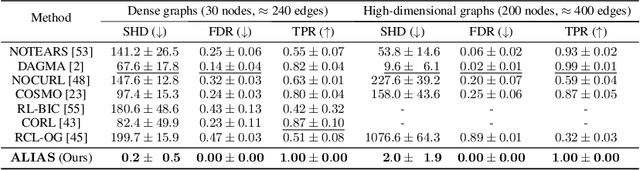
Recently, reinforcement learning (RL) has proved a promising alternative for conventional local heuristics in score-based approaches to learning directed acyclic causal graphs (DAGs) from observational data. However, the intricate acyclicity constraint still challenges the efficient exploration of the vast space of DAGs in existing methods. In this study, we introduce ALIAS (reinforced dAg Learning wIthout Acyclicity conStraints), a novel approach to causal discovery powered by the RL machinery. Our method features an efficient policy for generating DAGs in just a single step with an optimal quadratic complexity, fueled by a novel parametrization of DAGs that directly translates a continuous space to the space of all DAGs, bypassing the need for explicitly enforcing acyclicity constraints. This approach enables us to navigate the search space more effectively by utilizing policy gradient methods and established scoring functions. In addition, we provide compelling empirical evidence for the strong performance of ALIAS in comparison with state-of-the-arts in causal discovery over increasingly difficult experiment conditions on both synthetic and real datasets.

Enabling Causal Discovery in Post-Nonlinear Models with Normalizing Flows

Post-nonlinear (PNL) causal models stand out as a versatile and adaptable framework for modeling intricate causal relationships. However, accurately capturing the invertibility constraint required in PNL models remains challenging in existing studies. To address this problem, we introduce CAF-PoNo (Causal discovery via Normalizing Flows for Post-Nonlinear models), harnessing the power of the normalizing flows architecture to enforce the crucial invertibility constraint in PNL models. Through normalizing flows, our method precisely reconstructs the hidden noise, which plays a vital role in cause-effect identification through statistical independence testing. Furthermore, the proposed approach exhibits remarkable extensibility, as it can be seamlessly expanded to facilitate multivariate causal discovery via causal order identification, empowering us to efficiently unravel complex causal relationships. Extensive experimental evaluations on both simulated and real datasets consistently demonstrate that the proposed method outperforms several state-of-the-art approaches in both bivariate and multivariate causal discovery tasks.

Scalable Variational Causal Discovery Unconstrained by Acyclicity

Bayesian causal discovery offers the power to quantify epistemic uncertainties among a broad range of structurally diverse causal theories potentially explaining the data, represented in forms of directed acyclic graphs (DAGs). However, existing methods struggle with efficient DAG sampling due to the complex acyclicity constraint. In this study, we propose a scalable Bayesian approach to effectively learn the posterior distribution over causal graphs given observational data thanks to the ability to generate DAGs without explicitly enforcing acyclicity. Specifically, we introduce a novel differentiable DAG sampling method that can generate a valid acyclic causal graph by mapping an unconstrained distribution of implicit topological orders to a distribution over DAGs. Given this efficient DAG sampling scheme, we are able to model the posterior distribution over causal graphs using a simple variational distribution over a continuous domain, which can be learned via the variational inference framework. Extensive empirical experiments on both simulated and real datasets demonstrate the superior performance of the proposed model compared to several state-of-the-art baselines.

Variational Flow Models: Flowing in Your Style

We introduce a variational inference interpretation for models of "posterior flows" - generalizations of "probability flows" to a broader class of stochastic processes not necessarily diffusion processes. We coin the resulting models as "Variational Flow Models". Additionally, we propose a systematic training-free method to transform the posterior flow of a "linear" stochastic process characterized by the equation Xt = at * X0 + st * X1 into a straight constant-speed (SC) flow, reminiscent of Rectified Flow. This transformation facilitates fast sampling along the original posterior flow without training a new model of the SC flow. The flexibility of our approach allows us to extend our transformation to inter-convert two posterior flows from distinct "linear" stochastic processes. Moreover, we can easily integrate high-order numerical solvers into the transformed SC flow, further enhancing sampling accuracy and efficiency. Rigorous theoretical analysis and extensive experimental results substantiate the advantages of our framework.