DmC: Nearest Neighbor Guidance Diffusion Model for Offline Cross-domain Reinforcement Learning

Cross-domain offline reinforcement learning (RL) seeks to enhance sample efficiency in offline RL by utilizing additional offline source datasets. A key challenge is to identify and utilize source samples that are most relevant to the target domain. Existing approaches address this challenge by measuring domain gaps through domain classifiers, target transition dynamics modeling, or mutual information estimation using contrastive loss. However, these methods often require large target datasets, which is impractical in many real-world scenarios. In this work, we address cross-domain offline RL under a limited target data setting, identifying two primary challenges: (1) Dataset imbalance, which is caused by large source and small target datasets and leads to overfitting in neural network-based domain gap estimators, resulting in uninformative measurements; and (2) Partial domain overlap, where only a subset of the source data is closely aligned with the target domain. To overcome these issues, we propose DmC, a novel framework for cross-domain offline RL with limited target samples. Specifically, DmC utilizes $k$-nearest neighbor ($k$-NN) based estimation to measure domain proximity without neural network training, effectively mitigating overfitting. Then, by utilizing this domain proximity, we introduce a nearest-neighbor-guided diffusion model to generate additional source samples that are better aligned with the target domain, thus enhancing policy learning with more effective source samples. Through theoretical analysis and extensive experiments in diverse MuJoCo environments, we demonstrate that DmC significantly outperforms state-of-the-art cross-domain offline RL methods, achieving substantial performance gains.

h-Edit: Effective and Flexible Diffusion-Based Editing via Doob's h-Transform

We introduce a theoretical framework for diffusion-based image editing by formulating it as a reverse-time bridge modeling problem. This approach modifies the backward process of a pretrained diffusion model to construct a bridge that converges to an implicit distribution associated with the editing target at time 0. Building on this framework, we propose h-Edit, a novel editing method that utilizes Doob's h-transform and Langevin Monte Carlo to decompose the update of an intermediate edited sample into two components: a "reconstruction" term and an "editing" term. This decomposition provides flexibility, allowing the reconstruction term to be computed via existing inversion techniques and enabling the combination of multiple editing terms to handle complex editing tasks. To our knowledge, h-Edit is the first training-free method capable of performing simultaneous text-guided and reward-model-based editing. Extensive experiments, both quantitative and qualitative, show that h-Edit outperforms state-of-the-art baselines in terms of editing effectiveness and faithfulness. Our source code is available at https://github.com/nktoan/h-edit.

TEAM: Topological Evolution-aware Framework for Traffic Forecasting--Extended Version

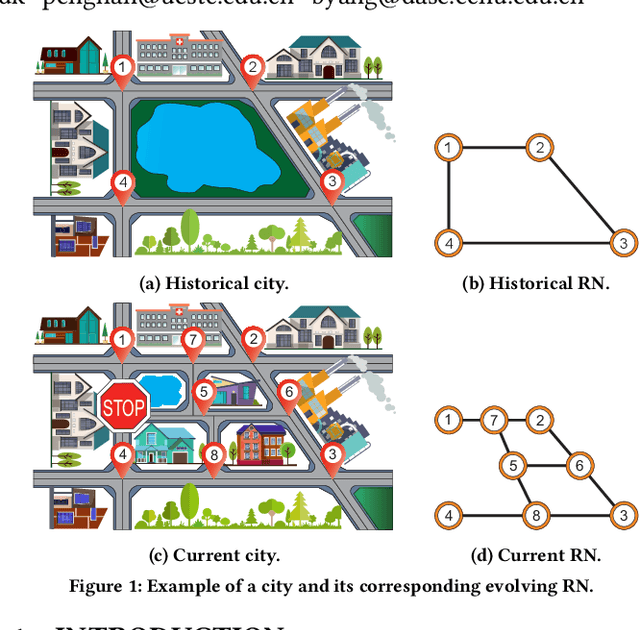
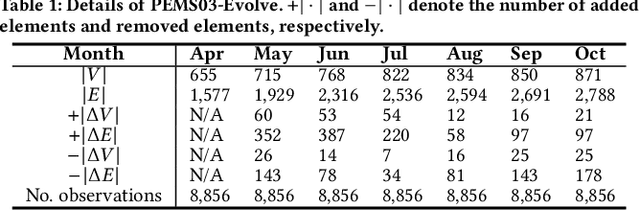
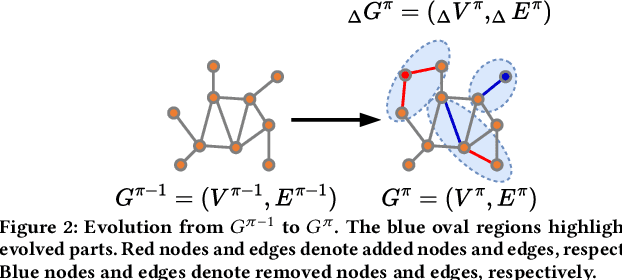
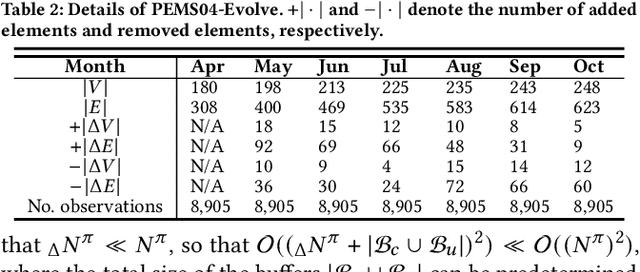
Due to the global trend towards urbanization, people increasingly move to and live in cities that then continue to grow. Traffic forecasting plays an important role in the intelligent transportation systems of cities as well as in spatio-temporal data mining. State-of-the-art forecasting is achieved by deep-learning approaches due to their ability to contend with complex spatio-temporal dynamics. However, existing methods assume the input is fixed-topology road networks and static traffic time series. These assumptions fail to align with urbanization, where time series are collected continuously and road networks evolve over time. In such settings, deep-learning models require frequent re-initialization and re-training, imposing high computational costs. To enable much more efficient training without jeopardizing model accuracy, we propose the Topological Evolution-aware Framework (TEAM) for traffic forecasting that incorporates convolution and attention. This combination of mechanisms enables better adaptation to newly collected time series, while being able to maintain learned knowledge from old time series. TEAM features a continual learning module based on the Wasserstein metric that acts as a buffer that can identify the most stable and the most changing network nodes. Then, only data related to stable nodes is employed for re-training when consolidating a model. Further, only data of new nodes and their adjacent nodes as well as data pertaining to changing nodes are used to re-train the model. Empirical studies with two real-world traffic datasets offer evidence that TEAM is capable of much lower re-training costs than existing methods are, without jeopardizing forecasting accuracy.

Variational Flow Models: Flowing in Your Style

We introduce a variational inference interpretation for models of "posterior flows" - generalizations of "probability flows" to a broader class of stochastic processes not necessarily diffusion processes. We coin the resulting models as "Variational Flow Models". Additionally, we propose a systematic training-free method to transform the posterior flow of a "linear" stochastic process characterized by the equation Xt = at * X0 + st * X1 into a straight constant-speed (SC) flow, reminiscent of Rectified Flow. This transformation facilitates fast sampling along the original posterior flow without training a new model of the SC flow. The flexibility of our approach allows us to extend our transformation to inter-convert two posterior flows from distinct "linear" stochastic processes. Moreover, we can easily integrate high-order numerical solvers into the transformed SC flow, further enhancing sampling accuracy and efficiency. Rigorous theoretical analysis and extensive experimental results substantiate the advantages of our framework.