Revisiting the Dataset Bias Problem from a Statistical Perspective

In this paper, we study the "dataset bias" problem from a statistical standpoint, and identify the main cause of the problem as the strong correlation between a class attribute u and a non-class attribute b in the input x, represented by p(u|b) differing significantly from p(u). Since p(u|b) appears as part of the sampling distributions in the standard maximum log-likelihood (MLL) objective, a model trained on a biased dataset via MLL inherently incorporates such correlation into its parameters, leading to poor generalization to unbiased test data. From this observation, we propose to mitigate dataset bias via either weighting the objective of each sample n by \frac{1}{p(u_{n}|b_{n})} or sampling that sample with a weight proportional to \frac{1}{p(u_{n}|b_{n})}. While both methods are statistically equivalent, the former proves more stable and effective in practice. Additionally, we establish a connection between our debiasing approach and causal reasoning, reinforcing our method's theoretical foundation. However, when the bias label is unavailable, computing p(u|b) exactly is difficult. To overcome this challenge, we propose to approximate \frac{1}{p(u|b)} using a biased classifier trained with "bias amplification" losses. Extensive experiments on various biased datasets demonstrate the superiority of our method over existing debiasing techniques in most settings, validating our theoretical analysis.

Towards the new XAI: A Hypothesis-Driven Approach to Decision Support Using Evidence

Prior research on AI-assisted human decision-making has explored several different explainable AI (XAI) approaches. A recent paper has proposed a paradigm shift calling for hypothesis-driven XAI through a conceptual framework called evaluative AI that gives people evidence that supports or refutes hypotheses without necessarily giving a decision-aid recommendation. In this paper we describe and evaluate an approach for hypothesis-driven XAI based on the Weight of Evidence (WoE) framework, which generates both positive and negative evidence for a given hypothesis. Through human behavioural experiments, we show that our hypothesis-driven approach increases decision accuracy, reduces reliance compared to a recommendation-driven approach and an AI-explanation-only baseline, but with a small increase in under-reliance compared to the recommendation-driven approach. Further, we show that participants used our hypothesis-driven approach in a materially different way to the two baselines.

Explaining Model Confidence Using Counterfactuals

Displaying confidence scores in human-AI interaction has been shown to help build trust between humans and AI systems. However, most existing research uses only the confidence score as a form of communication. As confidence scores are just another model output, users may want to understand why the algorithm is confident to determine whether to accept the confidence score. In this paper, we show that counterfactual explanations of confidence scores help study participants to better understand and better trust a machine learning model's prediction. We present two methods for understanding model confidence using counterfactual explanation: (1) based on counterfactual examples; and (2) based on visualisation of the counterfactual space. Both increase understanding and trust for study participants over a baseline of no explanation, but qualitative results show that they are used quite differently, leading to recommendations of when to use each one and directions of designing better explanations.

Improving Model Understanding and Trust with Counterfactual Explanations of Model Confidence

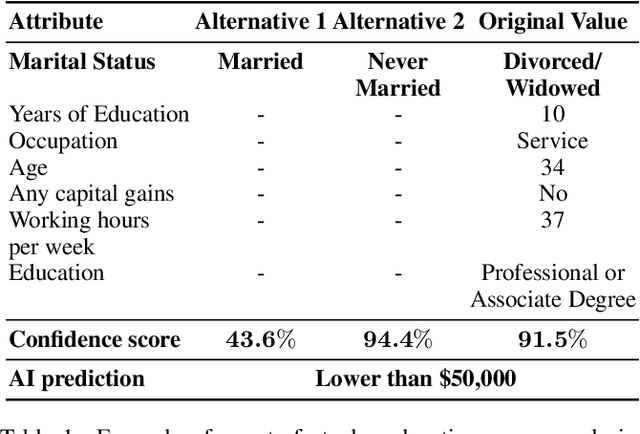
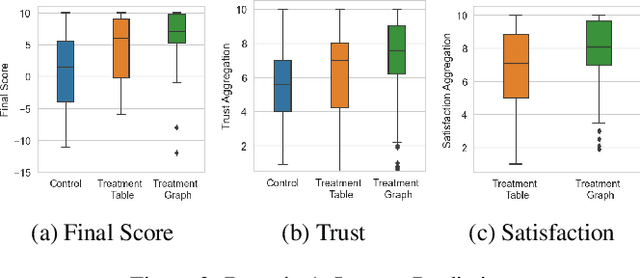
In this paper, we show that counterfactual explanations of confidence scores help users better understand and better trust an AI model's prediction in human-subject studies. Showing confidence scores in human-agent interaction systems can help build trust between humans and AI systems. However, most existing research only used the confidence score as a form of communication, and we still lack ways to explain why the algorithm is confident. This paper also presents two methods for understanding model confidence using counterfactual explanation: (1) based on counterfactual examples; and (2) based on visualisation of the counterfactual space.