Entropy-regularized Point-based Value Iteration

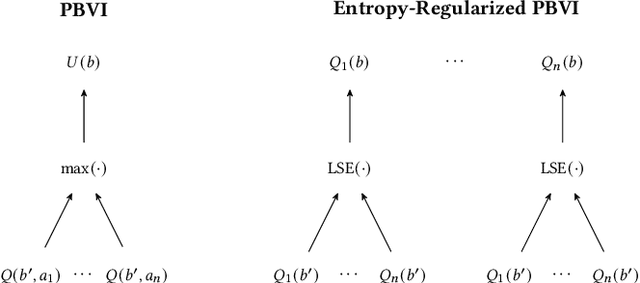
Model-based planners for partially observable problems must accommodate both model uncertainty during planning and goal uncertainty during objective inference. However, model-based planners may be brittle under these types of uncertainty because they rely on an exact model and tend to commit to a single optimal behavior. Inspired by results in the model-free setting, we propose an entropy-regularized model-based planner for partially observable problems. Entropy regularization promotes policy robustness for planning and objective inference by encouraging policies to be no more committed to a single action than necessary. We evaluate the robustness and objective inference performance of entropy-regularized policies in three problem domains. Our results show that entropy-regularized policies outperform non-entropy-regularized baselines in terms of higher expected returns under modeling errors and higher accuracy during objective inference.

Learning to Optimize Autonomy in Competence-Aware Systems

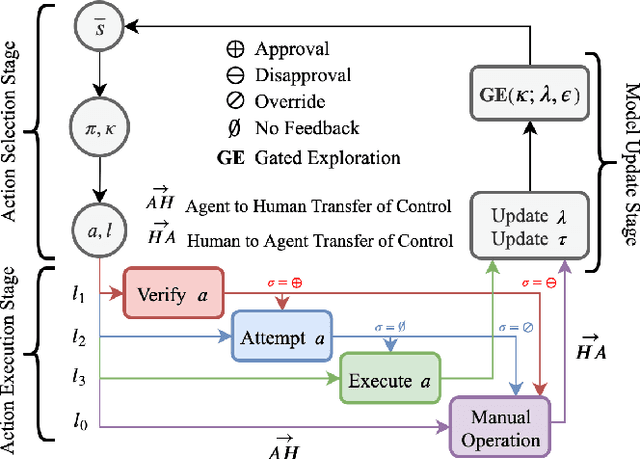
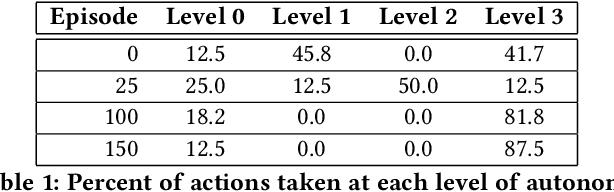
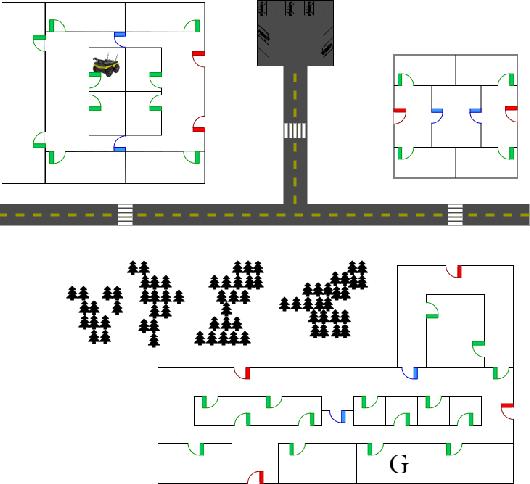
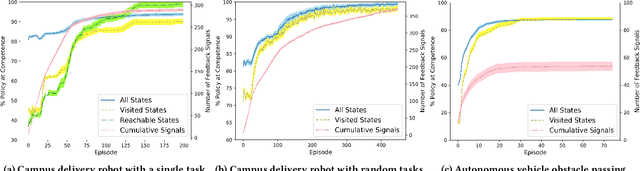
Interest in semi-autonomous systems (SAS) is growing rapidly as a paradigm to deploy autonomous systems in domains that require occasional reliance on humans. This paradigm allows service robots or autonomous vehicles to operate at varying levels of autonomy and offer safety in situations that require human judgment. We propose an introspective model of autonomy that is learned and updated online through experience and dictates the extent to which the agent can act autonomously in any given situation. We define a competence-aware system (CAS) that explicitly models its own proficiency at different levels of autonomy and the available human feedback. A CAS learns to adjust its level of autonomy based on experience to maximize overall efficiency, factoring in the cost of human assistance. We analyze the convergence properties of CAS and provide experimental results for robot delivery and autonomous driving domains that demonstrate the benefits of the approach.

A Sufficient Statistic for Influence in Structured Multiagent Environments

Making decisions in complex environments is a key challenge in artificial intelligence (AI). Situations involving multiple decision makers are particularly complex, leading to computation intractability of principled solution methods. A body of work in AI [4, 3, 41, 45, 47, 2] has tried to mitigate this problem by trying to bring down interaction to its core: how does the policy of one agent influence another agent? If we can find more compact representations of such influence, this can help us deal with the complexity, for instance by searching the space of influences rather than that of policies [45]. However, so far these notions of influence have been restricted in their applicability to special cases of interaction. In this paper we formalize influence-based abstraction (IBA), which facilitates the elimination of latent state factors without any loss in value, for a very general class of problems described as factored partially observable stochastic games (fPOSGs) [33]. This generalizes existing descriptions of influence, and thus can serve as the foundation for improvements in scalability and other insights in decision making in complex settings.

Influence-Optimistic Local Values for Multiagent Planning --- Extended Version

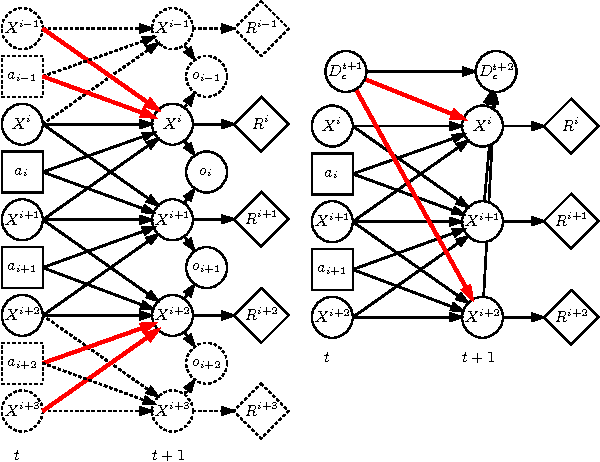
Recent years have seen the development of methods for multiagent planning under uncertainty that scale to tens or even hundreds of agents. However, most of these methods either make restrictive assumptions on the problem domain, or provide approximate solutions without any guarantees on quality. Methods in the former category typically build on heuristic search using upper bounds on the value function. Unfortunately, no techniques exist to compute such upper bounds for problems with non-factored value functions. To allow for meaningful benchmarking through measurable quality guarantees on a very general class of problems, this paper introduces a family of influence-optimistic upper bounds for factored decentralized partially observable Markov decision processes (Dec-POMDPs) that do not have factored value functions. Intuitively, we derive bounds on very large multiagent planning problems by subdividing them in sub-problems, and at each of these sub-problems making optimistic assumptions with respect to the influence that will be exerted by the rest of the system. We numerically compare the different upper bounds and demonstrate how we can achieve a non-trivial guarantee that a heuristic solution for problems with hundreds of agents is close to optimal. Furthermore, we provide evidence that the upper bounds may improve the effectiveness of heuristic influence search, and discuss further potential applications to multiagent planning.