MARBLE: Multi-Armed Restless Bandits in Latent Markovian Environment

Restless Multi-Armed Bandits (RMABs) are powerful models for decision-making under uncertainty, yet classical formulations typically assume fixed dynamics, an assumption often violated in nonstationary environments. We introduce MARBLE (Multi-Armed Restless Bandits in a Latent Markovian Environment), which augments RMABs with a latent Markov state that induces nonstationary behavior. In MARBLE, each arm evolves according to a latent environment state that switches over time, making policy learning substantially more challenging. We further introduce the Markov-Averaged Indexability (MAI) criterion as a relaxed indexability assumption and prove that, despite unobserved regime switches, under the MAI criterion, synchronous Q-learning with Whittle Indices (QWI) converges almost surely to the optimal Q-function and the corresponding Whittle indices. We validate MARBLE on a calibrated simulator-embedded (digital twin) recommender system, where QWI consistently adapts to a shifting latent state and converges to an optimal policy, empirically corroborating our theoretical findings.

Challenger-Based Combinatorial Bandits for Subcarrier Selection in OFDM Systems

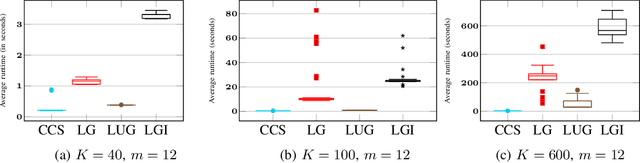
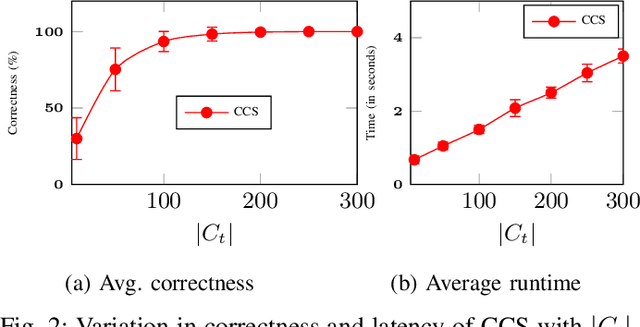
This paper investigates the identification of the top-m user-scheduling sets in multi-user MIMO downlink, which is cast as a combinatorial pure-exploration problem in stochastic linear bandits. Because the action space grows exponentially, exhaustive search is infeasible. We therefore adopt a linear utility model to enable efficient exploration and reliable selection of promising user subsets. We introduce a gap-index framework that maintains a shortlist of current estimates of champion arms (top-m sets) and a rotating shortlist of challenger arms that pose the greatest threat to the champions. This design focuses on measurements that yield the most informative gap-index-based comparisons, resulting in significant reductions in runtime and computation compared to state-of-the-art linear bandit methods, with high identification accuracy. The method also exposes a tunable trade-off between speed and accuracy. Simulations on a realistic OFDM downlink show that shortlist-driven pure exploration makes online, measurement-efficient subcarrier selection practical for AI-enabled communication systems.

Adaptive Budgeted Multi-Armed Bandits for IoT with Dynamic Resource Constraints

Internet of Things (IoT) systems increasingly operate in environments where devices must respond in real time while managing fluctuating resource constraints, including energy and bandwidth. Yet, current approaches often fall short in addressing scenarios where operational constraints evolve over time. To address these limitations, we propose a novel Budgeted Multi-Armed Bandit framework tailored for IoT applications with dynamic operational limits. Our model introduces a decaying violation budget, which permits limited constraint violations early in the learning process and gradually enforces stricter compliance over time. We present the Budgeted Upper Confidence Bound (UCB) algorithm, which adaptively balances performance optimization and compliance with time-varying constraints. We provide theoretical guarantees showing that Budgeted UCB achieves sublinear regret and logarithmic constraint violations over the learning horizon. Extensive simulations in a wireless communication setting show that our approach achieves faster adaptation and better constraint satisfaction than standard online learning methods. These results highlight the framework's potential for building adaptive, resource-aware IoT systems.

Dynamic and Distributed Routing in IoT Networks based on Multi-Objective Q-Learning

The last few decades have witnessed a rapid increase in IoT devices owing to their wide range of applications, such as smart healthcare monitoring systems, smart cities, and environmental monitoring. A critical task in IoT networks is sensing and transmitting information over the network. The IoT nodes gather data by sensing the environment and then transmit this data to a destination node via multi-hop communication, following some routing protocols. These protocols are usually designed to optimize possibly contradictory objectives, such as maximizing packet delivery ratio and energy efficiency. While most literature has focused on optimizing a static objective that remains unchanged, many real-world IoT applications require adapting to rapidly shifting priorities. For example, in monitoring systems, some transmissions are time-critical and require a high priority on low latency, while other transmissions are less urgent and instead prioritize energy efficiency. To meet such dynamic demands, we propose novel dynamic and distributed routing based on multiobjective Q-learning that can adapt to changes in preferences in real-time. Our algorithm builds on ideas from both multi-objective optimization and Q-learning. We also propose a novel greedy interpolation policy scheme to take near-optimal decisions for unexpected preference changes. The proposed scheme can approximate and utilize the Pareto-efficient solutions for dynamic preferences, thus utilizing past knowledge to adapt to unpredictable preferences quickly during runtime. Simulation results show that the proposed scheme outperforms state-of-the-art algorithms for various exploration strategies, preference variation patterns, and important metrics like overall reward, energy efficiency, and packet delivery ratio.

Reinforcement Learning in Switching Non-Stationary Markov Decision Processes: Algorithms and Convergence Analysis

Reinforcement learning in non-stationary environments is challenging due to abrupt and unpredictable changes in dynamics, often causing traditional algorithms to fail to converge. However, in many real-world cases, non-stationarity has some structure that can be exploited to develop algorithms and facilitate theoretical analysis. We introduce one such structure, Switching Non-Stationary Markov Decision Processes (SNS-MDP), where environments switch over time based on an underlying Markov chain. Under a fixed policy, the value function of an SNS-MDP admits a closed-form solution determined by the Markov chain's statistical properties, and despite the inherent non-stationarity, Temporal Difference (TD) learning methods still converge to the correct value function. Furthermore, policy improvement can be performed, and it is shown that policy iteration converges to the optimal policy. Moreover, since Q-learning converges to the optimal Q-function, it likewise yields the corresponding optimal policy. To illustrate the practical advantages of SNS-MDPs, we present an example in communication networks where channel noise follows a Markovian pattern, demonstrating how this framework can effectively guide decision-making in complex, time-varying contexts.

Benchmarking Dynamic SLO Compliance in Distributed Computing Continuum Systems

Ensuring Service Level Objectives (SLOs) in large-scale architectures, such as Distributed Computing Continuum Systems (DCCS), is challenging due to their heterogeneous nature and varying service requirements across different devices and applications. Additionally, unpredictable workloads and resource limitations lead to fluctuating performance and violated SLOs. To improve SLO compliance in DCCS, one possibility is to apply machine learning; however, the design choices are often left to the developer. To that extent, we provide a benchmark of Active Inference -- an emerging method from neuroscience -- against three established reinforcement learning algorithms (Deep Q-Network, Advantage Actor-Critic, and Proximal Policy Optimization). We consider a realistic DCCS use case: an edge device running a video conferencing application alongside a WebSocket server streaming videos. Using one of the respective algorithms, we continuously monitor key performance metrics, such as latency and bandwidth usage, to dynamically adjust parameters -- including the number of streams, frame rate, and resolution -- to optimize service quality and user experience. To test algorithms' adaptability to constant system changes, we simulate dynamically changing SLOs and both instant and gradual data-shift scenarios, such as network bandwidth limitations and fluctuating device thermal states. Although the evaluated algorithms all showed advantages and limitations, our findings demonstrate that Active Inference is a promising approach for ensuring SLO compliance in DCCS, offering lower memory usage, stable CPU utilization, and fast convergence.

Distributed Momentum Methods Under Biased Gradient Estimations

Distributed stochastic gradient methods are gaining prominence in solving large-scale machine learning problems that involve data distributed across multiple nodes. However, obtaining unbiased stochastic gradients, which have been the focus of most theoretical research, is challenging in many distributed machine learning applications. The gradient estimations easily become biased, for example, when gradients are compressed or clipped, when data is shuffled, and in meta-learning and reinforcement learning. In this work, we establish non-asymptotic convergence bounds on distributed momentum methods under biased gradient estimation on both general non-convex and $\mu$-PL non-convex problems. Our analysis covers general distributed optimization problems, and we work out the implications for special cases where gradient estimates are biased, i.e., in meta-learning and when the gradients are compressed or clipped. Our numerical experiments on training deep neural networks with Top-$K$ sparsification and clipping verify faster convergence performance of momentum methods than traditional biased gradient descent.

On the Convergence of Federated Learning Algorithms without Data Similarity

Data similarity assumptions have traditionally been relied upon to understand the convergence behaviors of federated learning methods. Unfortunately, this approach often demands fine-tuning step sizes based on the level of data similarity. When data similarity is low, these small step sizes result in an unacceptably slow convergence speed for federated methods. In this paper, we present a novel and unified framework for analyzing the convergence of federated learning algorithms without the need for data similarity conditions. Our analysis centers on an inequality that captures the influence of step sizes on algorithmic convergence performance. By applying our theorems to well-known federated algorithms, we derive precise expressions for three widely used step size schedules: fixed, diminishing, and step-decay step sizes, which are independent of data similarity conditions. Finally, we conduct comprehensive evaluations of the performance of these federated learning algorithms, employing the proposed step size strategies to train deep neural network models on benchmark datasets under varying data similarity conditions. Our findings demonstrate significant improvements in convergence speed and overall performance, marking a substantial advancement in federated learning research.

SCANIA Component X Dataset: A Real-World Multivariate Time Series Dataset for Predictive Maintenance

This paper presents a description of a real-world, multivariate time series dataset collected from an anonymized engine component (called Component X) of a fleet of trucks from SCANIA, Sweden. This dataset includes diverse variables capturing detailed operational data, repair records, and specifications of trucks while maintaining confidentiality by anonymization. It is well-suited for a range of machine learning applications, such as classification, regression, survival analysis, and anomaly detection, particularly when applied to predictive maintenance scenarios. The large population size and variety of features in the format of histograms and numerical counters, along with the inclusion of temporal information, make this real-world dataset unique in the field. The objective of releasing this dataset is to give a broad range of researchers the possibility of working with real-world data from an internationally well-known company and introduce a standard benchmark to the predictive maintenance field, fostering reproducible research.

Human-Inspired Framework to Accelerate Reinforcement Learning

While deep reinforcement learning (RL) is becoming an integral part of good decision-making in data science, it is still plagued with sample inefficiency. This can be challenging when applying deep-RL in real-world environments where physical interactions are expensive and can risk system safety. To improve the sample efficiency of RL algorithms, this paper proposes a novel human-inspired framework that facilitates fast exploration and learning for difficult RL tasks. The main idea is to first provide the learning agent with simpler but similar tasks that gradually grow in difficulty and progress toward the main task. The proposed method requires no pre-training phase. Specifically, the learning of simpler tasks is only done for one iteration. The generated knowledge could be used by any transfer learning, including value transfer and policy transfer, to reduce the sample complexity while not adding to the computational complexity. So, it can be applied to any goal, environment, and reinforcement learning algorithm - both value-based methods and policy-based methods and both tabular methods and deep-RL methods. We have evaluated our proposed framework on both a simple Random Walk for illustration purposes and on more challenging optimal control problems with constraint. The experiments show the good performance of our proposed framework in improving the sample efficiency of RL-learning algorithms, especially when the main task is difficult.