On the Convergence of Step Decay Step-Size for Stochastic Optimization
Paper and Code
Feb 18, 2021


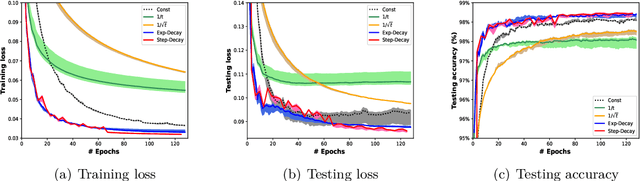
The convergence of stochastic gradient descent is highly dependent on the step-size, especially on non-convex problems such as neural network training. Step decay step-size schedules (constant and then cut) are widely used in practice because of their excellent convergence and generalization qualities, but their theoretical properties are not yet well understood. We provide the convergence results for step decay in the non-convex regime, ensuring that the gradient norm vanishes at an $\mathcal{O}(\ln T/\sqrt{T})$ rate. We also provide the convergence guarantees for general (possibly non-smooth) convex problems, ensuring an $\mathcal{O}(\ln T/\sqrt{T})$ convergence rate. Finally, in the strongly convex case, we establish an $\mathcal{O}(\ln T/T)$ rate for smooth problems, which we also prove to be tight, and an $\mathcal{O}(\ln^2 T /T)$ rate without the smoothness assumption. We illustrate the practical efficiency of the step decay step-size in several large scale deep neural network training tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge