Reinforcement Knowledge Graph Reasoning for Explainable Recommendation

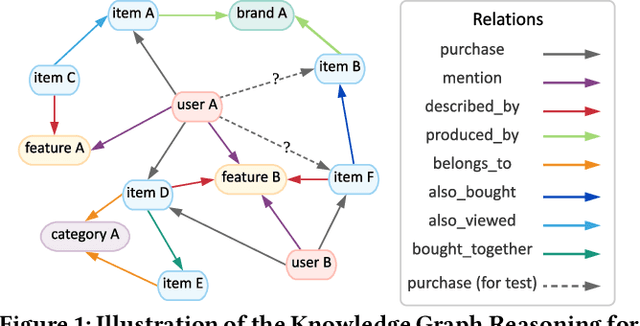
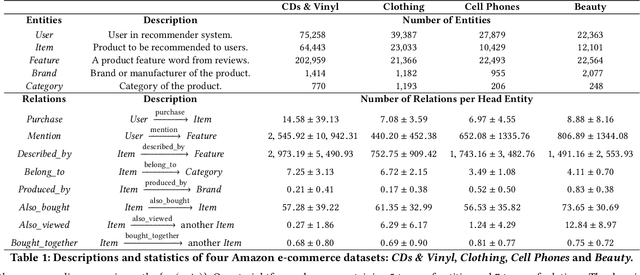
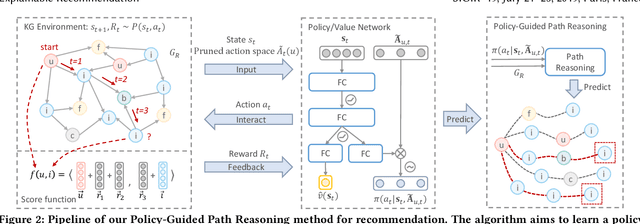
Recent advances in personalized recommendation have sparked great interest in the exploitation of rich structured information provided by knowledge graphs. Unlike most existing approaches that only focus on leveraging knowledge graphs for more accurate recommendation, we perform explicit reasoning with knowledge for decision making so that the recommendations are generated and supported by an interpretable causal inference procedure. To this end, we propose a method called Policy-Guided Path Reasoning (PGPR), which couples recommendation and interpretability by providing actual paths in a knowledge graph. Our contributions include four aspects. We first highlight the significance of incorporating knowledge graphs into recommendation to formally define and interpret the reasoning process. Second, we propose a reinforcement learning (RL) approach featuring an innovative soft reward strategy, user-conditional action pruning and a multi-hop scoring function. Third, we design a policy-guided graph search algorithm to efficiently and effectively sample reasoning paths for recommendation. Finally, we extensively evaluate our method on several large-scale real-world benchmark datasets, obtaining favorable results compared with state-of-the-art methods.

Waterfall Bandits: Learning to Sell Ads Online

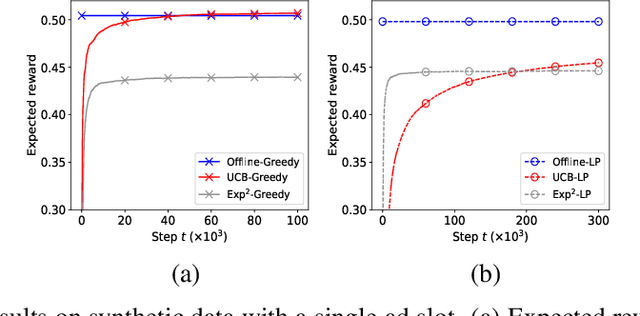
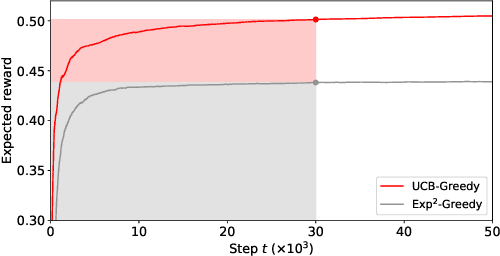
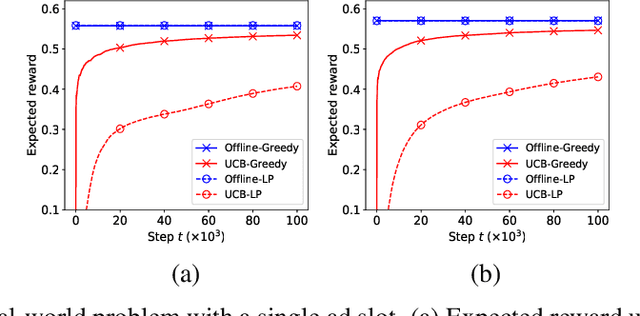
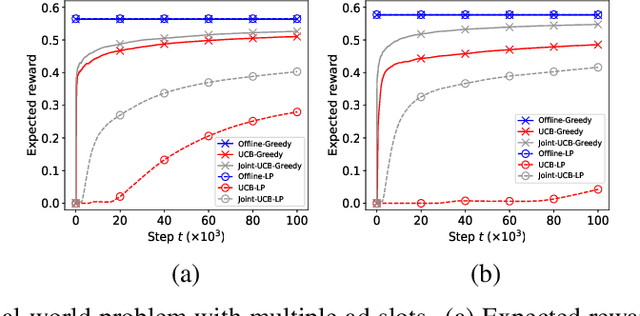
A popular approach to selling online advertising is by a waterfall, where a publisher makes sequential price offers to ad networks for an inventory, and chooses the winner in that order. The publisher picks the order and prices to maximize her revenue. A traditional solution is to learn the demand model and then subsequently solve the optimization problem for the given demand model. This will incur a linear regret. We design an online learning algorithm for solving this problem, which interleaves learning and optimization, and prove that this algorithm has sublinear regret. We evaluate the algorithm on both synthetic and real-world data, and show that it quickly learns high quality pricing strategies. This is the first principled study of learning a waterfall design online by sequential experimentation.

Offline Evaluation of Ranking Policies with Click Models

Many web systems rank and present a list of items to users, from recommender systems to search and advertising. An important problem in practice is to evaluate new ranking policies offline and optimize them before they are deployed. We address this problem by proposing evaluation algorithms for estimating the expected number of clicks on ranked lists from historical logged data. The existing algorithms are not guaranteed to be statistically efficient in our problem because the number of recommended lists can grow exponentially with their length. To overcome this challenge, we use models of user interaction with the list of items, the so-called click models, to construct estimators that learn statistically efficiently. We analyze our estimators and prove that they are more efficient than the estimators that do not use the structure of the click model, under the assumption that the click model holds. We evaluate our estimators in a series of experiments on a real-world dataset and show that they consistently outperform prior estimators.

Stochastic Low-Rank Bandits

Many problems in computer vision and recommender systems involve low-rank matrices. In this work, we study the problem of finding the maximum entry of a stochastic low-rank matrix from sequential observations. At each step, a learning agent chooses pairs of row and column arms, and receives the noisy product of their latent values as a reward. The main challenge is that the latent values are unobserved. We identify a class of non-negative matrices whose maximum entry can be found statistically efficiently and propose an algorithm for finding them, which we call LowRankElim. We derive a $\DeclareMathOperator{\poly}{poly} O((K + L) \poly(d) \Delta^{-1} \log n)$ upper bound on its $n$-step regret, where $K$ is the number of rows, $L$ is the number of columns, $d$ is the rank of the matrix, and $\Delta$ is the minimum gap. The bound depends on other problem-specific constants that clearly do not depend $K L$. To the best of our knowledge, this is the first such result in the literature.

Graphical Model Sketch

Structured high-cardinality data arises in many domains, and poses a major challenge for both modeling and inference. Graphical models are a popular approach to modeling structured data but they are unsuitable for high-cardinality variables. The count-min (CM) sketch is a popular approach to estimating probabilities in high-cardinality data but it does not scale well beyond a few variables. In this work, we bring together the ideas of graphical models and count sketches; and propose and analyze several approaches to estimating probabilities in structured high-cardinality streams of data. The key idea of our approximations is to use the structure of a graphical model and approximately estimate its factors by "sketches", which hash high-cardinality variables using random projections. Our approximations are computationally efficient and their space complexity is independent of the cardinality of variables. Our error bounds are multiplicative and significantly improve upon those of the CM sketch, a state-of-the-art approach to estimating probabilities in streams. We evaluate our approximations on synthetic and real-world problems, and report an order of magnitude improvements over the CM sketch.