Surgical Scheduling via Optimization and Machine Learning with Long-Tailed Data

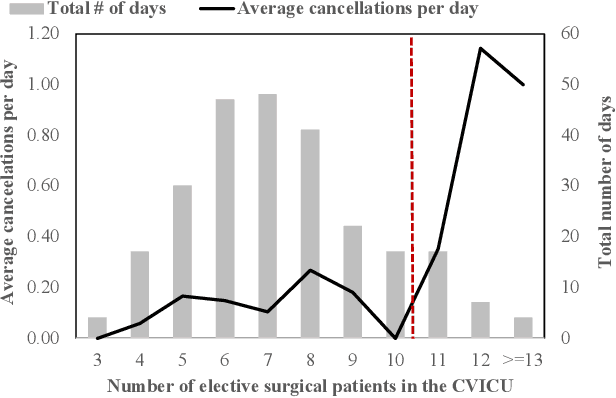
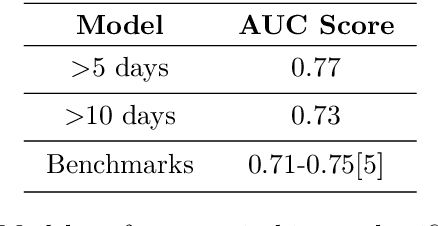
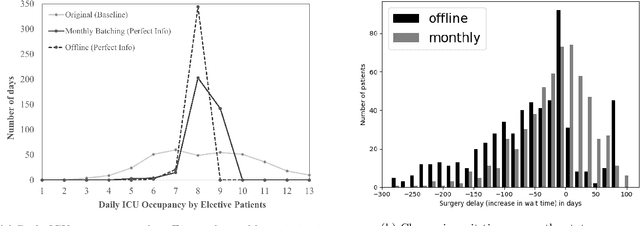
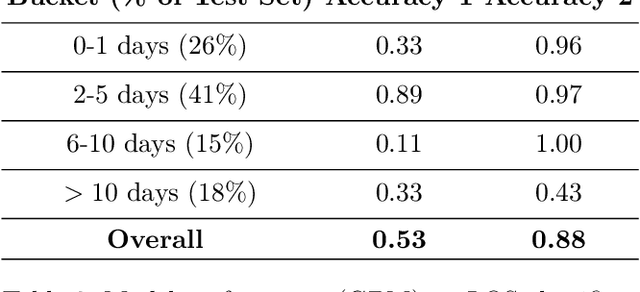
Using data from cardiovascular surgery patients with long and highly variable post-surgical lengths of stay (LOS), we develop a model to reduce recovery unit congestion. We estimate LOS using a variety of machine learning models, schedule procedures with a variety of online optimization models, and estimate performance with simulation. The machine learning models achieved only modest LOS prediction accuracy, despite access to a very rich set of patient characteristics. Compared to the current paper-based system used in the hospital, most optimization models failed to reduce congestion without increasing wait times for surgery. A conservative stochastic optimization with sufficient sampling to capture the long tail of the LOS distribution outperformed the current manual process. These results highlight the perils of using oversimplified distributional models of patient length of stay for scheduling procedures and the importance of using stochastic optimization well-suited to dealing with long-tailed behavior.

Optimal Transport Relaxations with Application to Wasserstein GANs

We propose a family of relaxations of the optimal transport problem which regularize the problem by introducing an additional minimization step over a small region around one of the underlying transporting measures. The type of regularization that we obtain is related to smoothing techniques studied in the optimization literature. When using our approach to estimate optimal transport costs based on empirical measures, we obtain statistical learning bounds which are useful to guide the amount of regularization, while maintaining good generalization properties. To illustrate the computational advantages of our regularization approach, we apply our method to training Wasserstein GANs. We obtain running time improvements, relative to current benchmarks, with no deterioration in testing performance (via FID). The running time improvement occurs because our new optimality-based threshold criterion reduces the number of expensive iterates of the generating networks, while increasing the number of actor-critic iterations.

Waterfall Bandits: Learning to Sell Ads Online

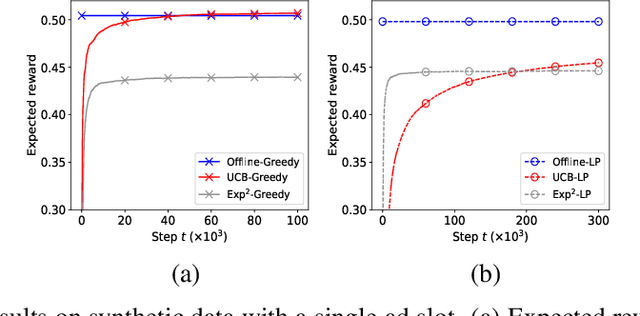
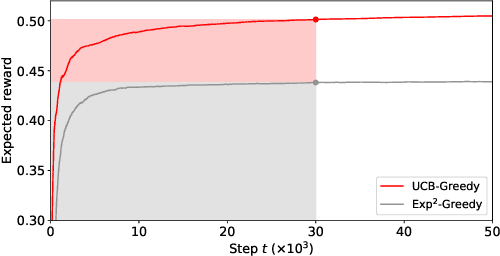
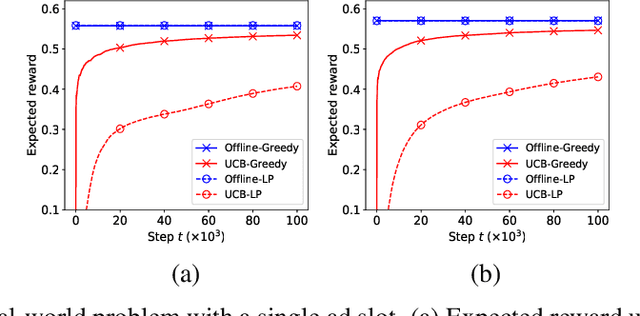
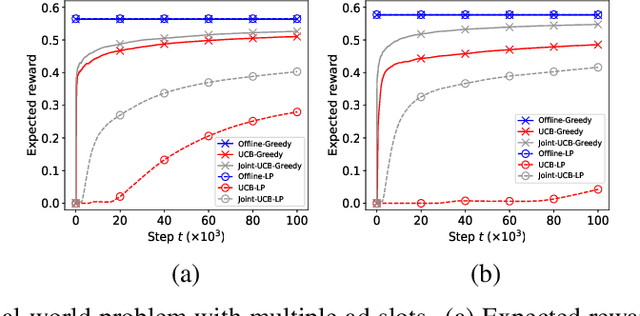
A popular approach to selling online advertising is by a waterfall, where a publisher makes sequential price offers to ad networks for an inventory, and chooses the winner in that order. The publisher picks the order and prices to maximize her revenue. A traditional solution is to learn the demand model and then subsequently solve the optimization problem for the given demand model. This will incur a linear regret. We design an online learning algorithm for solving this problem, which interleaves learning and optimization, and prove that this algorithm has sublinear regret. We evaluate the algorithm on both synthetic and real-world data, and show that it quickly learns high quality pricing strategies. This is the first principled study of learning a waterfall design online by sequential experimentation.