An Interactive Greedy Approach to Group Sparsity in High Dimensions

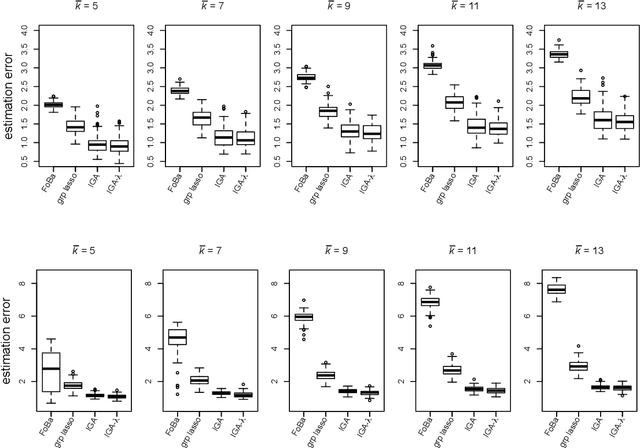
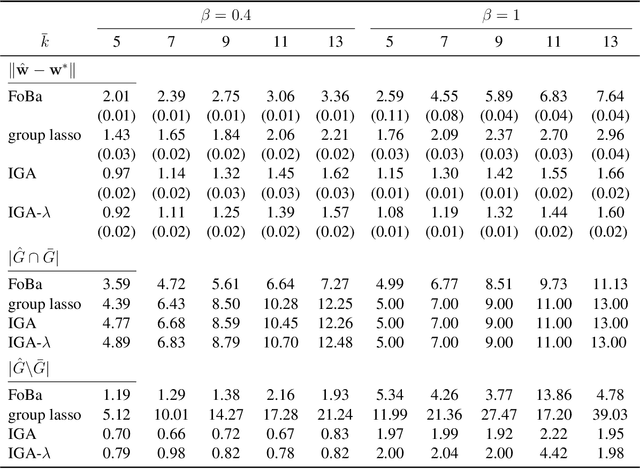
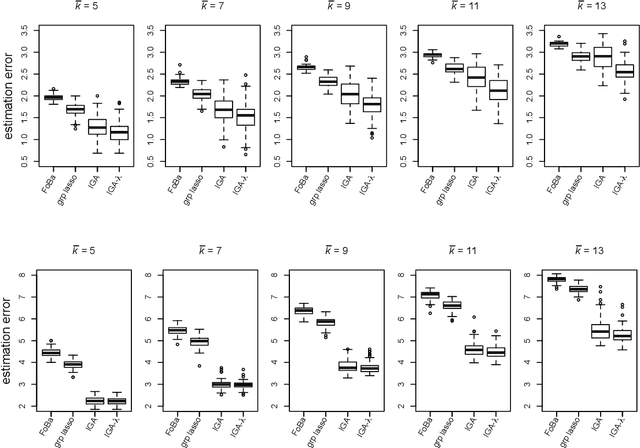
Sparsity learning with known grouping structure has received considerable attention due to wide modern applications in high-dimensional data analysis. Although advantages of using group information have been well-studied by shrinkage-based approaches, benefits of group sparsity have not been well-documented for greedy-type methods, which much limits our understanding and use of this important class of methods. In this paper, generalizing from a popular forward-backward greedy approach, we propose a new interactive greedy algorithm for group sparsity learning and prove that the proposed greedy-type algorithm attains the desired benefits of group sparsity under high dimensional settings. An estimation error bound refining other existing methods and a guarantee for group support recovery are also established simultaneously. In addition, we incorporate a general M-estimation framework and introduce an interactive feature to allow extra algorithm flexibility without compromise in theoretical properties. The promising use of our proposal is demonstrated through numerical evaluations including a real industrial application in human activity recognition at home. Supplementary materials for this article are available online.

Distributed Bayesian Piecewise Sparse Linear Models

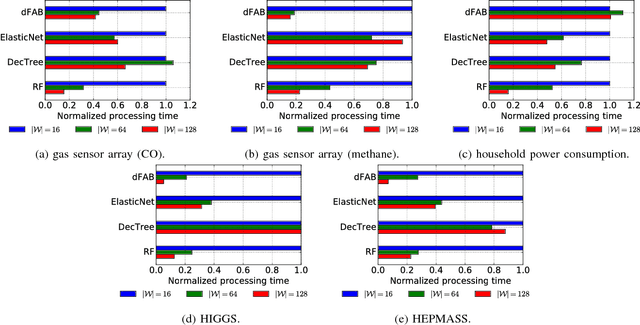
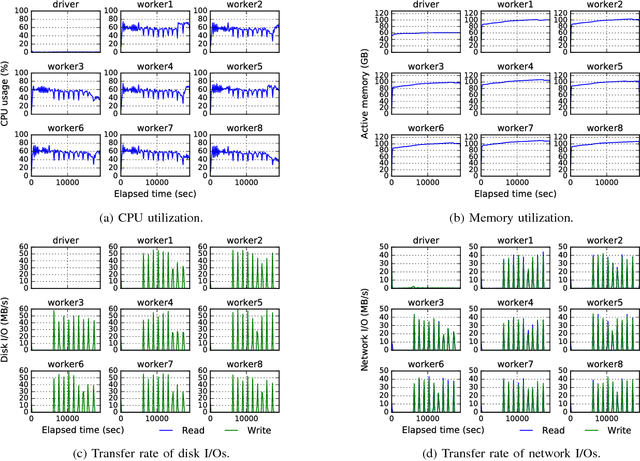
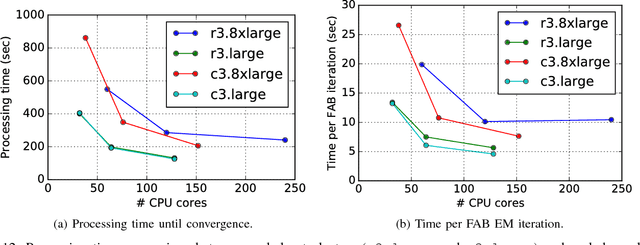
The importance of interpretability of machine learning models has been increasing due to emerging enterprise predictive analytics, threat of data privacy, accountability of artificial intelligence in society, and so on. Piecewise linear models have been actively studied to achieve both accuracy and interpretability. They often produce competitive accuracy against state-of-the-art non-linear methods. In addition, their representations (i.e., rule-based segmentation plus sparse linear formula) are often preferred by domain experts. A disadvantage of such models, however, is high computational cost for simultaneous determinations of the number of "pieces" and cardinality of each linear predictor, which has restricted their applicability to middle-scale data sets. This paper proposes a distributed factorized asymptotic Bayesian (FAB) inference of learning piece-wise sparse linear models on distributed memory architectures. The distributed FAB inference solves the simultaneous model selection issue without communicating $O(N)$ data where N is the number of training samples and achieves linear scale-out against the number of CPU cores. Experimental results demonstrate that the distributed FAB inference achieves high prediction accuracy and performance scalability with both synthetic and benchmark data.

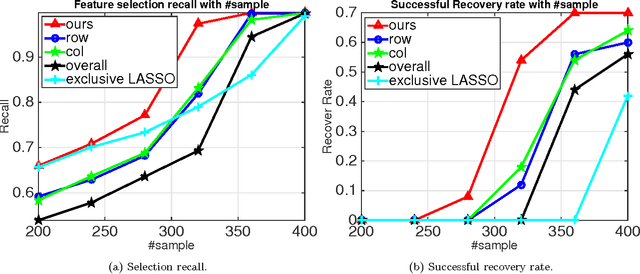
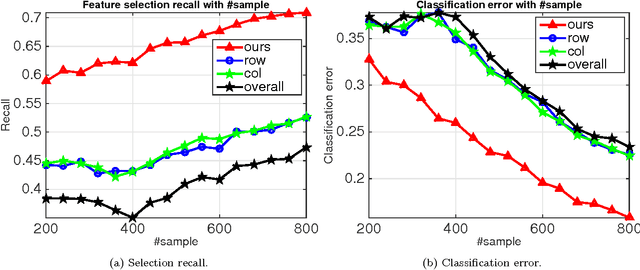
On The Projection Operator to A Three-view Cardinality Constrained Set

The cardinality constraint is an intrinsic way to restrict the solution structure in many domains, for example, sparse learning, feature selection, and compressed sensing. To solve a cardinality constrained problem, the key challenge is to solve the projection onto the cardinality constraint set, which is NP-hard in general when there exist multiple overlapped cardinality constraints. In this paper, we consider the scenario where the overlapped cardinality constraints satisfy a Three-view Cardinality Structure (TVCS), which reflects the natural restriction in many applications, such as identification of gene regulatory networks and task-worker assignment problem. We cast the projection into a linear programming, and show that for TVCS, the vertex solution of this linear programming is the solution for the original projection problem. We further prove that such solution can be found with the complexity proportional to the number of variables and constraints. We finally use synthetic experiments and two interesting applications in bioinformatics and crowdsourcing to validate the proposed TVCS model and method.

Optimization Beyond Prediction: Prescriptive Price Optimization

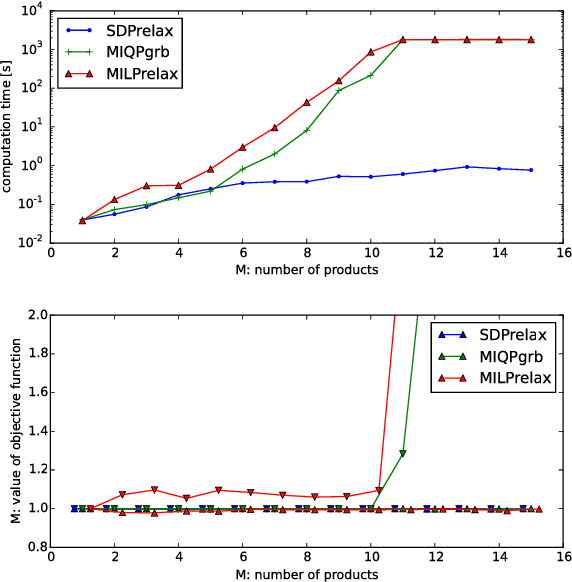
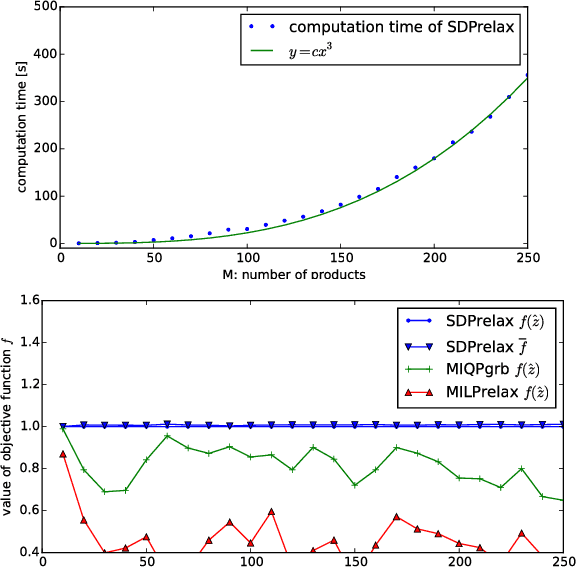
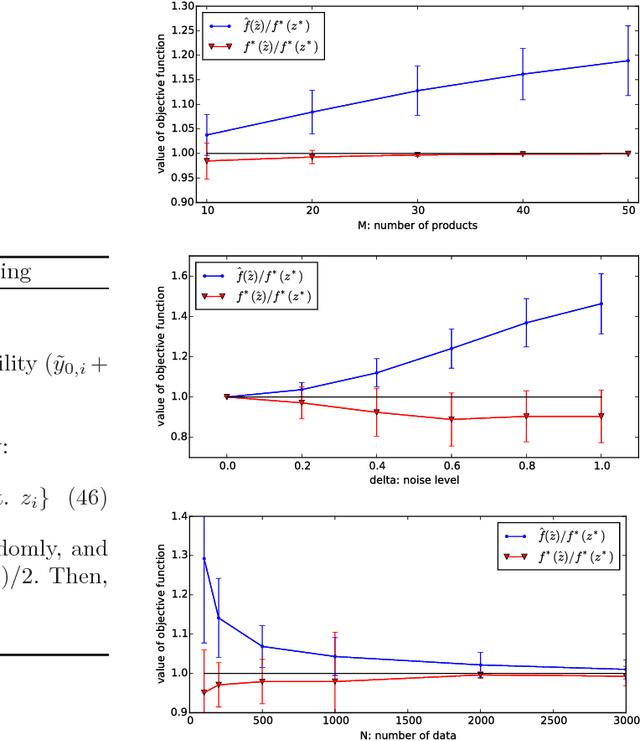
This paper addresses a novel data science problem, prescriptive price optimization, which derives the optimal price strategy to maximize future profit/revenue on the basis of massive predictive formulas produced by machine learning. The prescriptive price optimization first builds sales forecast formulas of multiple products, on the basis of historical data, which reveal complex relationships between sales and prices, such as price elasticity of demand and cannibalization. Then, it constructs a mathematical optimization problem on the basis of those predictive formulas. We present that the optimization problem can be formulated as an instance of binary quadratic programming (BQP). Although BQP problems are NP-hard in general and computationally intractable, we propose a fast approximation algorithm using a semi-definite programming (SDP) relaxation, which is closely related to the Goemans-Williamson's Max-Cut approximation. Our experiments on simulation and real retail datasets show that our prescriptive price optimization simultaneously derives the optimal prices of tens/hundreds products with practical computational time, that potentially improve 8.2% of gross profit of those products.

Factorized Asymptotic Bayesian Inference for Factorial Hidden Markov Models

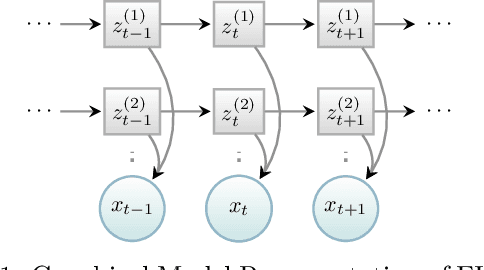
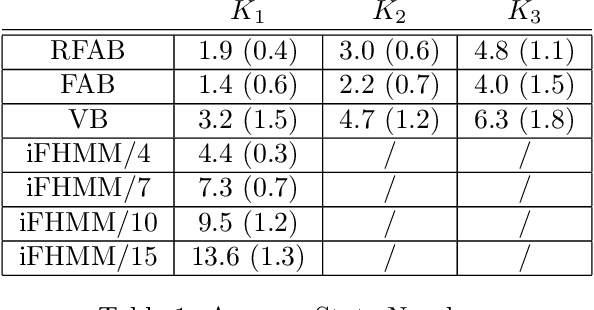
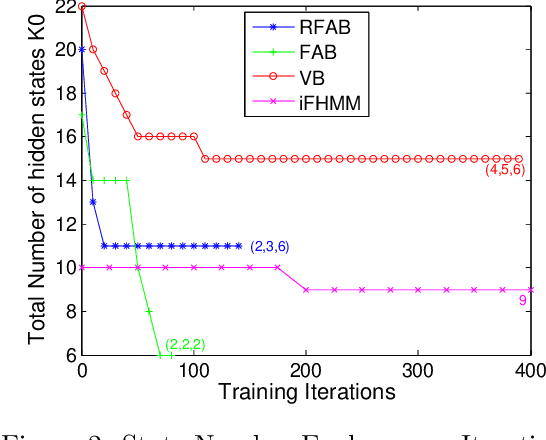
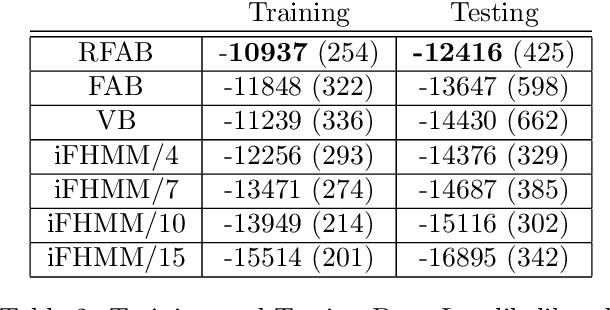
Factorial hidden Markov models (FHMMs) are powerful tools of modeling sequential data. Learning FHMMs yields a challenging simultaneous model selection issue, i.e., selecting the number of multiple Markov chains and the dimensionality of each chain. Our main contribution is to address this model selection issue by extending Factorized Asymptotic Bayesian (FAB) inference to FHMMs. First, we offer a better approximation of marginal log-likelihood than the previous FAB inference. Our key idea is to integrate out transition probabilities, yet still apply the Laplace approximation to emission probabilities. Second, we prove that if there are two very similar hidden states in an FHMM, i.e. one is redundant, then FAB will almost surely shrink and eliminate one of them, making the model parsimonious. Experimental results show that FAB for FHMMs significantly outperforms state-of-the-art nonparametric Bayesian iFHMM and Variational FHMM in model selection accuracy, with competitive held-out perplexity.

Rebuilding Factorized Information Criterion: Asymptotically Accurate Marginal Likelihood

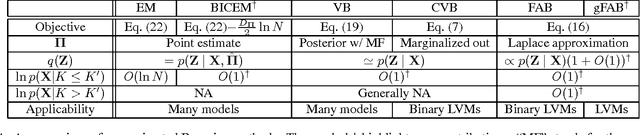
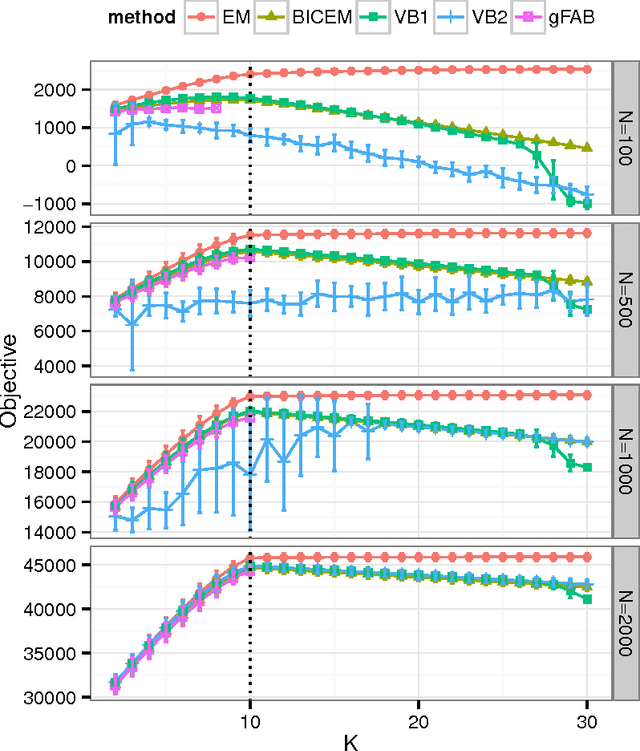
Factorized information criterion (FIC) is a recently developed approximation technique for the marginal log-likelihood, which provides an automatic model selection framework for a few latent variable models (LVMs) with tractable inference algorithms. This paper reconsiders FIC and fills theoretical gaps of previous FIC studies. First, we reveal the core idea of FIC that allows generalization for a broader class of LVMs, including continuous LVMs, in contrast to previous FICs, which are applicable only to binary LVMs. Second, we investigate the model selection mechanism of the generalized FIC. Our analysis provides a formal justification of FIC as a model selection criterion for LVMs and also a systematic procedure for pruning redundant latent variables that have been removed heuristically in previous studies. Third, we provide an interpretation of FIC as a variational free energy and uncover a few previously-unknown their relationships. A demonstrative study on Bayesian principal component analysis is provided and numerical experiments support our theoretical results.

Partition-wise Linear Models

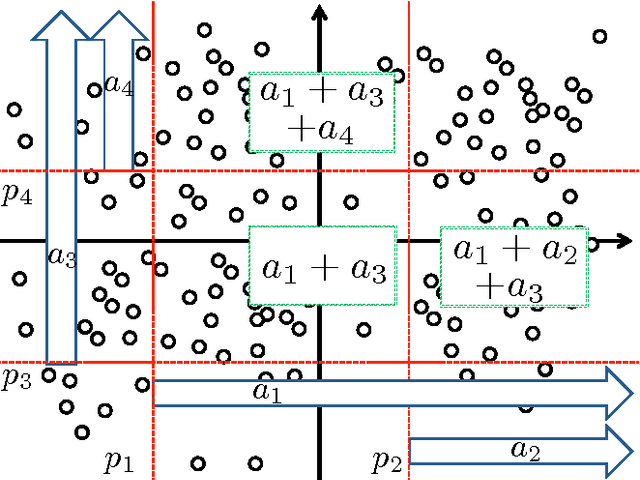
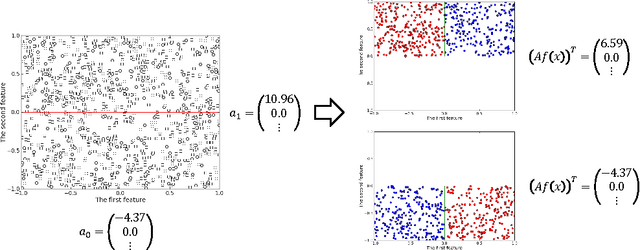
Region-specific linear models are widely used in practical applications because of their non-linear but highly interpretable model representations. One of the key challenges in their use is non-convexity in simultaneous optimization of regions and region-specific models. This paper proposes novel convex region-specific linear models, which we refer to as partition-wise linear models. Our key ideas are 1) assigning linear models not to regions but to partitions (region-specifiers) and representing region-specific linear models by linear combinations of partition-specific models, and 2) optimizing regions via partition selection from a large number of given partition candidates by means of convex structured regularizations. In addition to providing initialization-free globally-optimal solutions, our convex formulation makes it possible to derive a generalization bound and to use such advanced optimization techniques as proximal methods and decomposition of the proximal maps for sparsity-inducing regularizations. Experimental results demonstrate that our partition-wise linear models perform better than or are at least competitive with state-of-the-art region-specific or locally linear models.

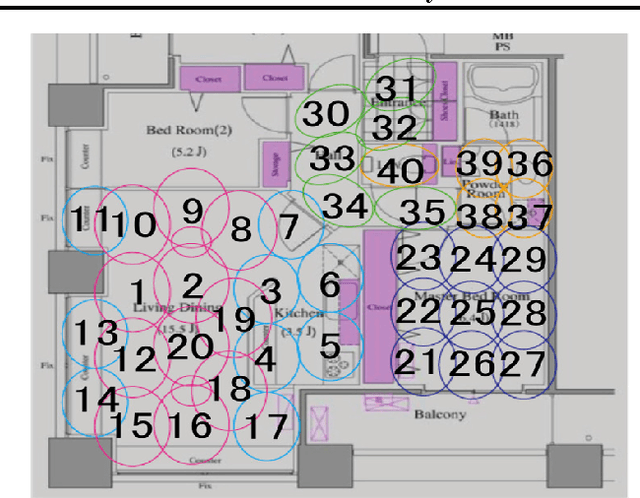
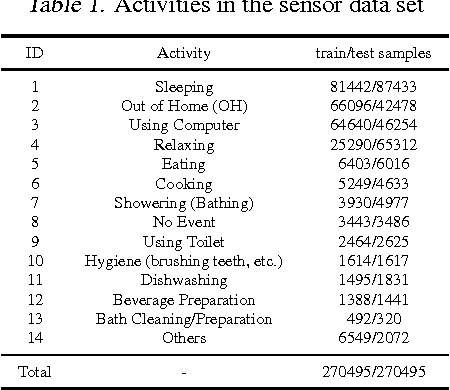
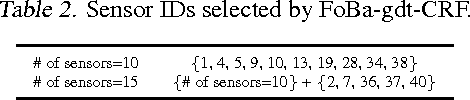
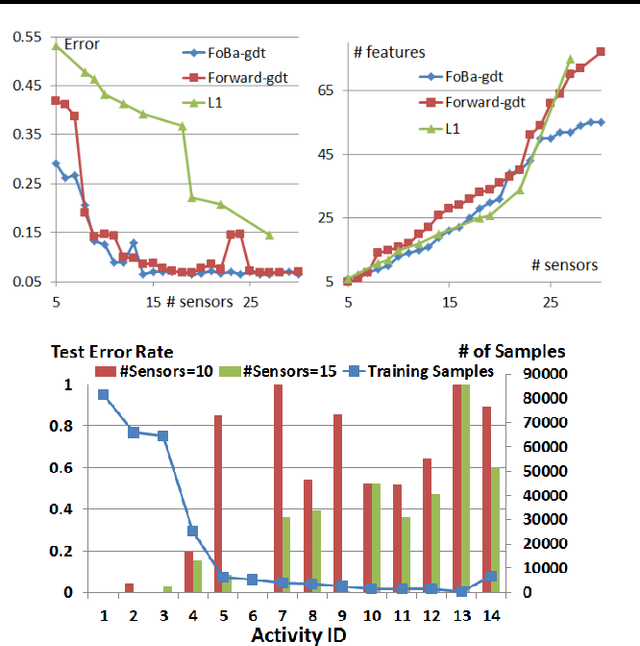
Forward-Backward Greedy Algorithms for General Convex Smooth Functions over A Cardinality Constraint

We consider forward-backward greedy algorithms for solving sparse feature selection problems with general convex smooth functions. A state-of-the-art greedy method, the Forward-Backward greedy algorithm (FoBa-obj) requires to solve a large number of optimization problems, thus it is not scalable for large-size problems. The FoBa-gdt algorithm, which uses the gradient information for feature selection at each forward iteration, significantly improves the efficiency of FoBa-obj. In this paper, we systematically analyze the theoretical properties of both forward-backward greedy algorithms. Our main contributions are: 1) We derive better theoretical bounds than existing analyses regarding FoBa-obj for general smooth convex functions; 2) We show that FoBa-gdt achieves the same theoretical performance as FoBa-obj under the same condition: restricted strong convexity condition. Our new bounds are consistent with the bounds of a special case (least squares) and fills a previously existing theoretical gap for general convex smooth functions; 3) We show that the restricted strong convexity condition is satisfied if the number of independent samples is more than $\bar{k}\log d$ where $\bar{k}$ is the sparsity number and $d$ is the dimension of the variable; 4) We apply FoBa-gdt (with the conditional random field objective) to the sensor selection problem for human indoor activity recognition and our results show that FoBa-gdt outperforms other methods (including the ones based on forward greedy selection and L1-regularization).

Factorized Asymptotic Bayesian Hidden Markov Models

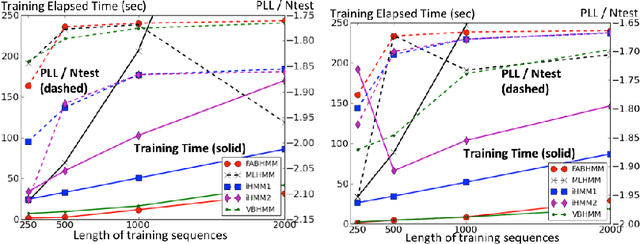
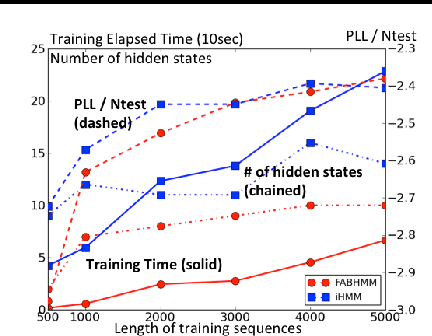
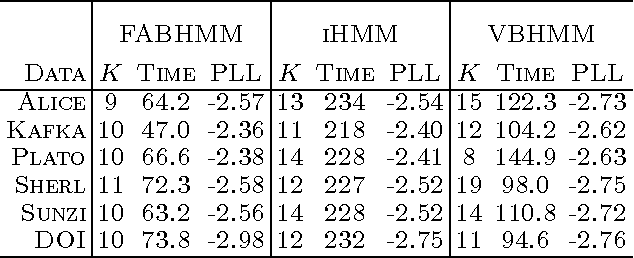
This paper addresses the issue of model selection for hidden Markov models (HMMs). We generalize factorized asymptotic Bayesian inference (FAB), which has been recently developed for model selection on independent hidden variables (i.e., mixture models), for time-dependent hidden variables. As with FAB in mixture models, FAB for HMMs is derived as an iterative lower bound maximization algorithm of a factorized information criterion (FIC). It inherits, from FAB for mixture models, several desirable properties for learning HMMs, such as asymptotic consistency of FIC with marginal log-likelihood, a shrinkage effect for hidden state selection, monotonic increase of the lower FIC bound through the iterative optimization. Further, it does not have a tunable hyper-parameter, and thus its model selection process can be fully automated. Experimental results shows that FAB outperforms states-of-the-art variational Bayesian HMM and non-parametric Bayesian HMM in terms of model selection accuracy and computational efficiency.