Understanding Diversity based Pruning of Neural Networks -- Statistical Mechanical Analysis

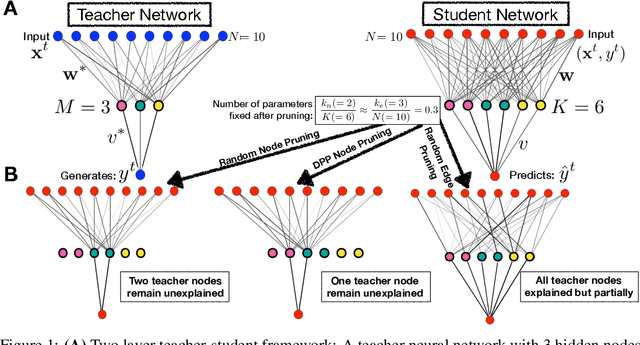
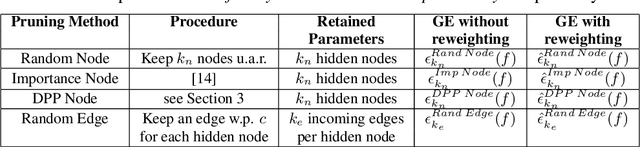
Deep learning architectures with a huge number of parameters are often compressed using pruning techniques to ensure computational efficiency of inference during deployment. Despite multitude of empirical advances, there is no theoretical understanding of the effectiveness of different pruning methods. We address this issue by setting up the problem in the statistical mechanics formulation of a teacher-student framework and deriving generalization error (GE) bounds of specific pruning methods. This theoretical premise allows comparison between pruning methods and we use it to investigate compression of neural networks via diversity-based pruning methods. A recent work showed that Determinantal Point Process (DPP) based node pruning method is notably superior to competing approaches when tested on real datasets. Using GE bounds in the aforementioned setup we provide theoretical guarantees for their empirical observations. Another consistent finding in literature is that sparse neural networks (edge pruned) generalize better than dense neural networks (node pruned) for a fixed number of parameters. We use our theoretical setup to prove that baseline random edge pruning method performs better than DPP node pruning method. Finally, we draw motivation from our theoretical results to propose a DPP edge pruning technique for neural networks which empirically outperforms other competing pruning methods on real datasets.

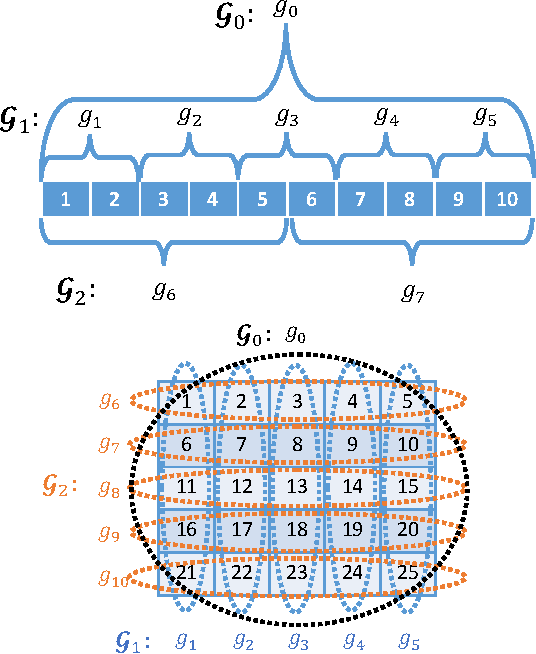
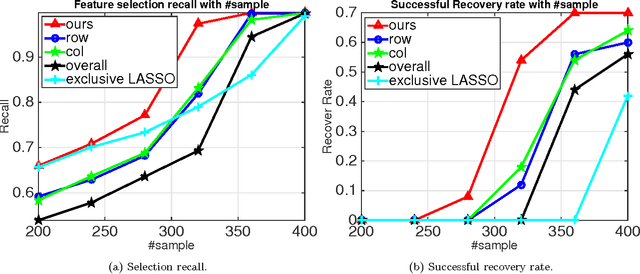
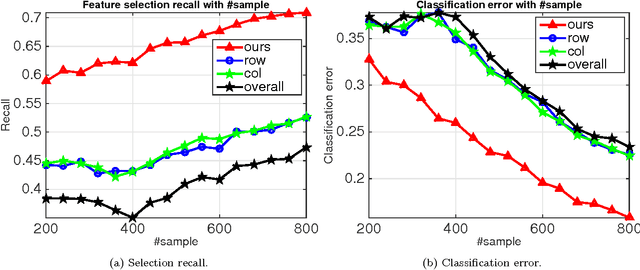
On The Projection Operator to A Three-view Cardinality Constrained Set

The cardinality constraint is an intrinsic way to restrict the solution structure in many domains, for example, sparse learning, feature selection, and compressed sensing. To solve a cardinality constrained problem, the key challenge is to solve the projection onto the cardinality constraint set, which is NP-hard in general when there exist multiple overlapped cardinality constraints. In this paper, we consider the scenario where the overlapped cardinality constraints satisfy a Three-view Cardinality Structure (TVCS), which reflects the natural restriction in many applications, such as identification of gene regulatory networks and task-worker assignment problem. We cast the projection into a linear programming, and show that for TVCS, the vertex solution of this linear programming is the solution for the original projection problem. We further prove that such solution can be found with the complexity proportional to the number of variables and constraints. We finally use synthetic experiments and two interesting applications in bioinformatics and crowdsourcing to validate the proposed TVCS model and method.

Rapid Mixing Swendsen-Wang Sampler for Stochastic Partitioned Attractive Models

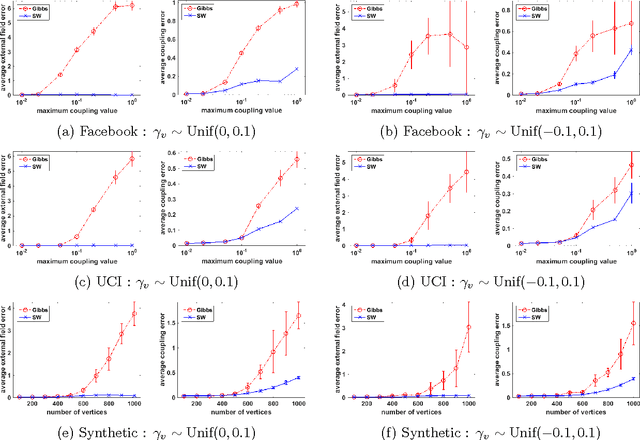
The Gibbs sampler is a particularly popular Markov chain used for learning and inference problems in Graphical Models (GMs). These tasks are computationally intractable in general, and the Gibbs sampler often suffers from slow mixing. In this paper, we study the Swendsen-Wang dynamics which is a more sophisticated Markov chain designed to overcome bottlenecks that impede the Gibbs sampler. We prove O(\log n) mixing time for attractive binary pairwise GMs (i.e., ferromagnetic Ising models) on stochastic partitioned graphs having n vertices, under some mild conditions, including low temperature regions where the Gibbs sampler provably mixes exponentially slow. Our experiments also confirm that the Swendsen-Wang sampler significantly outperforms the Gibbs sampler when they are used for learning parameters of attractive GMs.

Subset Selection for Gaussian Markov Random Fields

Given a Gaussian Markov random field, we consider the problem of selecting a subset of variables to observe which minimizes the total expected squared prediction error of the unobserved variables. We first show that finding an exact solution is NP-hard even for a restricted class of Gaussian Markov random fields, called Gaussian free fields, which arise in semi-supervised learning and computer vision. We then give a simple greedy approximation algorithm for Gaussian free fields on arbitrary graphs. Finally, we give a message passing algorithm for general Gaussian Markov random fields on bounded tree-width graphs.

Density estimation in linear time

We consider the problem of choosing a density estimate from a set of distributions F, minimizing the L1-distance to an unknown distribution (Devroye, Lugosi 2001). Devroye and Lugosi analyze two algorithms for the problem: Scheffe tournament winner and minimum distance estimate. The Scheffe tournament estimate requires fewer computations than the minimum distance estimate, but has strictly weaker guarantees than the latter. We focus on the computational aspect of density estimation. We present two algorithms, both with the same guarantee as the minimum distance estimate. The first one, a modification of the minimum distance estimate, uses the same number (quadratic in |F|) of computations as the Scheffe tournament. The second one, called ``efficient minimum loss-weight estimate,'' uses only a linear number of computations, assuming that F is preprocessed. We also give examples showing that the guarantees of the algorithms cannot be improved and explore randomized algorithms for density estimation.