One-Shot Learning for k-SAT

Consider a $k$-SAT formula $\Phi$ where every variable appears at most $d$ times, and let $\sigma$ be a satisfying assignment of $\Phi$ sampled proportionally to $e^{\beta m(\sigma)}$ where $m(\sigma)$ is the number of variables set to true and $\beta$ is a real parameter. Given $\Phi$ and $\sigma$, can we learn the value of $\beta$ efficiently? This problem falls into a recent line of works about single-sample ("one-shot") learning of Markov random fields. The $k$-SAT setting we consider here was recently studied by Galanis, Kandiros, and Kalavasis (SODA'24) where they showed that single-sample learning is possible when roughly $d\leq 2^{k/6.45}$ and impossible when $d\geq (k+1) 2^{k-1}$. Crucially, for their impossibility results they used the existence of unsatisfiable instances which, aside from the gap in $d$, left open the question of whether the feasibility threshold for one-shot learning is dictated by the satisfiability threshold of $k$-SAT formulas of bounded degree. Our main contribution is to answer this question negatively. We show that one-shot learning for $k$-SAT is infeasible well below the satisfiability threshold; in fact, we obtain impossibility results for degrees $d$ as low as $k^2$ when $\beta$ is sufficiently large, and bootstrap this to small values of $\beta$ when $d$ scales exponentially with $k$, via a probabilistic construction. On the positive side, we simplify the analysis of the learning algorithm and obtain significantly stronger bounds on $d$ in terms of $\beta$. In particular, for the uniform case $\beta\rightarrow 0$ that has been studied extensively in the sampling literature, our analysis shows that learning is possible under the condition $d\lesssim 2^{k/2}$. This is nearly optimal (up to constant factors) in the sense that it is known that sampling a uniformly-distributed satisfying assignment is NP-hard for $d\gtrsim 2^{k/2}$.

Learning Hard-Constrained Models with One Sample

We consider the problem of estimating the parameters of a Markov Random Field with hard-constraints using a single sample. As our main running examples, we use the $k$-SAT and the proper coloring models, as well as general $H$-coloring models; for all of these we obtain both positive and negative results. In contrast to the soft-constrained case, we show in particular that single-sample estimation is not always possible, and that the existence of an estimator is related to the existence of non-satisfiable instances. Our algorithms are based on the pseudo-likelihood estimator. We show variance bounds for this estimator using coupling techniques inspired, in the case of $k$-SAT, by Moitra's sampling algorithm (JACM, 2019); our positive results for colorings build on this new coupling approach. For $q$-colorings on graphs with maximum degree $d$, we give a linear-time estimator when $q>d+1$, whereas the problem is non-identifiable when $q\leq d+1$. For general $H$-colorings, we show that standard conditions that guarantee sampling, such as Dobrushin's condition, are insufficient for one-sample learning; on the positive side, we provide a general condition that is sufficient to guarantee linear-time learning and obtain applications for proper colorings and permissive models. For the $k$-SAT model on formulas with maximum degree $d$, we provide a linear-time estimator when $k\gtrsim 6.45\log d$, whereas the problem becomes non-identifiable when $k\lesssim \log d$.

Rapid Mixing Swendsen-Wang Sampler for Stochastic Partitioned Attractive Models

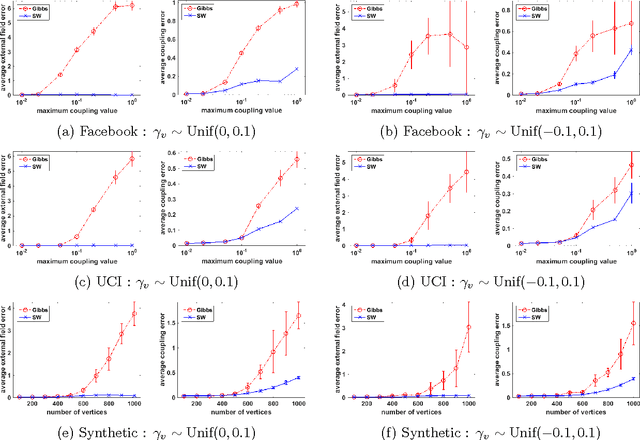
The Gibbs sampler is a particularly popular Markov chain used for learning and inference problems in Graphical Models (GMs). These tasks are computationally intractable in general, and the Gibbs sampler often suffers from slow mixing. In this paper, we study the Swendsen-Wang dynamics which is a more sophisticated Markov chain designed to overcome bottlenecks that impede the Gibbs sampler. We prove O(\log n) mixing time for attractive binary pairwise GMs (i.e., ferromagnetic Ising models) on stochastic partitioned graphs having n vertices, under some mild conditions, including low temperature regions where the Gibbs sampler provably mixes exponentially slow. Our experiments also confirm that the Swendsen-Wang sampler significantly outperforms the Gibbs sampler when they are used for learning parameters of attractive GMs.