Identity Testing for High-Dimensional Distributions via Entropy Tensorization

We present improved algorithms and matching statistical and computational lower bounds for the problem of identity testing $n$-dimensional distributions. In the identity testing problem, we are given as input an explicit distribution $\mu$, an $\varepsilon>0$, and access to a sampling oracle for a hidden distribution $\pi$. The goal is to distinguish whether the two distributions $\mu$ and $\pi$ are identical or are at least $\varepsilon$-far apart. When there is only access to full samples from the hidden distribution $\pi$, it is known that exponentially many samples may be needed, and hence previous works have studied identity testing with additional access to various conditional sampling oracles. We consider here a significantly weaker conditional sampling oracle, called the Coordinate Oracle, and provide a fairly complete computational and statistical characterization of the identity testing problem in this new model. We prove that if an analytic property known as approximate tensorization of entropy holds for the visible distribution $\mu$, then there is an efficient identity testing algorithm for any hidden $\pi$ that uses $\tilde{O}(n/\varepsilon)$ queries to the Coordinate Oracle. Approximate tensorization of entropy is a classical tool for proving optimal mixing time bounds of Markov chains for high-dimensional distributions, and recently has been established for many families of distributions via spectral independence. We complement our algorithmic result for identity testing with a matching $\Omega(n/\varepsilon)$ statistical lower bound for the number of queries under the Coordinate Oracle. We also prove a computational phase transition: for sparse antiferromagnetic Ising models over $\{+1,-1\}^n$, in the regime where approximate tensorization of entropy fails, there is no efficient identity testing algorithm unless RP=NP.

Hardness of Identity Testing for Restricted Boltzmann Machines and Potts models

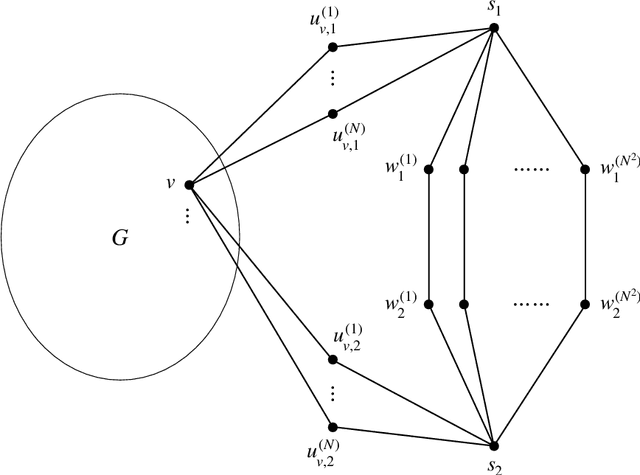
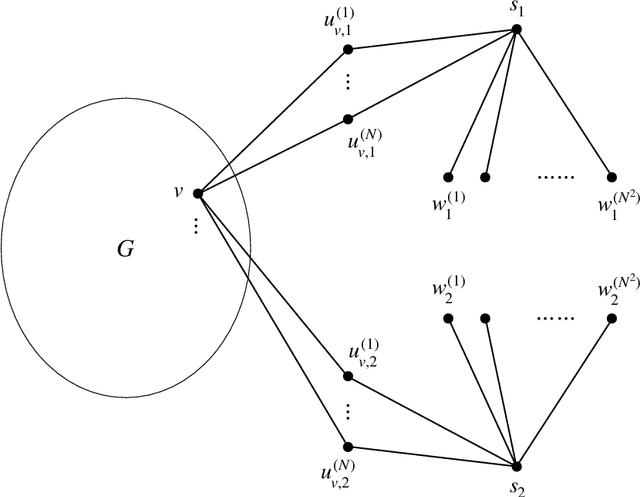
We study identity testing for restricted Boltzmann machines (RBMs), and more generally for undirected graphical models. Given sample access to the Gibbs distribution corresponding to an unknown or hidden model $M^*$ and given an explicit model $M$, can we distinguish if either $M = M^*$ or if they are (statistically) far apart? Daskalakis et al. (2018) presented a polynomial-time algorithm for identity testing for the ferromagnetic (attractive) Ising model. In contrast, for the antiferromagnetic (repulsive) Ising model, Bez\'akov\'a et al. (2019) proved that unless $RP=NP$ there is no identity testing algorithm when $\beta d=\omega(\log{n})$, where $d$ is the maximum degree of the visible graph and $\beta$ is the largest edge weight in absolute value. We prove analogous hardness results for RBMs (i.e., mixed Ising models on bipartite graphs), even when there are no latent variables or an external field. Specifically, we show that if $RP \neq NP$, then when $\beta d=\omega(\log{n})$ there is no polynomial-time algorithm for identity testing for RBMs; when $\beta d =O(\log{n})$ there is an efficient identity testing algorithm that utilizes the structure learning algorithm of Klivans and Meka (2017). In addition, we prove similar lower bounds for purely ferromagnetic RBMs with inconsistent external fields, and for the ferromagnetic Potts model. Previous hardness results for identity testing of Bez\'akov\'a et al. (2019) utilized the hardness of finding the maximum cuts, which corresponds to the ground states of the antiferromagnetic Ising model. Since RBMs are on bipartite graphs such an approach is not feasible. We instead introduce a general methodology to reduce from the corresponding approximate counting problem and utilize the phase transition that is exhibited by RBMs and the mean-field Potts model.

Lower bounds for testing graphical models: colorings and antiferromagnetic Ising models

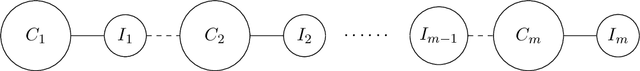
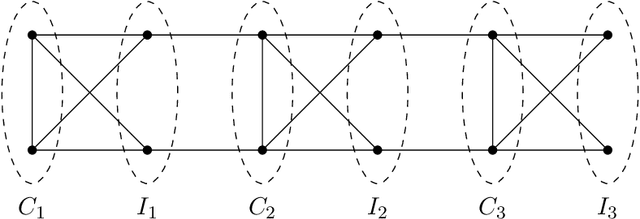
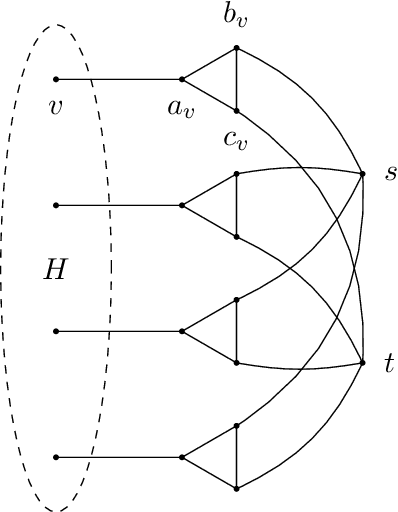
We study the identity testing problem in the context of spin systems or undirected graphical models, where it takes the following form: given the parameter specification of the model $M$ and a sampling oracle for the distribution $\mu_{\hat{M}}$ of an unknown model $\hat{M}$, can we efficiently determine if the two models $M$ and $\hat{M}$ are the same? We consider identity testing for both soft-constraint and hard-constraint systems. In particular, we prove hardness results in two prototypical cases, the Ising model and proper colorings, and explore whether identity testing is any easier than structure learning. For the ferromagnetic (attractive) Ising model, Daskalasis et al. (2018) presented a polynomial time algorithm for identity testing. We prove hardness results in the antiferromagnetic (repulsive) setting in the same regime of parameters where structure learning is known to require a super-polynomial number of samples. In particular, for $n$-vertex graphs of maximum degree $d$, we prove that if $|\beta| d = \omega(\log{n})$ (where $\beta$ is the inverse temperature parameter), then there is no polynomial running time identity testing algorithm unless $RP=NP$. We also establish computational lower bounds for a broader set of parameters under the (randomized) exponential time hypothesis. Our proofs utilize insights into the design of gadgets using random graphs in recent works concerning the hardness of approximate counting by Sly (2010). In the hard-constraint setting, we present hardness results for identity testing for proper colorings. Our results are based on the presumed hardness of #BIS, the problem of (approximately) counting independent sets in bipartite graphs. In particular, we prove that identity testing is hard in the same range of parameters where structure learning is known to be hard.

Structure Learning of $H$-colorings

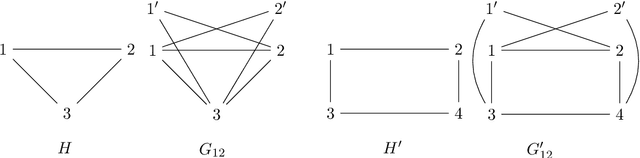
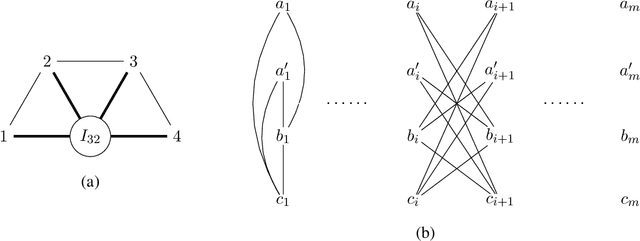
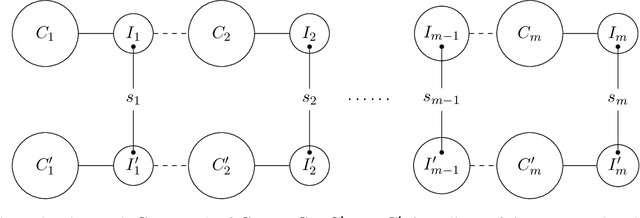
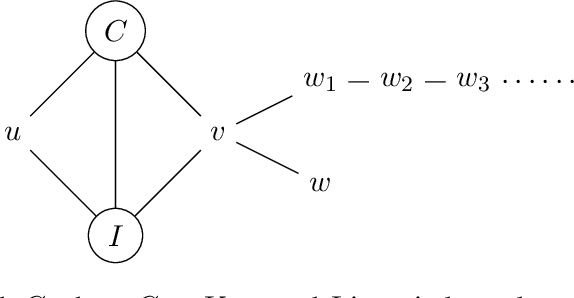
We study the structure learning problem for $H$-colorings, an important class of Markov random fields that capture key combinatorial structures on graphs, including proper colorings and independent sets, as well as spin systems from statistical physics. The learning problem is as follows: for a fixed (and known) constraint graph $H$ with $q$ colors and an unknown graph $G=(V,E)$ with $n$ vertices, given uniformly random $H$-colorings of $G$, how many samples are required to learn the edges of the unknown graph $G$? We give a characterization of $H$ for which the problem is identifiable for every $G$, i.e., we can learn $G$ with an infinite number of samples. We also show that there are identifiable constraint graphs for which one cannot hope to learn every graph $G$ efficiently. We focus particular attention on the case of proper vertex $q$-colorings of graphs of maximum degree $d$ where intriguing connections to statistical physics phase transitions appear. We prove that in the tree uniqueness region (when $q>d$) the problem is identifiable and we can learn $G$ in ${\rm poly}(d,q) \times O(n^2\log{n})$ time. In contrast for soft-constraint systems, such as the Ising model, the best possible running time is exponential in $d$. In the tree non-uniqueness region (when $q\leq d$) we prove that the problem is not identifiable and thus $G$ cannot be learned. Moreover, when $q<d-\sqrt{d} + \Theta(1)$ we prove that even learning an equivalent graph (any graph with the same set of $H$-colorings) is computationally hard---sample complexity is exponential in $n$ in the worst case. We further explore the connection between the efficiency/hardness of the structure learning problem and the uniqueness/non-uniqueness phase transition for general $H$-colorings and prove that under the well-known Dobrushin uniqueness condition, we can learn $G$ in ${\rm poly}(d,q)\times O(n^2\log{n})$ time.

Rapid Mixing Swendsen-Wang Sampler for Stochastic Partitioned Attractive Models

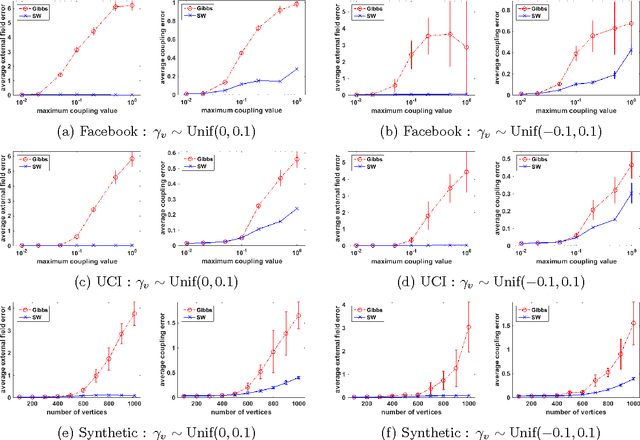
The Gibbs sampler is a particularly popular Markov chain used for learning and inference problems in Graphical Models (GMs). These tasks are computationally intractable in general, and the Gibbs sampler often suffers from slow mixing. In this paper, we study the Swendsen-Wang dynamics which is a more sophisticated Markov chain designed to overcome bottlenecks that impede the Gibbs sampler. We prove O(\log n) mixing time for attractive binary pairwise GMs (i.e., ferromagnetic Ising models) on stochastic partitioned graphs having n vertices, under some mild conditions, including low temperature regions where the Gibbs sampler provably mixes exponentially slow. Our experiments also confirm that the Swendsen-Wang sampler significantly outperforms the Gibbs sampler when they are used for learning parameters of attractive GMs.