Hardness of Identity Testing for Restricted Boltzmann Machines and Potts models
Paper and Code
Apr 22, 2020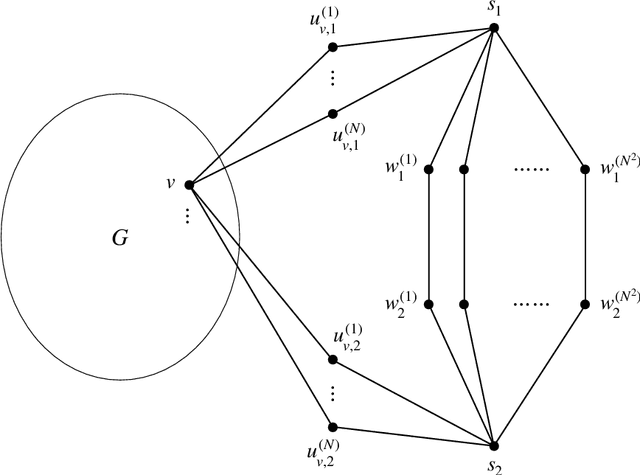
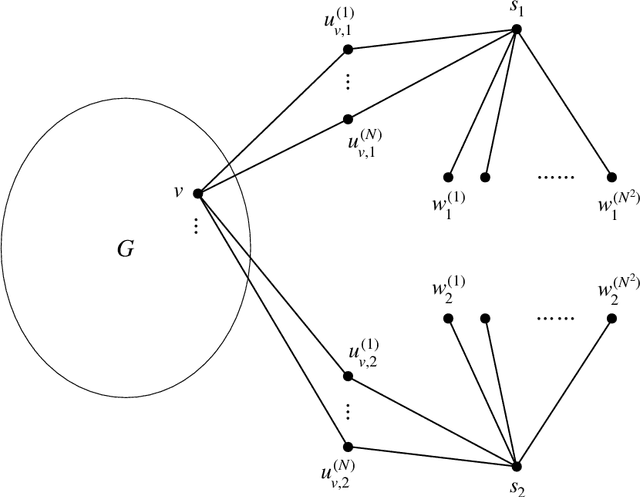
We study identity testing for restricted Boltzmann machines (RBMs), and more generally for undirected graphical models. Given sample access to the Gibbs distribution corresponding to an unknown or hidden model $M^*$ and given an explicit model $M$, can we distinguish if either $M = M^*$ or if they are (statistically) far apart? Daskalakis et al. (2018) presented a polynomial-time algorithm for identity testing for the ferromagnetic (attractive) Ising model. In contrast, for the antiferromagnetic (repulsive) Ising model, Bez\'akov\'a et al. (2019) proved that unless $RP=NP$ there is no identity testing algorithm when $\beta d=\omega(\log{n})$, where $d$ is the maximum degree of the visible graph and $\beta$ is the largest edge weight in absolute value. We prove analogous hardness results for RBMs (i.e., mixed Ising models on bipartite graphs), even when there are no latent variables or an external field. Specifically, we show that if $RP \neq NP$, then when $\beta d=\omega(\log{n})$ there is no polynomial-time algorithm for identity testing for RBMs; when $\beta d =O(\log{n})$ there is an efficient identity testing algorithm that utilizes the structure learning algorithm of Klivans and Meka (2017). In addition, we prove similar lower bounds for purely ferromagnetic RBMs with inconsistent external fields, and for the ferromagnetic Potts model. Previous hardness results for identity testing of Bez\'akov\'a et al. (2019) utilized the hardness of finding the maximum cuts, which corresponds to the ground states of the antiferromagnetic Ising model. Since RBMs are on bipartite graphs such an approach is not feasible. We instead introduce a general methodology to reduce from the corresponding approximate counting problem and utilize the phase transition that is exhibited by RBMs and the mean-field Potts model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge