Lower bounds for testing graphical models: colorings and antiferromagnetic Ising models

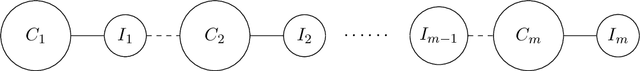
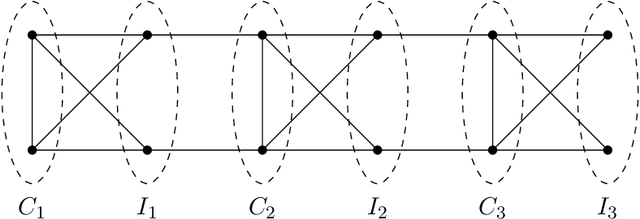
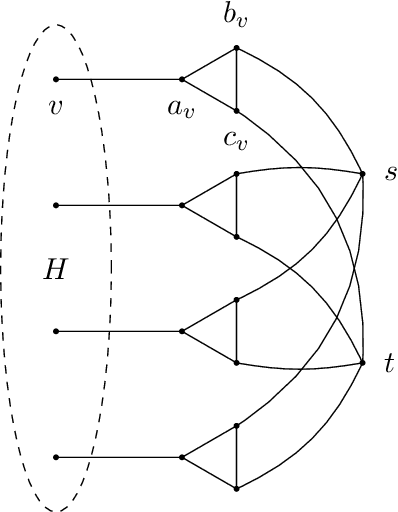
We study the identity testing problem in the context of spin systems or undirected graphical models, where it takes the following form: given the parameter specification of the model $M$ and a sampling oracle for the distribution $\mu_{\hat{M}}$ of an unknown model $\hat{M}$, can we efficiently determine if the two models $M$ and $\hat{M}$ are the same? We consider identity testing for both soft-constraint and hard-constraint systems. In particular, we prove hardness results in two prototypical cases, the Ising model and proper colorings, and explore whether identity testing is any easier than structure learning. For the ferromagnetic (attractive) Ising model, Daskalasis et al. (2018) presented a polynomial time algorithm for identity testing. We prove hardness results in the antiferromagnetic (repulsive) setting in the same regime of parameters where structure learning is known to require a super-polynomial number of samples. In particular, for $n$-vertex graphs of maximum degree $d$, we prove that if $|\beta| d = \omega(\log{n})$ (where $\beta$ is the inverse temperature parameter), then there is no polynomial running time identity testing algorithm unless $RP=NP$. We also establish computational lower bounds for a broader set of parameters under the (randomized) exponential time hypothesis. Our proofs utilize insights into the design of gadgets using random graphs in recent works concerning the hardness of approximate counting by Sly (2010). In the hard-constraint setting, we present hardness results for identity testing for proper colorings. Our results are based on the presumed hardness of #BIS, the problem of (approximately) counting independent sets in bipartite graphs. In particular, we prove that identity testing is hard in the same range of parameters where structure learning is known to be hard.