Rapid Mixing Swendsen-Wang Sampler for Stochastic Partitioned Attractive Models
Paper and Code
Apr 06, 2017
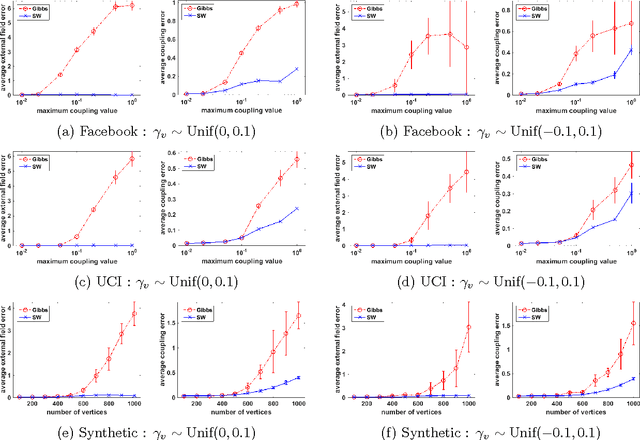
The Gibbs sampler is a particularly popular Markov chain used for learning and inference problems in Graphical Models (GMs). These tasks are computationally intractable in general, and the Gibbs sampler often suffers from slow mixing. In this paper, we study the Swendsen-Wang dynamics which is a more sophisticated Markov chain designed to overcome bottlenecks that impede the Gibbs sampler. We prove O(\log n) mixing time for attractive binary pairwise GMs (i.e., ferromagnetic Ising models) on stochastic partitioned graphs having n vertices, under some mild conditions, including low temperature regions where the Gibbs sampler provably mixes exponentially slow. Our experiments also confirm that the Swendsen-Wang sampler significantly outperforms the Gibbs sampler when they are used for learning parameters of attractive GMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge