Structure Learning of $H$-colorings
Paper and Code
Apr 24, 2018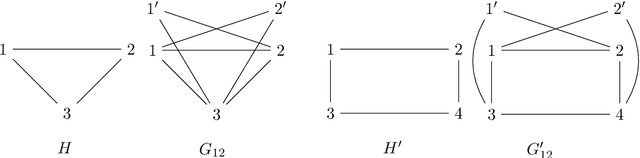
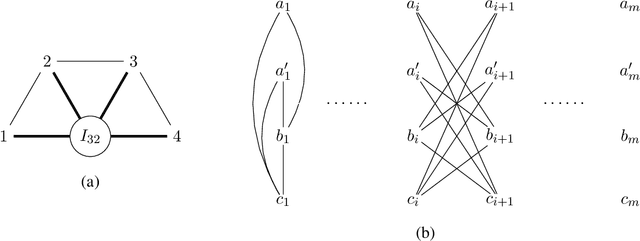
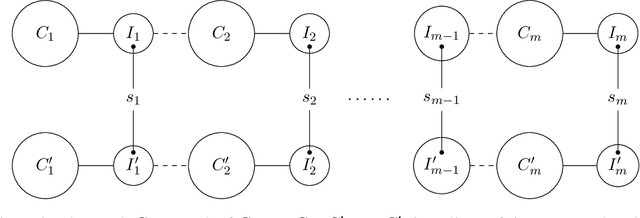
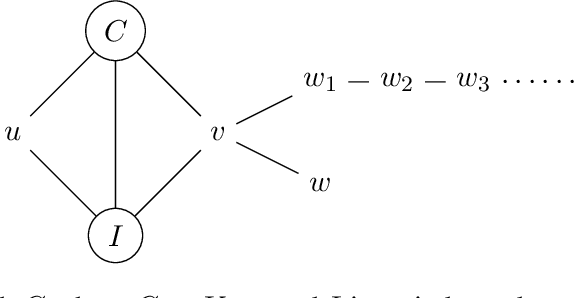
We study the structure learning problem for $H$-colorings, an important class of Markov random fields that capture key combinatorial structures on graphs, including proper colorings and independent sets, as well as spin systems from statistical physics. The learning problem is as follows: for a fixed (and known) constraint graph $H$ with $q$ colors and an unknown graph $G=(V,E)$ with $n$ vertices, given uniformly random $H$-colorings of $G$, how many samples are required to learn the edges of the unknown graph $G$? We give a characterization of $H$ for which the problem is identifiable for every $G$, i.e., we can learn $G$ with an infinite number of samples. We also show that there are identifiable constraint graphs for which one cannot hope to learn every graph $G$ efficiently. We focus particular attention on the case of proper vertex $q$-colorings of graphs of maximum degree $d$ where intriguing connections to statistical physics phase transitions appear. We prove that in the tree uniqueness region (when $q>d$) the problem is identifiable and we can learn $G$ in ${\rm poly}(d,q) \times O(n^2\log{n})$ time. In contrast for soft-constraint systems, such as the Ising model, the best possible running time is exponential in $d$. In the tree non-uniqueness region (when $q\leq d$) we prove that the problem is not identifiable and thus $G$ cannot be learned. Moreover, when $q<d-\sqrt{d} + \Theta(1)$ we prove that even learning an equivalent graph (any graph with the same set of $H$-colorings) is computationally hard---sample complexity is exponential in $n$ in the worst case. We further explore the connection between the efficiency/hardness of the structure learning problem and the uniqueness/non-uniqueness phase transition for general $H$-colorings and prove that under the well-known Dobrushin uniqueness condition, we can learn $G$ in ${\rm poly}(d,q)\times O(n^2\log{n})$ time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge