Understanding Diversity based Pruning of Neural Networks -- Statistical Mechanical Analysis
Paper and Code
Jun 30, 2020
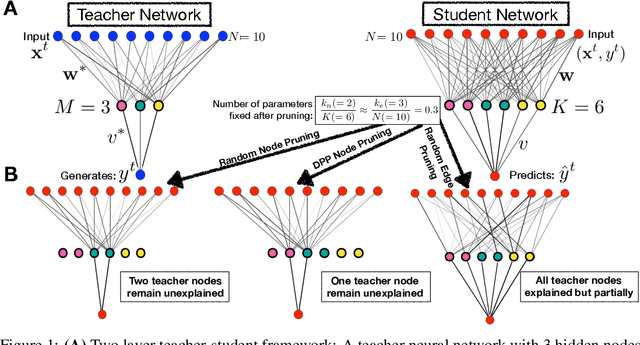
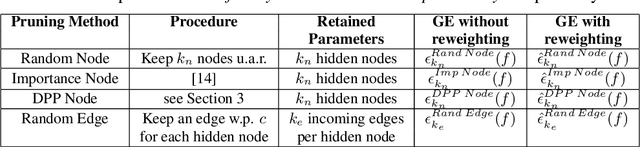

Deep learning architectures with a huge number of parameters are often compressed using pruning techniques to ensure computational efficiency of inference during deployment. Despite multitude of empirical advances, there is no theoretical understanding of the effectiveness of different pruning methods. We address this issue by setting up the problem in the statistical mechanics formulation of a teacher-student framework and deriving generalization error (GE) bounds of specific pruning methods. This theoretical premise allows comparison between pruning methods and we use it to investigate compression of neural networks via diversity-based pruning methods. A recent work showed that Determinantal Point Process (DPP) based node pruning method is notably superior to competing approaches when tested on real datasets. Using GE bounds in the aforementioned setup we provide theoretical guarantees for their empirical observations. Another consistent finding in literature is that sparse neural networks (edge pruned) generalize better than dense neural networks (node pruned) for a fixed number of parameters. We use our theoretical setup to prove that baseline random edge pruning method performs better than DPP node pruning method. Finally, we draw motivation from our theoretical results to propose a DPP edge pruning technique for neural networks which empirically outperforms other competing pruning methods on real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge