An Interactive Greedy Approach to Group Sparsity in High Dimensions
Paper and Code
Sep 26, 2018
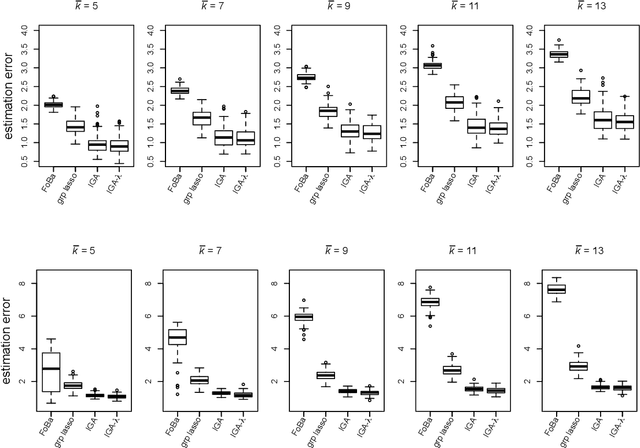
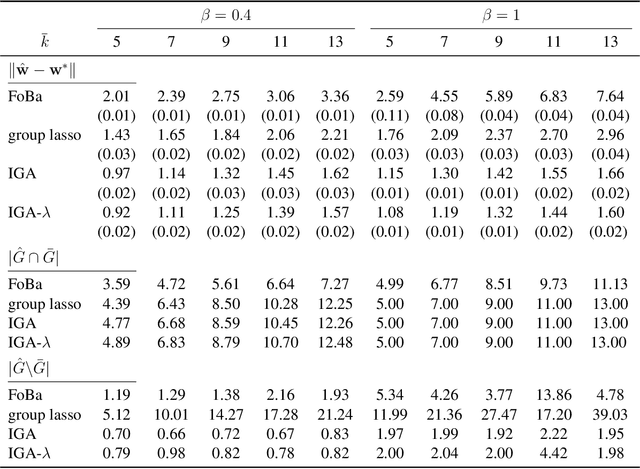
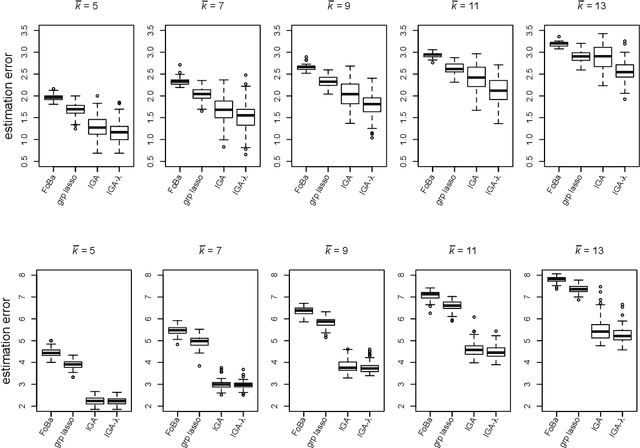
Sparsity learning with known grouping structure has received considerable attention due to wide modern applications in high-dimensional data analysis. Although advantages of using group information have been well-studied by shrinkage-based approaches, benefits of group sparsity have not been well-documented for greedy-type methods, which much limits our understanding and use of this important class of methods. In this paper, generalizing from a popular forward-backward greedy approach, we propose a new interactive greedy algorithm for group sparsity learning and prove that the proposed greedy-type algorithm attains the desired benefits of group sparsity under high dimensional settings. An estimation error bound refining other existing methods and a guarantee for group support recovery are also established simultaneously. In addition, we incorporate a general M-estimation framework and introduce an interactive feature to allow extra algorithm flexibility without compromise in theoretical properties. The promising use of our proposal is demonstrated through numerical evaluations including a real industrial application in human activity recognition at home. Supplementary materials for this article are available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge