A Framework for Model Search Across Multiple Machine Learning Implementations

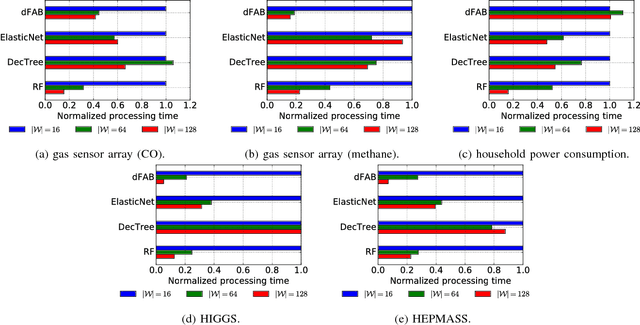
Several recently devised machine learning (ML) algorithms have shown improved accuracy for various predictive problems. Model searches, which explore to find an optimal ML algorithm and hyperparameter values for the target problem, play a critical role in such improvements. During a model search, data scientists typically use multiple ML implementations to construct several predictive models; however, it takes significant time and effort to employ multiple ML implementations due to the need to learn how to use them, prepare input data in several different formats, and compare their outputs. Our proposed framework addresses these issues by providing simple and unified coding method. It has been designed with the following two attractive features: i) new machine learning implementations can be added easily via common interfaces between the framework and ML implementations and ii) it can be scaled to handle large model configuration search spaces via profile-based scheduling. The results of our evaluation indicate that, with our framework, implementers need only write 55-144 lines of code to add a new ML implementation. They also show that ours was the fastest framework for the HIGGS dataset, and the second-fastest for the SECOM dataset.

Distributed Bayesian Piecewise Sparse Linear Models

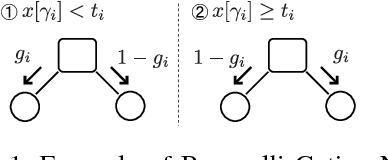
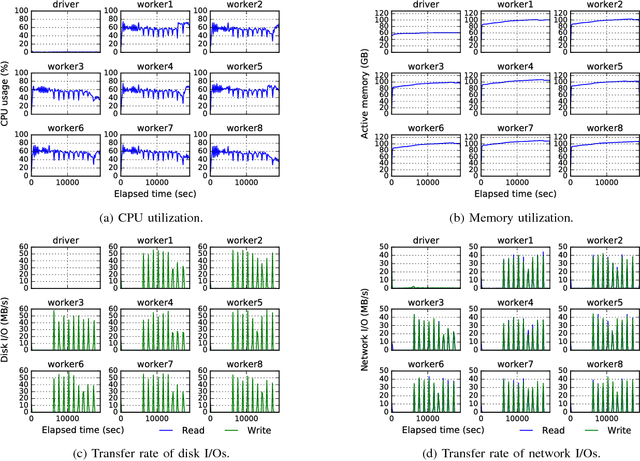
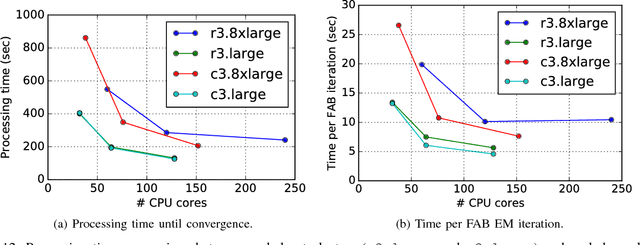
The importance of interpretability of machine learning models has been increasing due to emerging enterprise predictive analytics, threat of data privacy, accountability of artificial intelligence in society, and so on. Piecewise linear models have been actively studied to achieve both accuracy and interpretability. They often produce competitive accuracy against state-of-the-art non-linear methods. In addition, their representations (i.e., rule-based segmentation plus sparse linear formula) are often preferred by domain experts. A disadvantage of such models, however, is high computational cost for simultaneous determinations of the number of "pieces" and cardinality of each linear predictor, which has restricted their applicability to middle-scale data sets. This paper proposes a distributed factorized asymptotic Bayesian (FAB) inference of learning piece-wise sparse linear models on distributed memory architectures. The distributed FAB inference solves the simultaneous model selection issue without communicating $O(N)$ data where N is the number of training samples and achieves linear scale-out against the number of CPU cores. Experimental results demonstrate that the distributed FAB inference achieves high prediction accuracy and performance scalability with both synthetic and benchmark data.