StepFun-Prover Preview: Let's Think and Verify Step by Step

We present StepFun-Prover Preview, a large language model designed for formal theorem proving through tool-integrated reasoning. Using a reinforcement learning pipeline that incorporates tool-based interactions, StepFun-Prover can achieve strong performance in generating Lean 4 proofs with minimal sampling. Our approach enables the model to emulate human-like problem-solving strategies by iteratively refining proofs based on real-time environment feedback. On the miniF2F-test benchmark, StepFun-Prover achieves a pass@1 success rate of $70.0\%$. Beyond advancing benchmark performance, we introduce an end-to-end training framework for developing tool-integrated reasoning models, offering a promising direction for automated theorem proving and Math AI assistant.

Spherical Motion Dynamics of Deep Neural Networks with Batch Normalization and Weight Decay

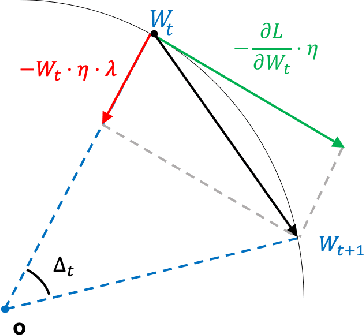
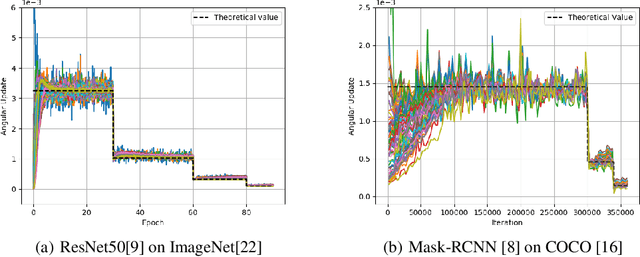
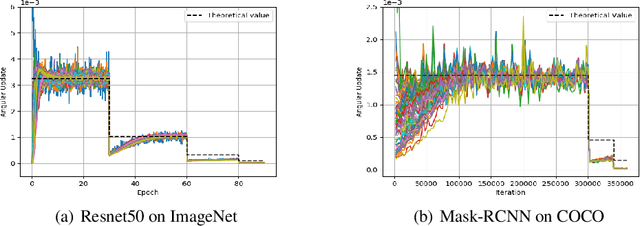
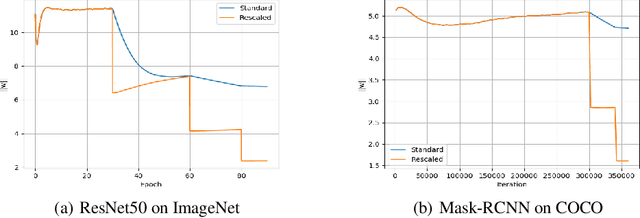
We comprehensively reveal the learning dynamics of deep neural networks (DNN) with batch normalization (BN) and weight decay (WD), named as Spherical Motion Dynamics (SMD). Our theorem on SMD is based on the scale-invariant property of weights caused by BN, and regularization effect of WD. SMD shows the optimization trajectory of weights is like a spherical motion; and a new indicator, angular update is proposed to measure the update efficiency of DNN with BN and WD. We rigorously prove that the angular update is only determined by pre-defined hyper-parameters (i.e. learning rate, WD parameter and momentum coefficient), and provide their quantitative relationship. Most importantly, the quantitative result of SMD can perfectly match the empirical observation in complex and large scale computer vision tasks like ImageNet and COCO with standard training schemes. SMD can also yield reasonable interpretations on some phenomena about BN from an entirely new perspective, including avoidance of vanishing and exploding gradient, no risk of being trapped into sharp minima, and sudden drop of loss when shrinking learning rate. Further, to present the practical significance of SMD, we discuss the connection between SMD and commonly used learning rate tuning scheme: Linear Scaling Principle.

Angle-based Search Space Shrinking for Neural Architecture Search

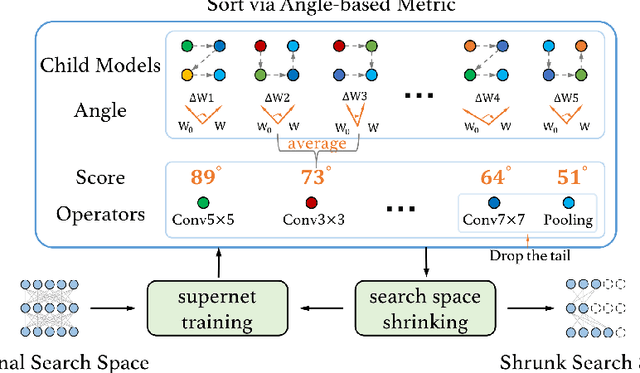
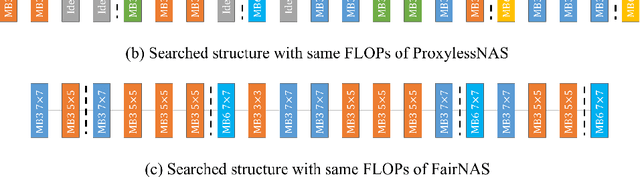
In this work, we present a simple and general search space shrinking method, called Angle-Based search space Shrinking (ABS), for Neural Architecture Search (NAS). Our approach progressively simplifies the original search space by dropping unpromising candidates, thus can reduce difficulties for existing NAS methods to find superior architectures. In particular, we propose an angle-based metric to guide the shrinking process. We provide comprehensive evidences showing that, in weight-sharing supernet, the proposed metric is more stable and accurate than accuracy-based and magnitude-based metrics to predict the capability of child models. We also show that the angle-based metric can converge fast while training supernet, enabling us to get promising shrunk search spaces efficiently. ABS can easily apply to most of popular NAS approaches (e.g. SPOS, FariNAS, ProxylessNAS, DARTS and PDARTS). Comprehensive experiments show that ABS can dramatically enhance existing NAS approaches by providing a promising shrunk search space.

Towards Stabilizing Batch Statistics in Backward Propagation of Batch Normalization

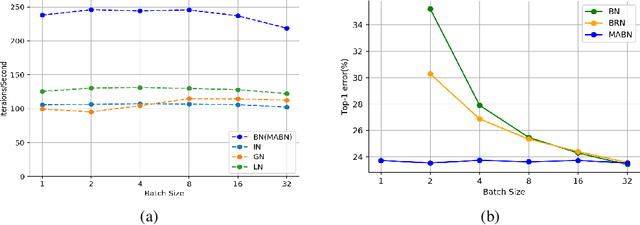
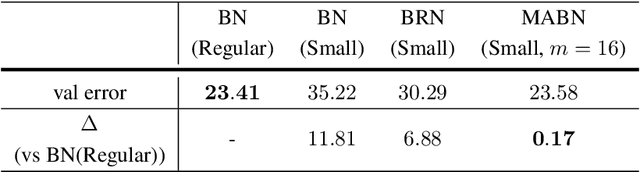
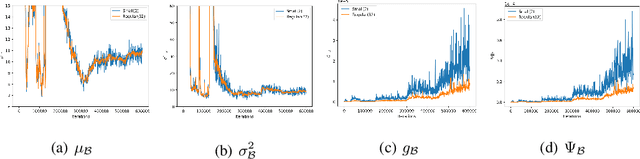
Batch Normalization (BN) is one of the most widely used techniques in Deep Learning field. But its performance can awfully degrade with insufficient batch size. This weakness limits the usage of BN on many computer vision tasks like detection or segmentation, where batch size is usually small due to the constraint of memory consumption. Therefore many modified normalization techniques have been proposed, which either fail to restore the performance of BN completely, or have to introduce additional nonlinear operations in inference procedure and increase huge consumption. In this paper, we reveal that there are two extra batch statistics involved in backward propagation of BN, on which has never been well discussed before. The extra batch statistics associated with gradients also can severely affect the training of deep neural network. Based on our analysis, we propose a novel normalization method, named Moving Average Batch Normalization (MABN). MABN can completely restore the performance of vanilla BN in small batch cases, without introducing any additional nonlinear operations in inference procedure. We prove the benefits of MABN by both theoretical analysis and experiments. Our experiments demonstrate the effectiveness of MABN in multiple computer vision tasks including ImageNet and COCO. The code has been released in https://github.com/megvii-model/MABN.

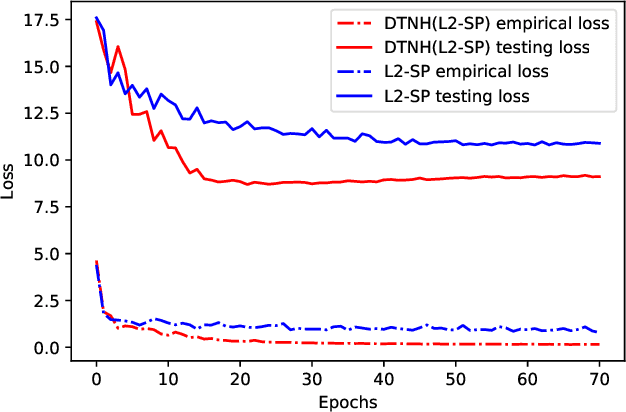
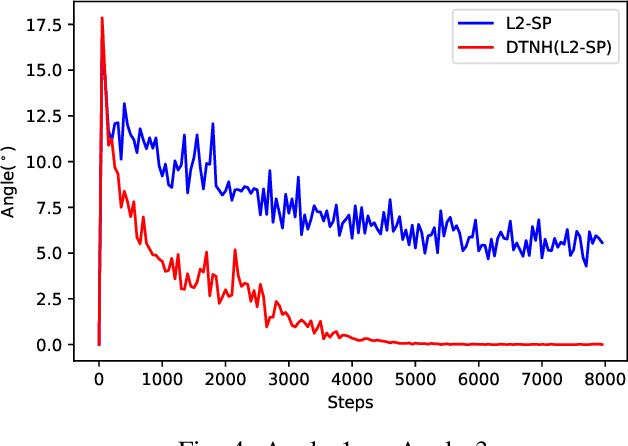
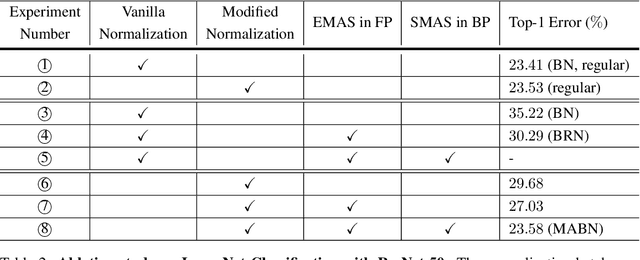
Towards Making Deep Transfer Learning Never Hurt

Transfer learning have been frequently used to improve deep neural network training through incorporating weights of pre-trained networks as the starting-point of optimization for regularization. While deep transfer learning can usually boost the performance with better accuracy and faster convergence, transferring weights from inappropriate networks hurts training procedure and may lead to even lower accuracy. In this paper, we consider deep transfer learning as minimizing a linear combination of empirical loss and regularizer based on pre-trained weights, where the regularizer would restrict the training procedure from lowering the empirical loss, with conflicted descent directions (e.g., derivatives). Following the view, we propose a novel strategy making regularization-based Deep Transfer learning Never Hurt (DTNH) that, for each iteration of training procedure, computes the derivatives of the two terms separately, then re-estimates a new descent direction that does not hurt the empirical loss minimization while preserving the regularization affects from the pre-trained weights. Extensive experiments have been done using common transfer learning regularizers, such as L2-SP and knowledge distillation, on top of a wide range of deep transfer learning benchmarks including Caltech, MIT indoor 67, CIFAR-10 and ImageNet. The empirical results show that the proposed descent direction estimation strategy DTNH can always improve the performance of deep transfer learning tasks based on all above regularizers, even when transferring pre-trained weights from inappropriate networks. All in all, DTNH strategy can improve state-of-the-art regularizers in all cases with 0.1%--7% higher accuracy in all experiments.

Neural Control Variates for Variance Reduction

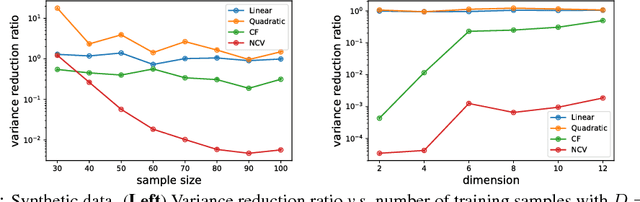
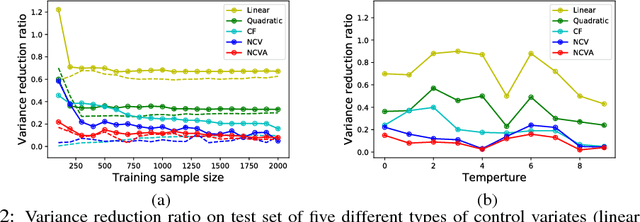
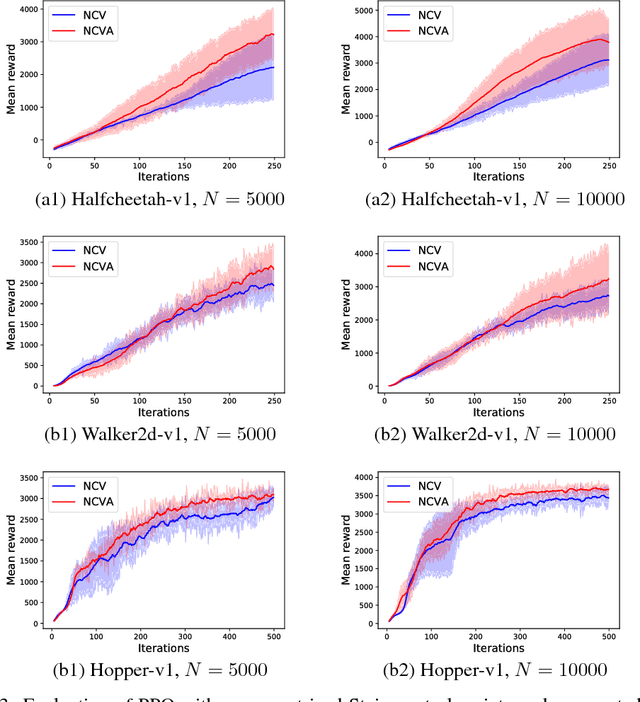
In statistics and machine learning, approximation of an intractable integration is often achieved by using the unbiased Monte Carlo estimator, but the variances of the estimation are generally high in many applications. Control variates approaches are well-known to reduce the variance of the estimation. These control variates are typically constructed by employing predefined parametric functions or polynomials, determined by using those samples drawn from the relevant distributions. Instead, we propose to construct those control variates by learning neural networks to handle the cases when test functions are complex. In many applications, obtaining a large number of samples for Monte Carlo estimation is expensive, which may result in overfitting when training a neural network. We thus further propose to employ auxiliary random variables induced by the original ones to extend data samples for training the neural networks. We apply the proposed control variates with augmented variables to thermodynamic integration and reinforcement learning. Experimental results demonstrate that our method can achieve significant variance reduction compared with other alternatives.