Spherical Motion Dynamics of Deep Neural Networks with Batch Normalization and Weight Decay
Paper and Code
Jul 02, 2020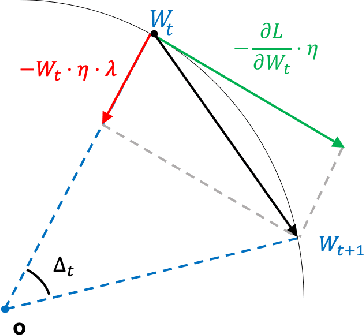
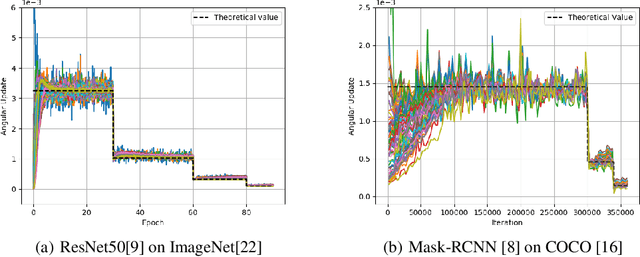
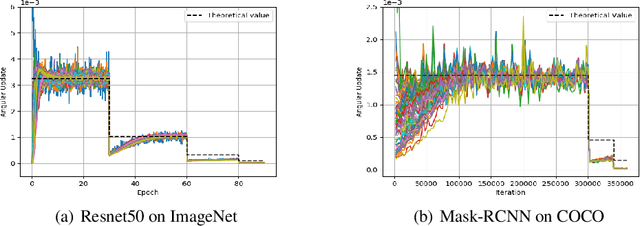
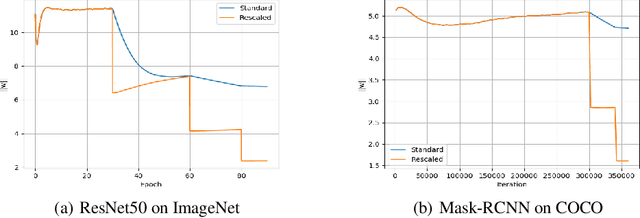
We comprehensively reveal the learning dynamics of deep neural networks (DNN) with batch normalization (BN) and weight decay (WD), named as Spherical Motion Dynamics (SMD). Our theorem on SMD is based on the scale-invariant property of weights caused by BN, and regularization effect of WD. SMD shows the optimization trajectory of weights is like a spherical motion; and a new indicator, angular update is proposed to measure the update efficiency of DNN with BN and WD. We rigorously prove that the angular update is only determined by pre-defined hyper-parameters (i.e. learning rate, WD parameter and momentum coefficient), and provide their quantitative relationship. Most importantly, the quantitative result of SMD can perfectly match the empirical observation in complex and large scale computer vision tasks like ImageNet and COCO with standard training schemes. SMD can also yield reasonable interpretations on some phenomena about BN from an entirely new perspective, including avoidance of vanishing and exploding gradient, no risk of being trapped into sharp minima, and sudden drop of loss when shrinking learning rate. Further, to present the practical significance of SMD, we discuss the connection between SMD and commonly used learning rate tuning scheme: Linear Scaling Principle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge