Neural Control Variates for Variance Reduction
Paper and Code
Jun 01, 2018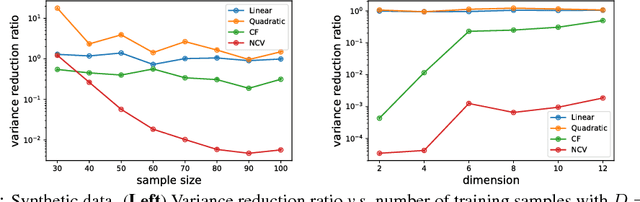
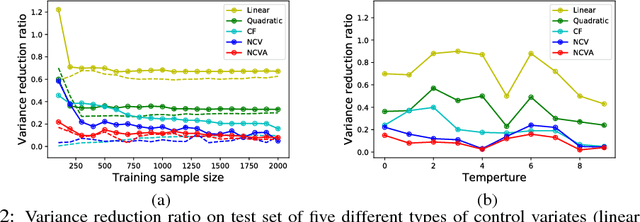
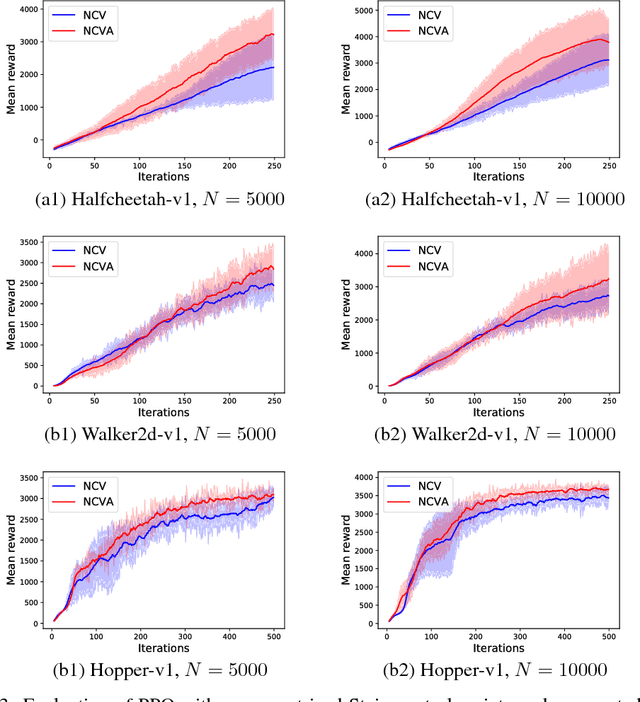
In statistics and machine learning, approximation of an intractable integration is often achieved by using the unbiased Monte Carlo estimator, but the variances of the estimation are generally high in many applications. Control variates approaches are well-known to reduce the variance of the estimation. These control variates are typically constructed by employing predefined parametric functions or polynomials, determined by using those samples drawn from the relevant distributions. Instead, we propose to construct those control variates by learning neural networks to handle the cases when test functions are complex. In many applications, obtaining a large number of samples for Monte Carlo estimation is expensive, which may result in overfitting when training a neural network. We thus further propose to employ auxiliary random variables induced by the original ones to extend data samples for training the neural networks. We apply the proposed control variates with augmented variables to thermodynamic integration and reinforcement learning. Experimental results demonstrate that our method can achieve significant variance reduction compared with other alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge