Beyond Standard MoE: Mixture of Latent Experts for Resource-Efficient Language Models

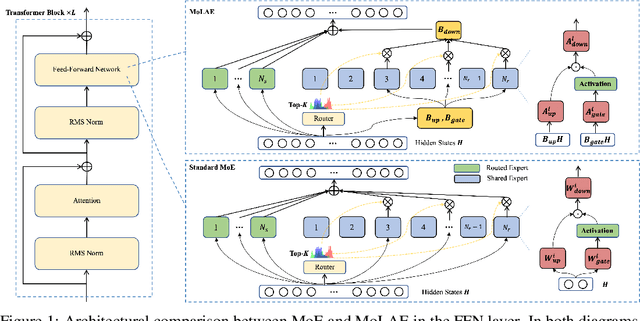
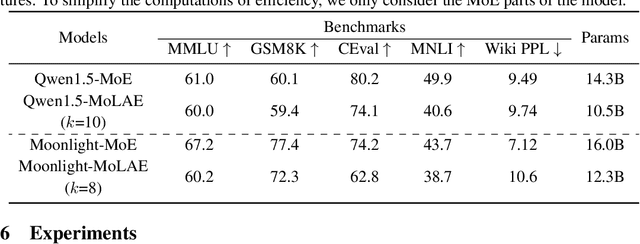
Mixture of Experts (MoE) has emerged as a pivotal architectural paradigm for efficient scaling of Large Language Models (LLMs), operating through selective activation of parameter subsets for each input token. Nevertheless, conventional MoE architectures encounter substantial challenges, including excessive memory utilization and communication overhead during training and inference, primarily attributable to the proliferation of expert modules. In this paper, we introduce Mixture of Latent Experts (MoLE), a novel parameterization methodology that facilitates the mapping of specific experts into a shared latent space. Specifically, all expert operations are systematically decomposed into two principal components: a shared projection into a lower-dimensional latent space, followed by expert-specific transformations with significantly reduced parametric complexity. This factorized approach substantially diminishes parameter count and computational requirements. Beyond the pretraining implementation of the MoLE architecture, we also establish a rigorous mathematical framework for transforming pre-trained MoE models into the MoLE architecture, characterizing the sufficient conditions for optimal factorization and developing a systematic two-phase algorithm for this conversion process. Our comprehensive theoretical analysis demonstrates that MoLE significantly enhances computational efficiency across multiple dimensions while preserving model representational capacity. Empirical evaluations corroborate our theoretical findings, confirming that MoLE achieves performance comparable to standard MoE implementations while substantially reducing resource requirements.

Automatic Operator-level Parallelism Planning for Distributed Deep Learning -- A Mixed-Integer Programming Approach

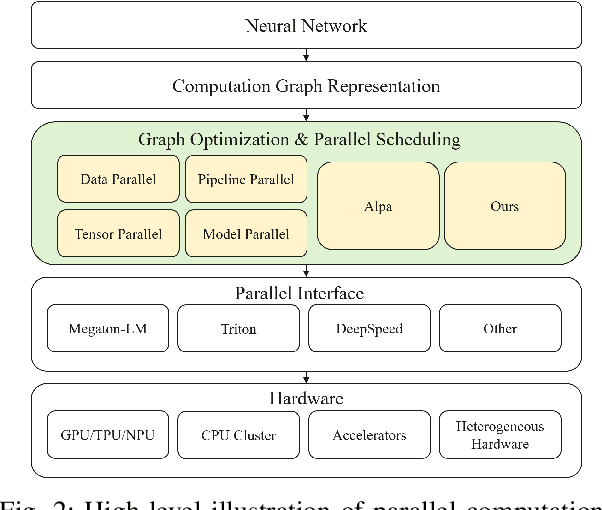
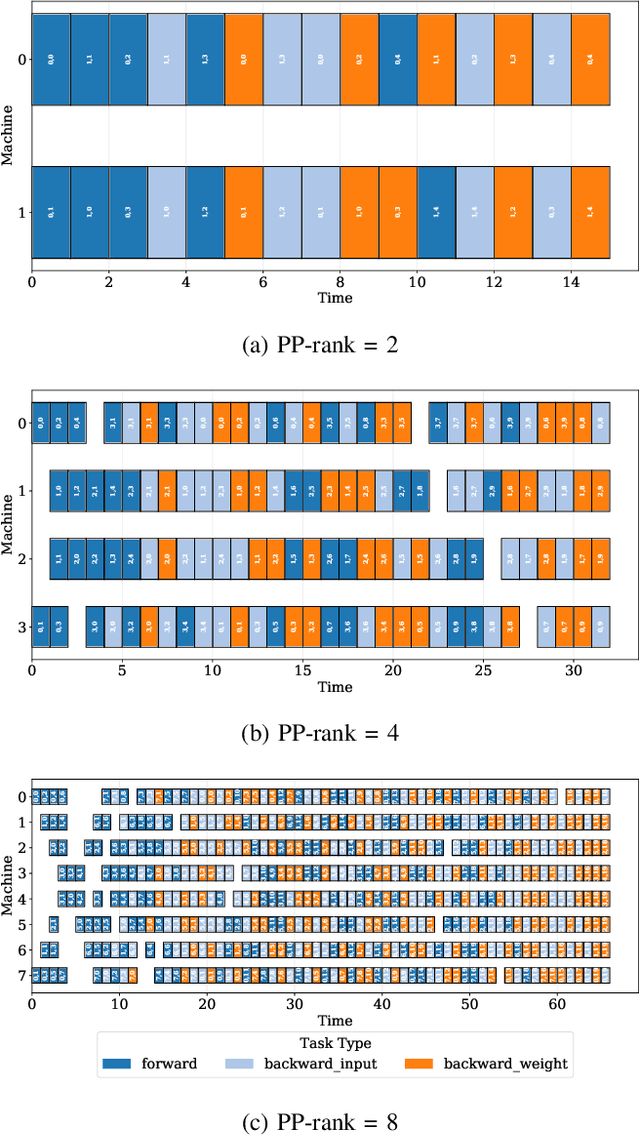
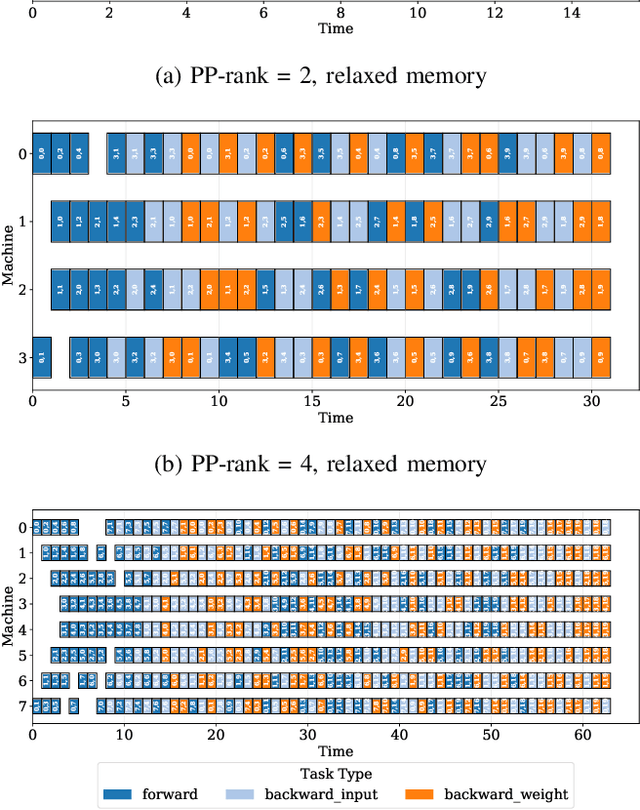
As the artificial intelligence community advances into the era of large models with billions of parameters, distributed training and inference have become essential. While various parallelism strategies-data, model, sequence, and pipeline-have been successfully implemented for popular neural networks on main-stream hardware, optimizing the distributed deployment schedule requires extensive expertise and manual effort. Further more, while existing frameworks with most simple chain-like structures, they struggle with complex non-linear architectures. Mixture-of-experts and multi-modal models feature intricate MIMO and branch-rich topologies that require fine-grained operator-level parallelization beyond the capabilities of existing frameworks. We propose formulating parallelism planning as a scheduling optimization problem using mixed-integer programming. We propose a bi-level solution framework balancing optimality with computational efficiency, automatically generating effective distributed plans that capture both the heterogeneous structure of modern neural networks and the underlying hardware constraints. In experiments comparing against expert-designed strategies like DeepSeek's DualPipe, our framework achieves comparable or superior performance, reducing computational bubbles by half under the same memory constraints. The framework's versatility extends beyond throughput optimization to incorporate hardware utilization maximization, memory capacity constraints, and other considerations or potential strategies. Such capabilities position our solution as both a valuable research tool for exploring optimal parallelization strategies and a practical industrial solution for large-scale AI deployment.

BPP-Search: Enhancing Tree of Thought Reasoning for Mathematical Modeling Problem Solving

LLMs exhibit advanced reasoning capabilities, offering the potential to transform natural language questions into mathematical models. However, existing open-source operations research datasets lack detailed annotations of the modeling process, such as variable definitions, focusing solely on objective values, which hinders reinforcement learning applications. To address this, we release the StructuredOR dataset, annotated with comprehensive labels that capture the complete mathematical modeling process. We further propose BPP-Search, a algorithm that integrates reinforcement learning into a tree-of-thought structure using Beam search, a Process reward model, and a pairwise Preference algorithm. This approach enables efficient exploration of tree structures, avoiding exhaustive search while improving accuracy. Extensive experiments on StructuredOR, NL4OPT, and MAMO-ComplexLP datasets show that BPP-Search significantly outperforms state-of-the-art methods, including Chain-of-Thought, Self-Consistency, and Tree-of-Thought. In tree-based reasoning, BPP-Search also surpasses Process Reward Model combined with Greedy or Beam Search, demonstrating superior accuracy and efficiency, and enabling faster retrieval of correct solutions.

Leveraging Large Language Models for Solving Rare MIP Challenges

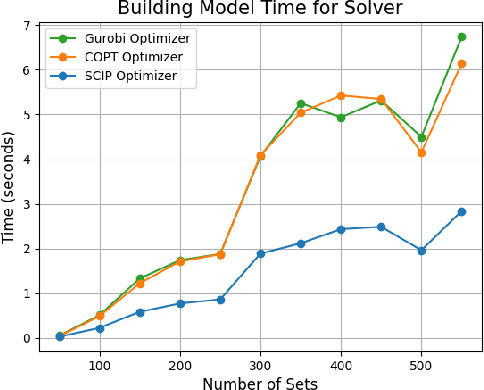
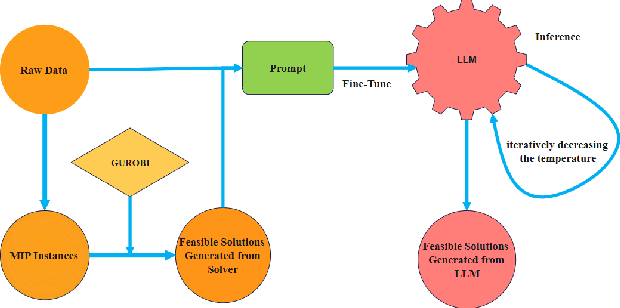
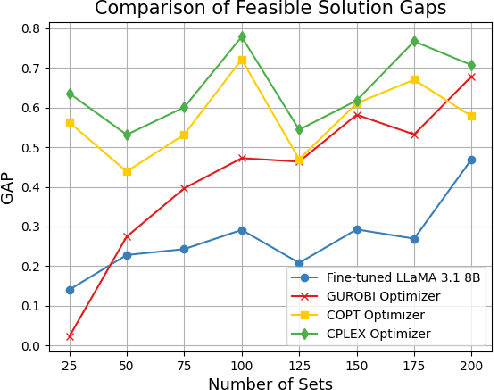
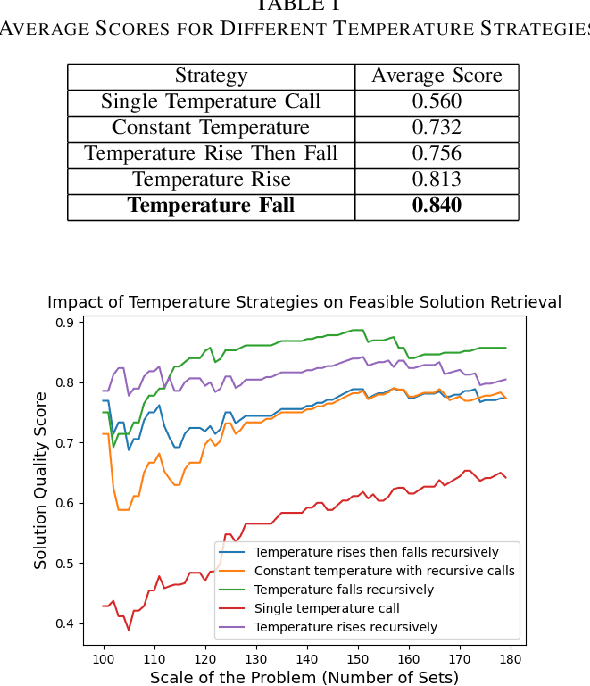
Mixed Integer Programming (MIP) has been extensively applied in areas requiring mathematical solvers to address complex instances within tight time constraints. However, as the problem scale increases, the complexity of model formulation and finding feasible solutions escalates significantly. In contrast, the model-building cost for end-to-end models, such as large language models (LLMs), remains largely unaffected by problem scale due to their pattern recognition capabilities. While LLMs, like GPT-4, without fine-tuning, can handle some traditional medium-scale MIP problems, they struggle with uncommon or highly specialized MIP scenarios. Fine-tuning LLMs can yield some feasible solutions for medium-scale MIP instances, but these models typically fail to explore diverse solutions when constrained by a low and constant temperature, limiting their performance. In this paper, we propose and evaluate a recursively dynamic temperature method integrated with a chain-of-thought approach. Our findings show that starting with a high temperature and gradually lowering it leads to better feasible solutions compared to other dynamic temperature strategies. Additionally, by comparing results generated by the LLM with those from Gurobi, we demonstrate that the LLM can produce solutions that complement traditional solvers by accelerating the pruning process and improving overall efficiency.