Ross L. Hatton
Asymmetric Friction in Geometric Locomotion
Dec 27, 2025Abstract:Geometric mechanics models of locomotion have provided insight into how robots and animals use environmental interactions to convert internal shape changes into displacement through the world, encoding this relationship in a ``motility map''. A key class of such motility maps arises from (possibly anisotropic) linear drag acting on the system's individual body parts, formally described via Riemannian metrics on the motions of the system's individual body parts. The motility map can then be generated by invoking a sub-Riemannian constraint on the aggregate system motion under which the position velocity induced by a given shape velocity is that which minimizes the power dissipated via friction. The locomotion of such systems is ``geometric'' in the sense that the final position reached by the system depends only on the sequence of shapes that the system passes through, but not on the rate with which the shape changes are made. In this paper, we consider a far more general class of systems in which the drag may be not only anisotropic (with different coefficients for forward/backward and left/right motions), but also asymmetric (with different coefficients for forward and backward motions). Formally, including asymmetry in the friction replaces the Riemannian metrics on the body parts with Finsler metrics. We demonstrate that the sub-Riemannian approach to constructing the system motility map extends naturally to a sub-Finslerian approach and identify system properties analogous to the constraint curvature of sub-Riemannian systems that allow for the characterization of the system motion capabilities.
Pose Estimation of a Thruster-Driven Bioinspired Multi-Link Robot
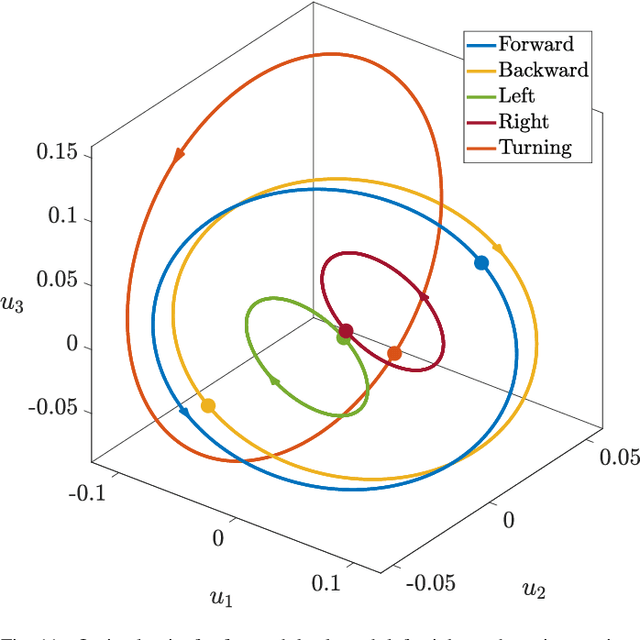
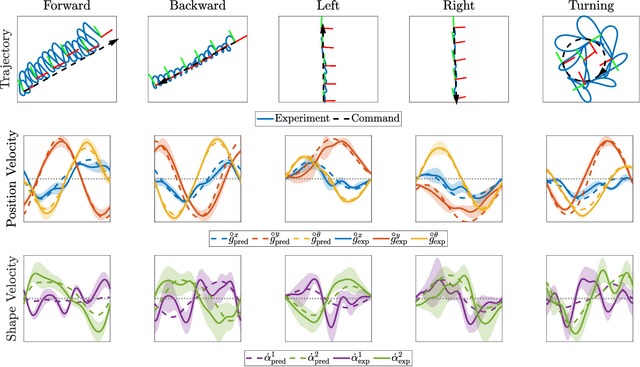
Oct 01, 2025Abstract:This work demonstrates pose (position and shape) estimation for a free-floating, bioinspired multi-link robot with unactuated joints, link-mounted thrusters for control, and a single gyroscope per link, resulting in an underactuated, minimally sensed platform. Through a proof-of-concept hardware experiment and offline Kalman filter analysis, we show that the robot's pose can be reliably estimated. State estimation is performed using an unscented Kalman filter augmented with Gaussian process residual learning to compensate for non-zero-mean, non-Gaussian noise. We further show that a filter trained on a multi-gait dataset (forward, backward, left, right, and turning) performs comparably to one trained on a larger forward-gait-only dataset when both are evaluated on the same forward-gait test trajectory. These results reveal overlap in the gait input space, which can be exploited to reduce training data requirements while enhancing the filter's generalizability across multiple gaits.
Geometric Gait Optimization for Kinodynamic Systems Using a Lie Group Integrator
Apr 27, 2025
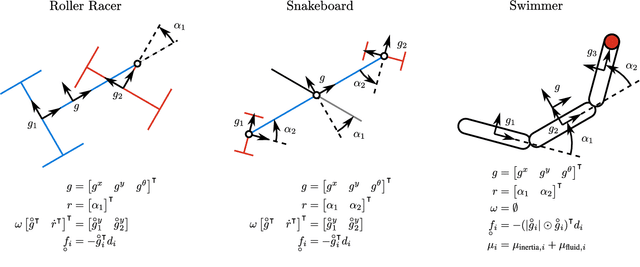
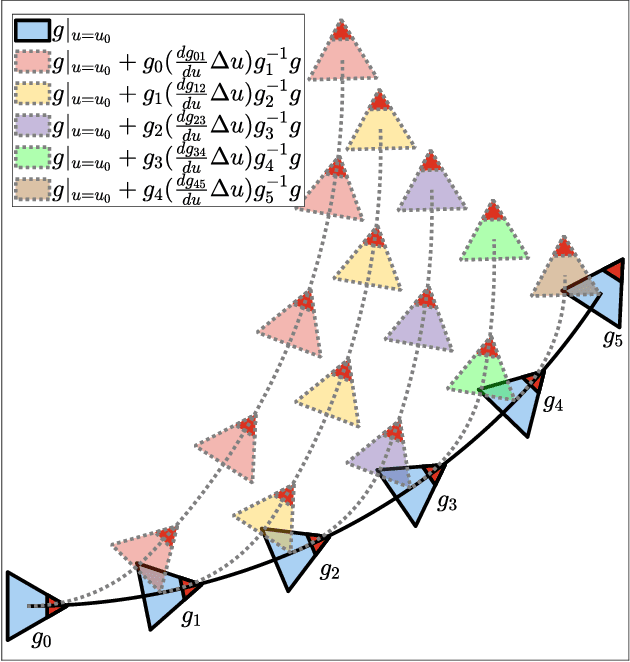
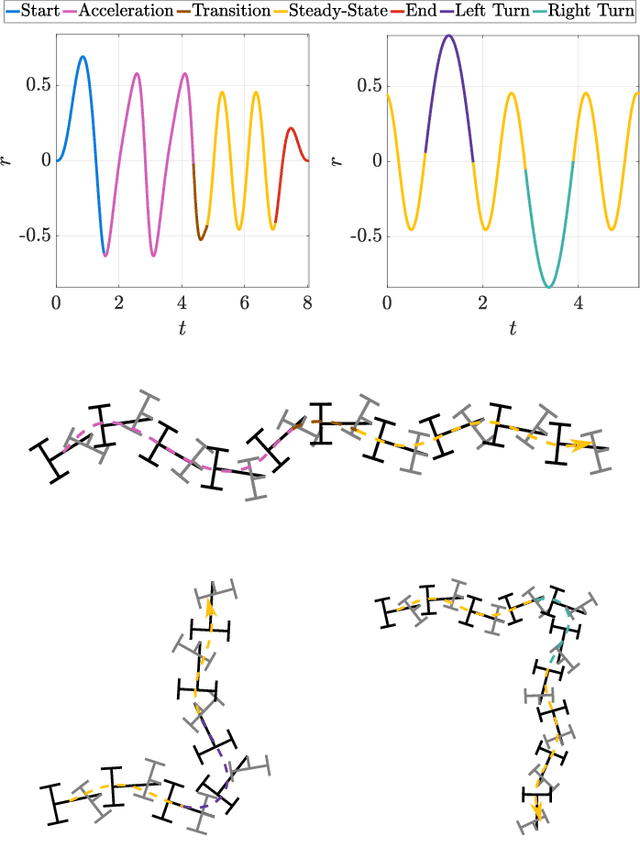
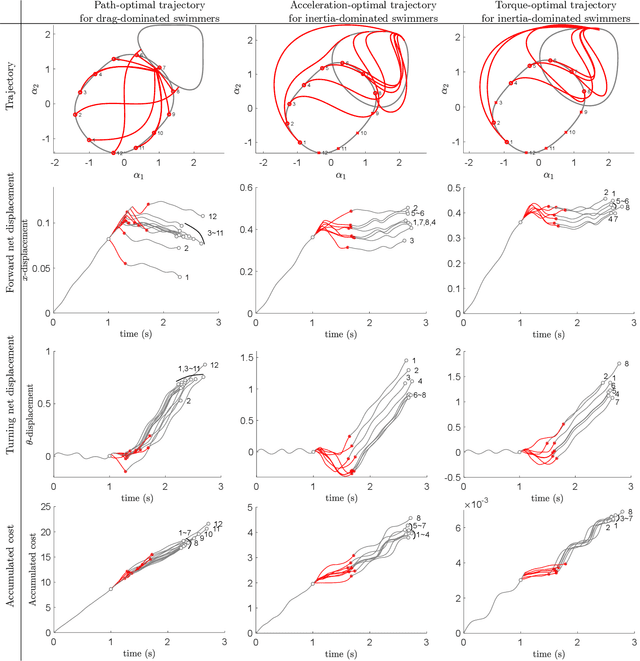
Abstract:This paper presents a gait optimization and motion planning framework for a class of locomoting systems with mixed kinematic and dynamic properties. Using Lagrangian reduction and differential geometry, we derive a general dynamic model that incorporates second-order dynamics and nonholonomic constraints, applicable to kinodynamic systems such as wheeled robots with nonholonomic constraints as well as swimming robots with nonisotropic fluid-added inertia and hydrodynamic drag. Building on Lie group integrators and group symmetries, we develop a variational gait optimization method for kinodynamic systems. By integrating multiple gaits and their transitions, we construct comprehensive motion plans that enable a wide range of motions for these systems. We evaluate our framework on three representative examples: roller racer, snakeboard, and swimmer. Simulation and hardware experiments demonstrate diverse motions, including acceleration, steady-state maintenance, gait transitions, and turning. The results highlight the effectiveness of the proposed method and its potential for generalization to other biological and robotic locomoting systems.
Geometric Data-Driven Multi-Jet Locomotion Inspired by Salps
Mar 11, 2025

Abstract:Salps are marine animals consisting of chains of jellyfish-like units. Their capacity for effective underwater undulatory locomotion through coordinating multi-jet propulsion has aroused significant interest in the field of robotics and inspired extensive research including design, modeling, and control. In this paper, we conduct a comprehensive analysis of the locomotion of salp-like systems using the robotic platform "LandSalp" based on geometric mechanics, including mechanism design, dynamic modeling, system identification, and motion planning and control. Our work takes a step toward a better understanding of salps' underwater locomotion and provides a clear path for extending these insights to more complex and capable underwater robotic systems. Furthermore, this study illustrates the effectiveness of geometric mechanics in bio-inspired robots for efficient data-driven locomotion modeling, demonstrated by learning the dynamics of LandSalp from only 3 minutes of experimental data. Lastly, we extend the geometric mechanics principles to multi-jet propulsion systems with stability considerations and validate the theory through experiments on the LandSalp hardware.
The Geometry of Optimal Gait Families for Steering Kinematic Locomoting Systems
Feb 24, 2025Abstract:Motion planning for locomotion systems typically requires translating high-level rigid-body tasks into low-level joint trajectories-a process that is straightforward for car-like robots with fixed, unbounded actuation inputs but more challenging for systems like snake robots, where the mapping depends on the current configuration and is constrained by joint limits. In this paper, we focus on generating continuous families of optimal gaits-collections of gaits parameterized by step size or steering rate-to enhance controllability and maneuverability. We uncover the underlying geometric structure of these optimal gait families and propose methods for constructing them using both global and local search strategies, where the local method and the global method compensate each other. The global search approach is robust to nonsmooth behavior, albeit yielding reduced-order solutions, while the local search provides higher accuracy but can be unstable near nonsmooth regions. To demonstrate our framework, we generate optimal gait families for viscous and perfect-fluid three-link swimmers. This work lays a foundation for integrating low-level joint controllers with higher-level motion planners in complex locomotion systems.
Geometric Optimal Control of Mechanical Systems with Gravitational and Resistive Force
Oct 12, 2024Abstract:Optimal control plays a crucial role in numerous mechanical and robotic applications. Broadly, optimal control methods are divided into direct methods (which optimize trajectories directly via discretization) and indirect methods (which transform optimality conditions into equations that guarantee optimal trajectories). While direct methods could mask geometric insights into system dynamics due to discretization, indirect methods offer a deeper understanding of the system's geometry. In this paper, we propose a geometric framework for understanding optimal control in mechanical systems, focusing on the combined effects of inertia, drag, and gravitational forces. By modeling mechanical systems as configuration manifolds equipped with kinetic and drag metrics, alongside a potential field, we explore how these factors influence trajectory optimization. We derive optimal control equations incorporating these effects and apply them to two-link and UR5 robotic manipulators, demonstrating how manifold curvature and resistive forces shape optimal trajectories. This work offers a comprehensive geometric approach to optimal control, with broad applications to robotic systems.
Optimal Control Approach for Gait Transition with Riemannian Splines
Sep 13, 2024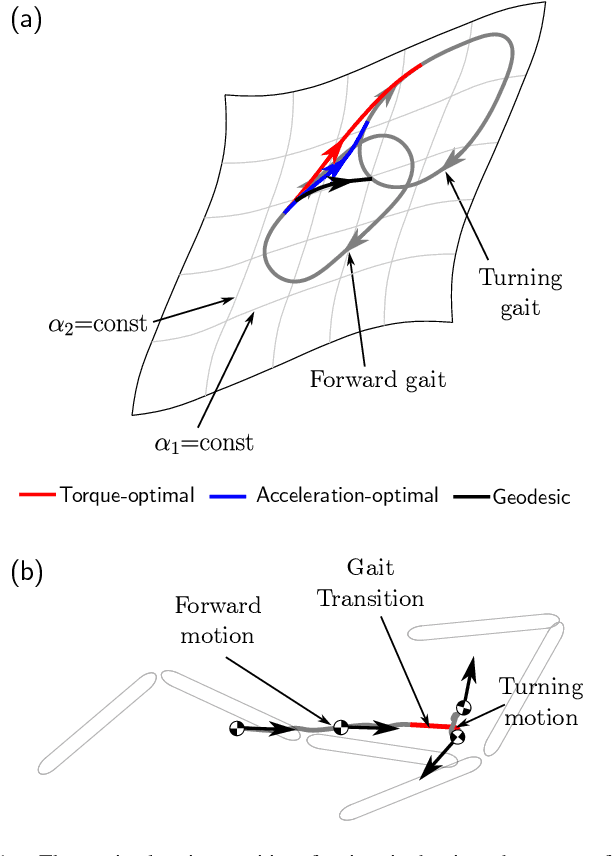
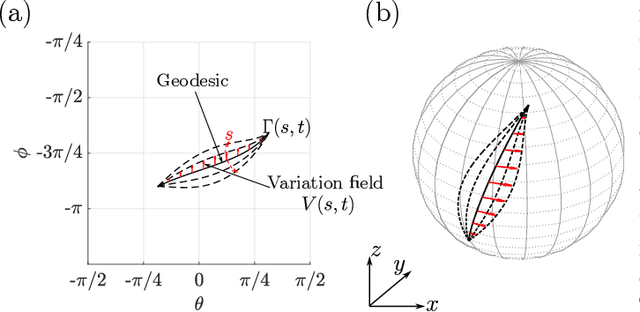
Abstract:Robotic locomotion often relies on sequenced gaits to efficiently convert control input into desired motion. Despite extensive studies on gait optimization, achieving smooth and efficient gait transitions remains challenging. In this paper, we propose a general solver based on geometric optimal control methods, leveraging insights from previous works on gait efficiency. Building upon our previous work, we express the effort to execute the trajectory as distinct geometric objects, transforming the optimization problems into boundary value problems. To validate our approach, we generate gait transition trajectories for three-link swimmers across various fluid environments. This work provides insights into optimal trajectory geometries and mechanical considerations for robotic locomotion.
Towards Geometric Motion Planning for High-Dimensional Systems: Gait-Based Coordinate Optimization and Local Metrics
Sep 16, 2023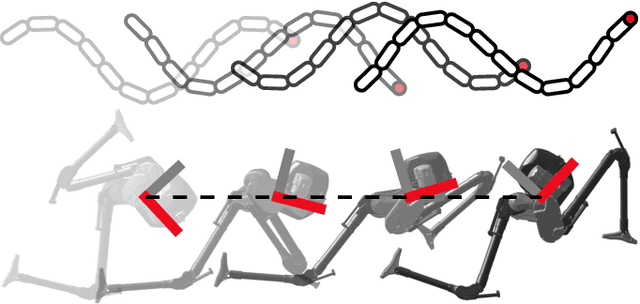
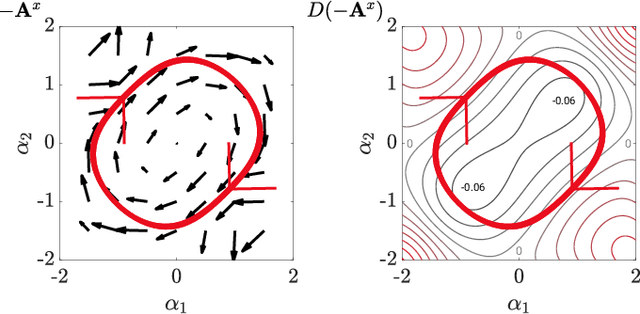
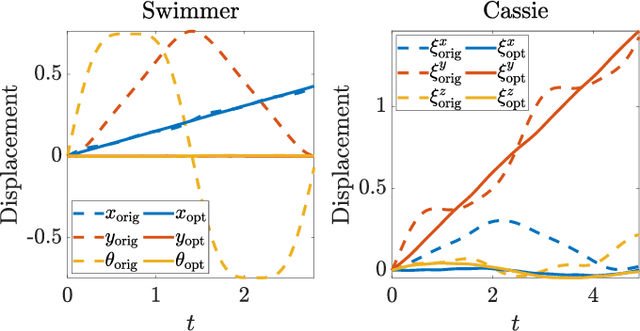
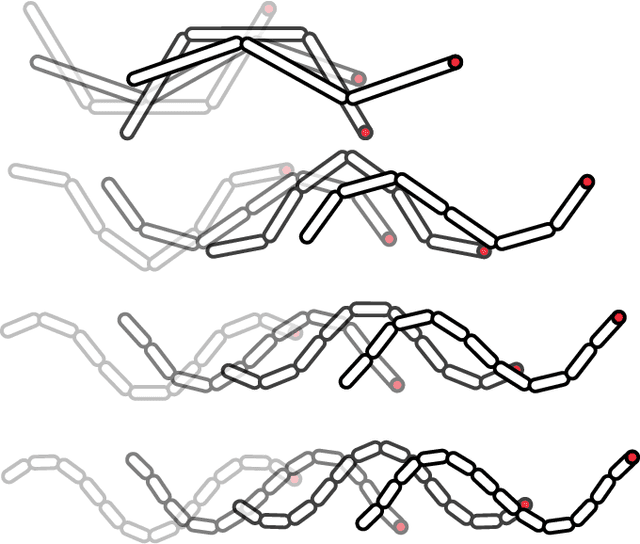
Abstract:Geometric motion planning offers effective and interpretable gait analysis and optimization tools for locomoting systems. However, due to the curse of dimensionality in coordinate optimization, a key component of geometric motion planning, it is almost infeasible to apply current geometric motion planning to high-dimensional systems. In this paper, we propose a gait-based coordinate optimization method that overcomes the curse of dimensionality. We also identify a unified geometric representation of locomotion by generalizing various nonholonomic constraints into local metrics. By combining these two approaches, we take a step towards geometric motion planning for high-dimensional systems. We test our method in two classes of high-dimensional systems - low Reynolds number swimmers and free-falling Cassie - with up to 11-dimensional shape variables. The resulting optimal gait in the high-dimensional system shows better efficiency compared to that of the reduced-order model. Furthermore, we provide a geometric optimality interpretation of the optimal gait.
Geometric Gait Optimization for Inertia-Dominated Systems With Nonzero Net Momentum
Sep 13, 2023

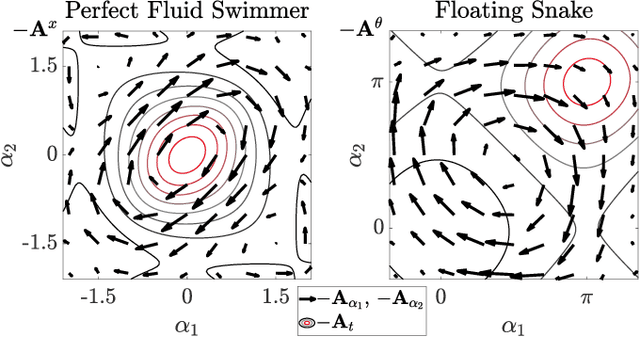
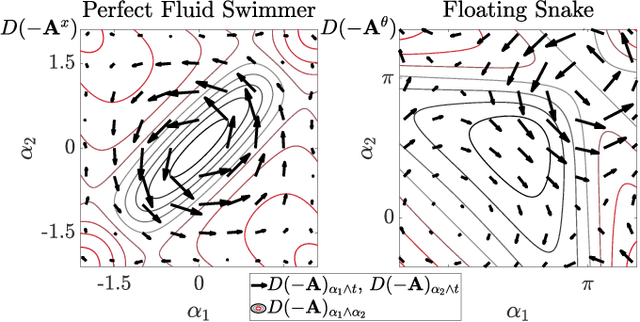
Abstract:Inertia-dominated mechanical systems can achieve net displacement by 1) periodically changing their shape (known as kinematic gait) and 2) adjusting their inertia distribution to utilize the existing nonzero net momentum (known as momentum gait). Therefore, finding the gait that most effectively utilizes the two types of locomotion in terms of the magnitude of the net momentum is a significant topic in the study of locomotion. For kinematic locomotion with zero net momentum, the geometry of optimal gaits is expressed as the equilibria of system constraint curvature flux through the surface bounded by the gait, and the cost associated with executing the gait in the metric space. In this paper, we identify the geometry of optimal gaits with nonzero net momentum effects by lifting the gait description to a time-parameterized curve in shape-time space. We also propose the variational gait optimization algorithm corresponding to the lifted geometric structure, and identify two distinct patterns in the optimal motion, determined by whether or not the kinematic and momentum gaits are concentric. The examples of systems with and without fluid-added mass demonstrate that the proposed algorithm can efficiently solve forward and turning locomotion gaits in the presence of nonzero net momentum. At any given momentum and effort limit, the proposed optimal gait that takes into account both momentum and kinematic effects outperforms the reference gaits that each only considers one of these effects.
Geometric Mechanics of Contact-Switching Systems
Jun 17, 2023Abstract:Discrete and periodic contact switching is a key characteristic of steady state legged locomotion. This paper introduces a framework for modeling and analyzing this contact-switching behavior through the framework of geometric mechanics on a toy robot model that can make continuous limb swings and discrete contact switches. The kinematics of this model forms a hybrid shape space and by extending the generalized Stokes' theorem to compute discrete curvature functions called stratified panels, we determine average locomotion generated by gaits spanning multiple contact modes. Using this tool, we also demonstrate the ability to optimize gaits based on system's locomotion constraints and perform gait reduction on a complex gait spanning multiple contact modes to highlight the scalability to multilegged systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge