The Geometry of Optimal Gait Families for Steering Kinematic Locomoting Systems

Motion planning for locomotion systems typically requires translating high-level rigid-body tasks into low-level joint trajectories-a process that is straightforward for car-like robots with fixed, unbounded actuation inputs but more challenging for systems like snake robots, where the mapping depends on the current configuration and is constrained by joint limits. In this paper, we focus on generating continuous families of optimal gaits-collections of gaits parameterized by step size or steering rate-to enhance controllability and maneuverability. We uncover the underlying geometric structure of these optimal gait families and propose methods for constructing them using both global and local search strategies, where the local method and the global method compensate each other. The global search approach is robust to nonsmooth behavior, albeit yielding reduced-order solutions, while the local search provides higher accuracy but can be unstable near nonsmooth regions. To demonstrate our framework, we generate optimal gait families for viscous and perfect-fluid three-link swimmers. This work lays a foundation for integrating low-level joint controllers with higher-level motion planners in complex locomotion systems.

Adaptive Gait Modeling and Optimization for Principally Kinematic Systems

Robotic adaptation to unanticipated operating conditions is crucial to achieving persistence and robustness in complex real world settings. For a wide range of cutting-edge robotic systems, such as micro- and nano-scale robots, soft robots, medical robots, and bio-hybrid robots, it is infeasible to anticipate the operating environment a priori due to complexities that arise from numerous factors including imprecision in manufacturing, chemo-mechanical forces, and poorly understood contact mechanics. Drawing inspiration from data-driven modeling, geometric mechanics (or gauge theory), and adaptive control, we employ an adaptive system identification framework and demonstrate its efficacy in enhancing the performance of principally kinematic locomotors (those governed by Rayleigh dissipation or zero momentum conservation). We showcase the capability of the adaptive model to efficiently accommodate varying terrains and iteratively modified behaviors within a behavior optimization framework. This provides both the ability to improve fundamental behaviors and perform motion tracking to precision. Notably, we are capable of optimizing the gaits of the Purcell swimmer using approximately 10 cycles per link, which for the nine-link Purcell swimmer provides a factor of ten improvement in optimization speed over the state of the art. Beyond simply a computational speed up, this ten-fold improvement may enable this method to be successfully deployed for in-situ behavior refinement, injury recovery, and terrain adaptation, particularly in domains where simulations provide poor guides for the real world.

A Data-Driven Approach to Geometric Modeling of Systems with Low-Bandwidth Actuator Dynamics

It is challenging to perform identification on soft robots due to their underactuated, high dimensional dynamics. In this work, we present a data-driven modeling framework, based on geometric mechanics (also known as gauge theory), that can be applied to systems with low-bandwidth actuation of the shape space. By exploiting temporal asymmetries in actuator dynamics, our approach enables the design of robots that can be driven by a single control input. We present a method for constructing a series connected model comprising actuator and locomotor dynamics based on data points from stochastically perturbed, repeated behaviors around the observed limit cycle. We demonstrate our methods on a real-world example of a soft crawler made by stimuli-responsive hydrogels that locomotes on merely one cycling control signal by utilizing its geometric and temporal asymmetry. For systems with first-order, low-pass actuator dynamics, such as swelling-driven actuators used in hydrogel crawlers, we show that first order Taylor approximations can well capture the dynamics of the system shape as well as its movements. Finally, we propose an approach of numerically optimizing control signals by iteratively refining models and optimizing the input waveform.

Prospective Learning: Back to the Future

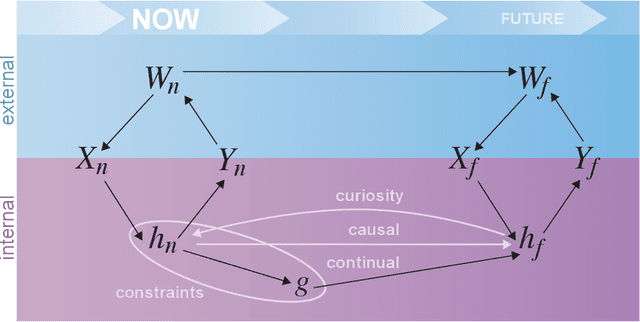
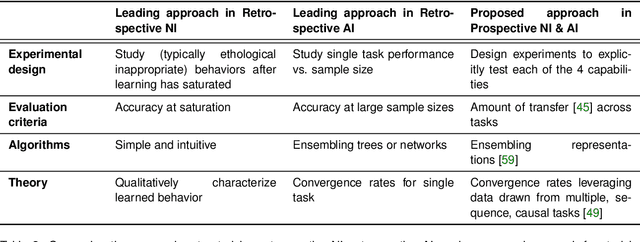
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.

Identification of a Hybrid Spring Mass Damper via Harmonic Transfer Functions as a Step Towards Data-Driven Models for Legged Locomotion

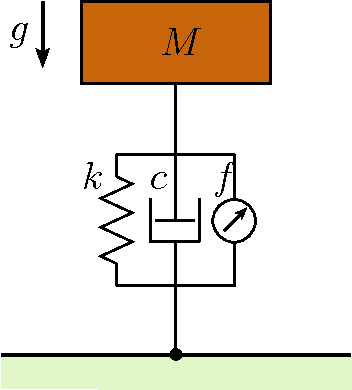
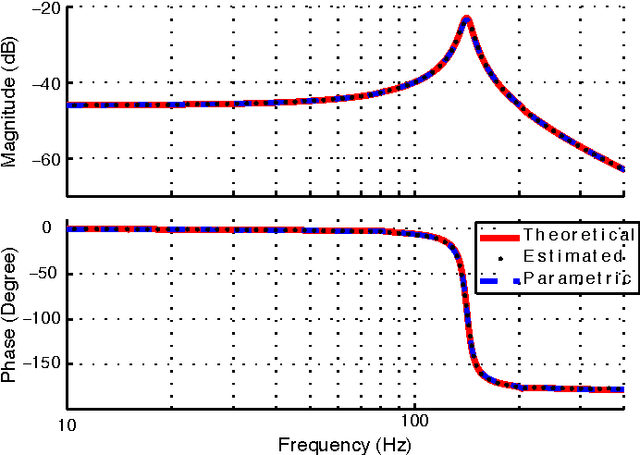
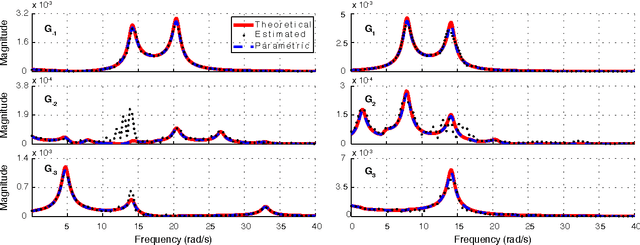
There are limitations on the extent to which manually constructed mathematical models can capture relevant aspects of legged locomotion. Even simple models for basic behaviors such as running involve non-integrable dynamics, requiring the use of possibly inaccurate approximations in the design of model-based controllers. In this study, we show how data-driven frequency domain system identification methods can be used to obtain input--output characteristics for a class of dynamical systems around their limit cycles, with hybrid structural properties similar to those observed in legged locomotion systems. Under certain assumptions, we can approximate hybrid dynamics of such systems around their limit cycle as a piecewise smooth linear time periodic system (LTP), further approximated as a time-periodic, piecewise LTI system to reduce parametric degrees of freedom in the identification process. In this paper, we use a simple one-dimensional hybrid model in which a limit-cycle is induced through the actions of a linear actuator to illustrate the details of our method. We first derive theoretical harmonic transfer functions of our example model. We then excite the model with small chirp signals to introduce perturbations around its limit-cycle and present systematic identification results to estimate the harmonic transfer functions for this model. Comparison between the data-driven HTF model and its theoretical prediction illustrates the potential effectiveness of such empirical identification methods in legged locomotion.