Adaptive Control of Underactuated Planar Pronking Hexapod

Underactuated legged robots depict highly nonlinear and complex dynamical behaviors that create significant challenges in accurately modeling system dynamics using both first principles and system identification approaches. Hence, it makes a more substantial challenge to design stabilizing controllers. If physical parameters on mathematical models have miscalibrations due to uncertainty in identifying and modeling processes, designed controllers could perform poorly or even result in unstable responses. Moreover, these parameters can certainly change-over-time due to operation and environmental conditions. In that respect, analogous to a living organism modifying its behavior in response to novel conditions, adapting/updating system parameters, such as spring constant, to compensate for modeling errors could provide the advantage of constructing a stable gait level controller without needing "exact" dynamical parameter values. This paper presents an online, model-based adaptive control approach for an underactuated planar hexapod robot's pronking behavior adopted from antelope species. We show through systematic simulation studies that the adaptive control policy is robust to high levels of parameter uncertainties compared to a non-adaptive model-based dead-beat controller.

Identification of a Hybrid Spring Mass Damper via Harmonic Transfer Functions as a Step Towards Data-Driven Models for Legged Locomotion

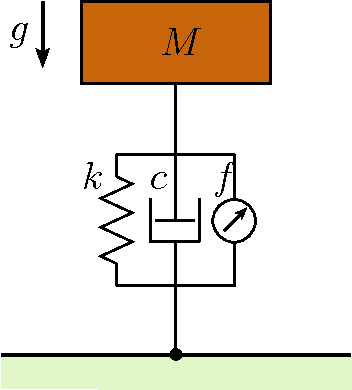
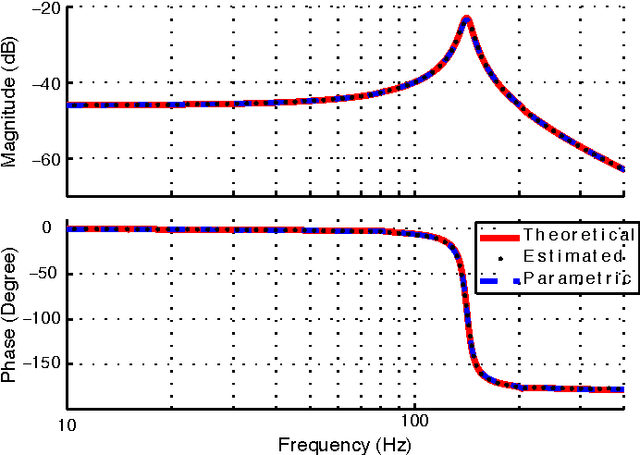
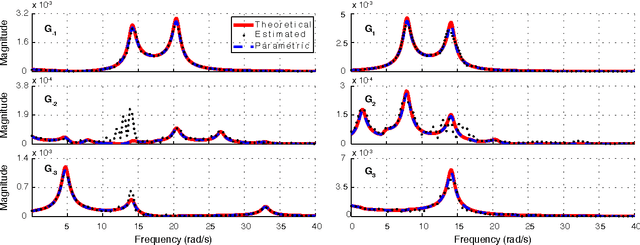
There are limitations on the extent to which manually constructed mathematical models can capture relevant aspects of legged locomotion. Even simple models for basic behaviors such as running involve non-integrable dynamics, requiring the use of possibly inaccurate approximations in the design of model-based controllers. In this study, we show how data-driven frequency domain system identification methods can be used to obtain input--output characteristics for a class of dynamical systems around their limit cycles, with hybrid structural properties similar to those observed in legged locomotion systems. Under certain assumptions, we can approximate hybrid dynamics of such systems around their limit cycle as a piecewise smooth linear time periodic system (LTP), further approximated as a time-periodic, piecewise LTI system to reduce parametric degrees of freedom in the identification process. In this paper, we use a simple one-dimensional hybrid model in which a limit-cycle is induced through the actions of a linear actuator to illustrate the details of our method. We first derive theoretical harmonic transfer functions of our example model. We then excite the model with small chirp signals to introduce perturbations around its limit-cycle and present systematic identification results to estimate the harmonic transfer functions for this model. Comparison between the data-driven HTF model and its theoretical prediction illustrates the potential effectiveness of such empirical identification methods in legged locomotion.