Geometric Data-Driven Multi-Jet Locomotion Inspired by Salps

Salps are marine animals consisting of chains of jellyfish-like units. Their capacity for effective underwater undulatory locomotion through coordinating multi-jet propulsion has aroused significant interest in the field of robotics and inspired extensive research including design, modeling, and control. In this paper, we conduct a comprehensive analysis of the locomotion of salp-like systems using the robotic platform "LandSalp" based on geometric mechanics, including mechanism design, dynamic modeling, system identification, and motion planning and control. Our work takes a step toward a better understanding of salps' underwater locomotion and provides a clear path for extending these insights to more complex and capable underwater robotic systems. Furthermore, this study illustrates the effectiveness of geometric mechanics in bio-inspired robots for efficient data-driven locomotion modeling, demonstrated by learning the dynamics of LandSalp from only 3 minutes of experimental data. Lastly, we extend the geometric mechanics principles to multi-jet propulsion systems with stability considerations and validate the theory through experiments on the LandSalp hardware.

The Geometry of Optimal Gait Families for Steering Kinematic Locomoting Systems

Motion planning for locomotion systems typically requires translating high-level rigid-body tasks into low-level joint trajectories-a process that is straightforward for car-like robots with fixed, unbounded actuation inputs but more challenging for systems like snake robots, where the mapping depends on the current configuration and is constrained by joint limits. In this paper, we focus on generating continuous families of optimal gaits-collections of gaits parameterized by step size or steering rate-to enhance controllability and maneuverability. We uncover the underlying geometric structure of these optimal gait families and propose methods for constructing them using both global and local search strategies, where the local method and the global method compensate each other. The global search approach is robust to nonsmooth behavior, albeit yielding reduced-order solutions, while the local search provides higher accuracy but can be unstable near nonsmooth regions. To demonstrate our framework, we generate optimal gait families for viscous and perfect-fluid three-link swimmers. This work lays a foundation for integrating low-level joint controllers with higher-level motion planners in complex locomotion systems.

Geometric analysis of gaits and optimal control for three-link kinematic swimmers

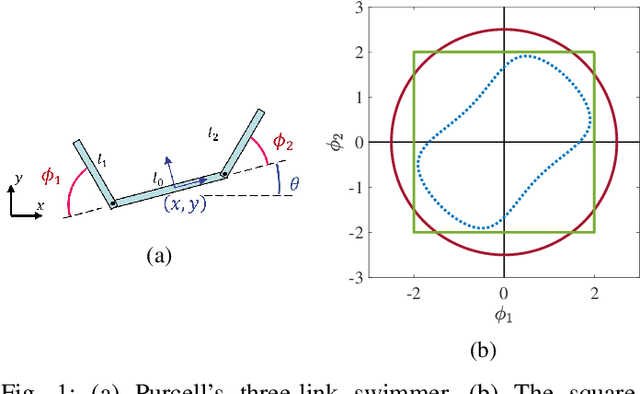
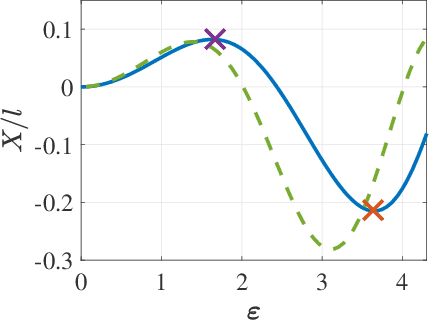
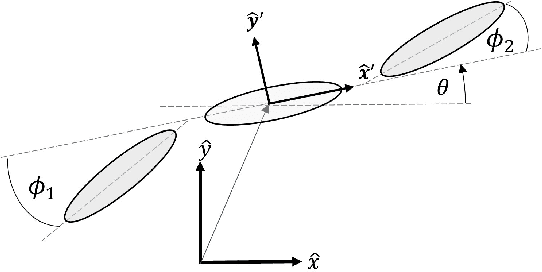
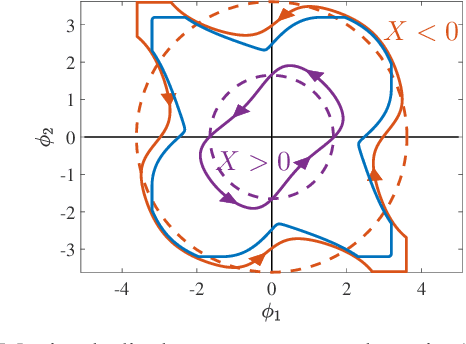
Many robotic systems locomote using gaits - periodic changes of internal shape, whose mechanical interaction with the robot`s environment generate characteristic net displacements. Prominent examples with two shape variables are the low Reynolds number 3-link "Purcell swimmer" with inputs of 2 joint angles and the "ideal fluid" swimmer. Gait analysis of these systems allows for intelligent decisions to be made about the swimmer`s locomotive properties, increasing the potential for robotic autonomy. In this work, we present comparative analysis of gait optimization using two different methods. The first method is variational approach of "Pontryagin`s maximum principle" (PMP) from optimal control theory. We apply PMP for several variants of 3-link swimmers, with and without incorporation of bounds on joint angles. The second method is differential-geometric analysis of the gaits based on curvature (total Lie bracket) of the local connection for 3-link swimmers. Using optimized body-motion coordinates, contour plots of the curvature in shape space gives visualization that enables identifying distance-optimal gaits as zero level sets. Combining and comparing results of the two methods enables better understanding of changes in existence, shape and topology of distance-optimal gait trajectories, depending on the swimmers' parameters.