Yizhar Or
Analysis and experiments of the dissipative Twistcar: direction reversal and asymptotic approximations
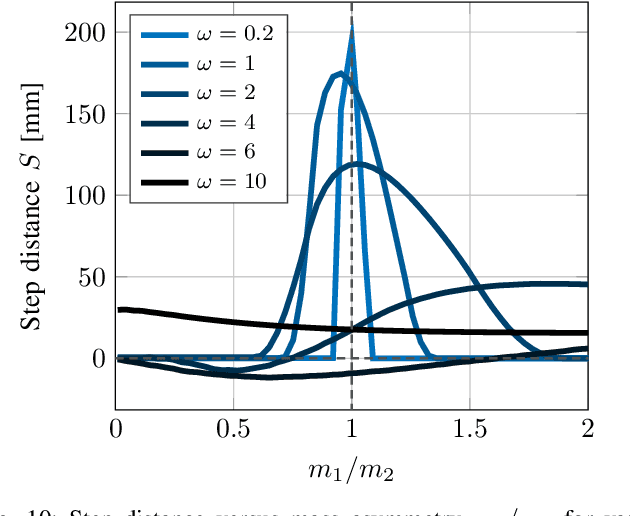
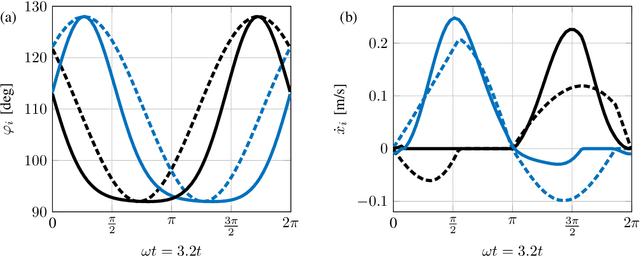
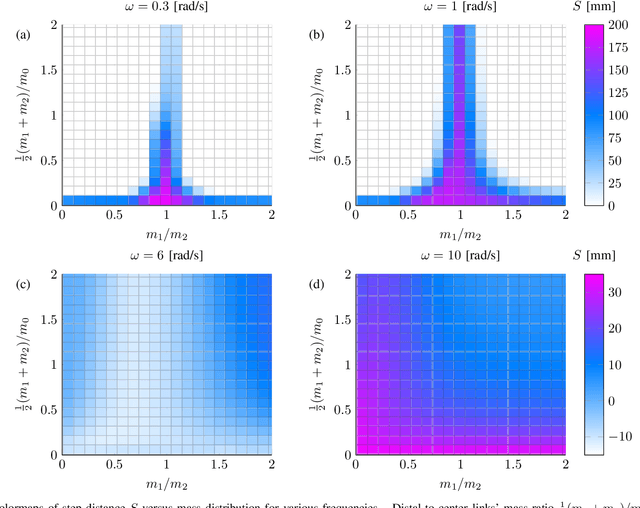
Jun 23, 2025Abstract:Underactuated wheeled vehicles are commonly studied as nonholonomic systems with periodic actuation. Twistcar is a classical example inspired by a riding toy, which has been analyzed using a planar model of a dynamical system with nonholonomic constraints. Most of the previous analyses did not account for energy dissipation due to friction. In this work, we study a theoretical two-link model of the Twistcar while incorporating dissipation due to rolling resistance. We obtain asymptotic expressions for the system's small-amplitude steady-state periodic dynamics, which reveals the possibility of reversing the direction of motion upon varying the geometric and mass properties of the vehicle. Next, we design and construct a robotic prototype of the Twistcar whose center-of-mass position can be shifted by adding and removing a massive block, enabling demonstration of the Twistcar's direction reversal phenomenon. We also conduct parameter fitting for the frictional resistance in order to improve agreement with experiments.
Locomotion Dynamics of an Underactuated Three-Link Robotic Vehicle
Jul 31, 2024Abstract:The wheeled three-link snake robot is a well-known example of an underactuated system modelled using nonholonomic constraints, preventing lateral slippage (skid) of the wheels. A kinematically controlled configuration assumes that both joint angles are directly prescribed as phase-shifted periodic input. In another configuration of the robot, only one joint is periodically actuated while the second joint is passively governed by a visco-elastic torsion spring. In our work, we constructed the two configurations of the wheeled robot and conducted motion experiments under different actuation inputs. Analysis of the motion tracking measurements reveals a significant amount of wheels' skid, in contrast to the assumptions used in standard nonholonomic models. Therefore, we propose modified dynamic models which include wheels' skid and viscous friction forces, as well as rolling resistance. After parameter fitting, these dynamic models reach good agreement with the motion measurements, including effects of input's frequency on the mean speed and net displacement per period. This illustrates the importance of incorporating wheels' skid and friction into the system's model.
Multistable Physical Neural Networks
May 31, 2024Abstract:Artificial neural networks (ANNs), which are inspired by the brain, are a central pillar in the ongoing breakthrough in artificial intelligence. In recent years, researchers have examined mechanical implementations of ANNs, denoted as Physical Neural Networks (PNNs). PNNs offer the opportunity to view common materials and physical phenomena as networks, and to associate computational power with them. In this work, we incorporated mechanical bistability into PNNs, enabling memory and a direct link between computation and physical action. To achieve this, we consider an interconnected network of bistable liquid-filled chambers. We first map all possible equilibrium configurations or steady states, and then examine their stability. Building on these maps, both global and local algorithms for training multistable PNNs are implemented. These algorithms enable us to systematically examine the network's capability to achieve stable output states and thus the network's ability to perform computational tasks. By incorporating PNNs and multistability, we can design structures that mechanically perform tasks typically associated with electronic neural networks, while directly obtaining physical actuation. The insights gained from our study pave the way for the implementation of intelligent structures in smart tech, metamaterials, medical devices, soft robotics, and other fields.
Geometric analysis of gaits and optimal control for three-link kinematic swimmers
Sep 14, 2021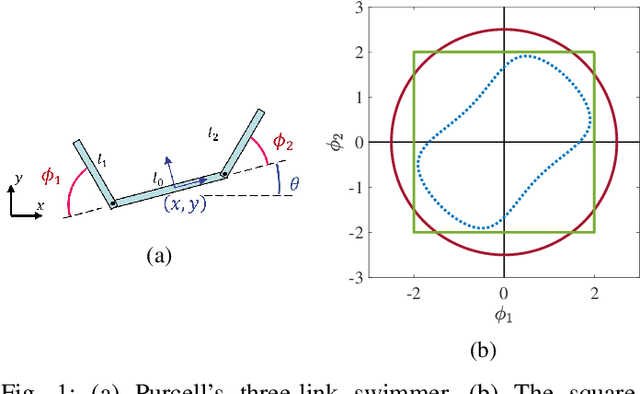
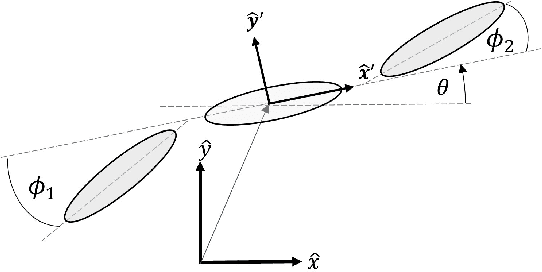
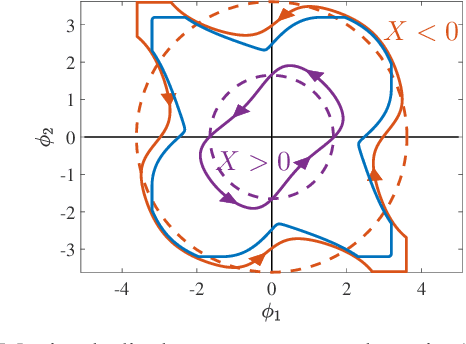
Abstract:Many robotic systems locomote using gaits - periodic changes of internal shape, whose mechanical interaction with the robot`s environment generate characteristic net displacements. Prominent examples with two shape variables are the low Reynolds number 3-link "Purcell swimmer" with inputs of 2 joint angles and the "ideal fluid" swimmer. Gait analysis of these systems allows for intelligent decisions to be made about the swimmer`s locomotive properties, increasing the potential for robotic autonomy. In this work, we present comparative analysis of gait optimization using two different methods. The first method is variational approach of "Pontryagin`s maximum principle" (PMP) from optimal control theory. We apply PMP for several variants of 3-link swimmers, with and without incorporation of bounds on joint angles. The second method is differential-geometric analysis of the gaits based on curvature (total Lie bracket) of the local connection for 3-link swimmers. Using optimized body-motion coordinates, contour plots of the curvature in shape space gives visualization that enables identifying distance-optimal gaits as zero level sets. Combining and comparing results of the two methods enables better understanding of changes in existence, shape and topology of distance-optimal gait trajectories, depending on the swimmers' parameters.
Experimental Verification of Stability Theory for a Planar Rigid Body with Two Unilateral Frictional Contacts
Aug 24, 2020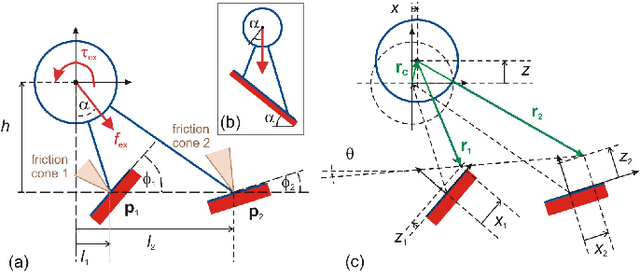
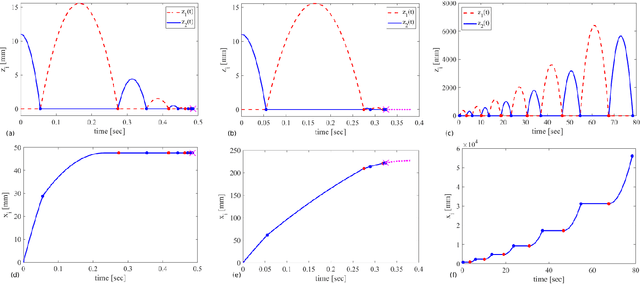
Abstract:Stability of equilibrium states in mechanical systems with multiple unilateral frictional contacts is an important practical requirement, with high relevance for robotic applications. In our previous work, we theoretically analyzed finite-time Lyapunov stability for a minimal model of planar rigid body with two frictional point contacts. Assuming inelastic impacts and Coulomb friction, conditions for stability and instability of an equilibrium configuration have been derived. In this work, we present for the first time an experimental demonstration of this stability theory, using a variable-structure rigid ''biped'' with frictional footpads on an inclined plane. By changing the biped's center-of-mass location, we attain different equilibrium states, which respond to small perturbations by divergence or convergence, showing remarkable agreement with the predictions of the stability theory. Using high-speed recording of video movies, good quantitative agreement between experiments and numerical simulations is obtained, and limitations of the rigid-body model and inelastic impact assumptions are also studied. The results prove the utility and practical value of our stability theory.
Inertial Inchworm Crawling
Jun 03, 2020
Abstract:Inchworm crawling allows for both quasistatic and dynamic gaits at a wide range of actuation frequencies. This locomotion mechanism is common in nonskeletal animals and exploited extensively in the bio-inspired field of soft robotics. In this work we develop and simulate the hybrid dynamic crawling of a three-link robot, with passive frictional contacts. We fabricate and experimentally test such robot under periodic inputs of joints' angles, with good agreement to the theoretical predictions. This allows to comprehend and exploit the effects of inertia in order to find optimal performance in inputs' parameters. A simple criterion of robustness to uncertainties in friction is proposed. Tuning the inputs according to this criterion improves the robustness of low-frequency actuation, while increasing the frequency allows for gaits with both high advancement velocity and robustness. Finally, the advantages of uneven mass distribution are studied. Time-scaling technique is introduced to shape inputs that achieve similar effect without reassembling the robot. A machine-learning based optimization is applied to these inputs to further improve the robot's performance.
Understanding Legged Crawling for Soft-Robotics
Nov 17, 2019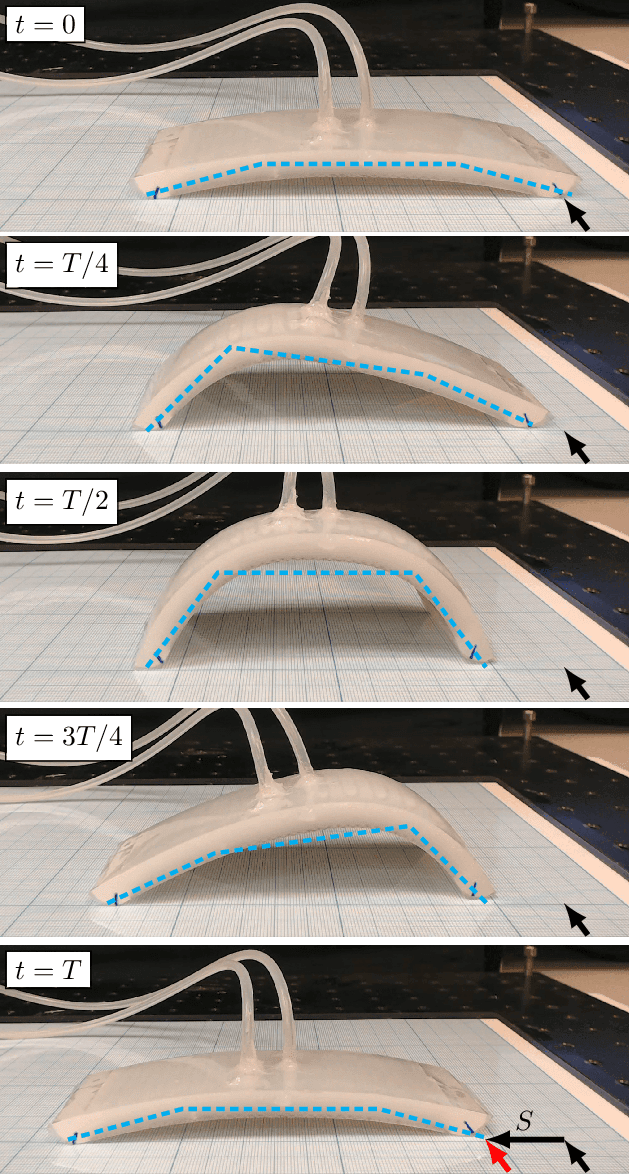
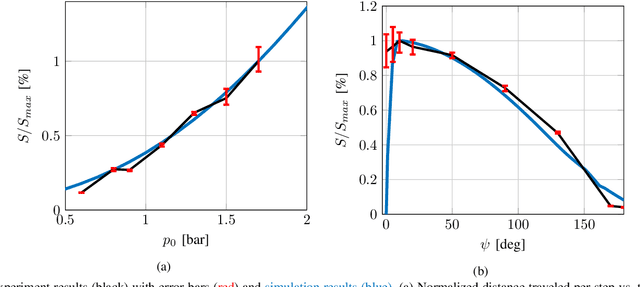
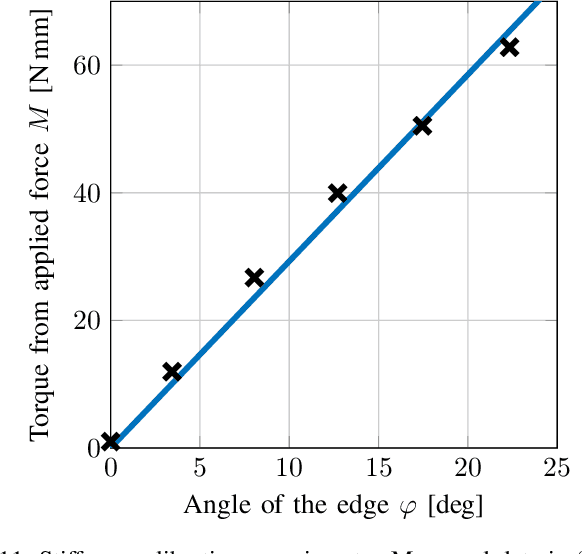
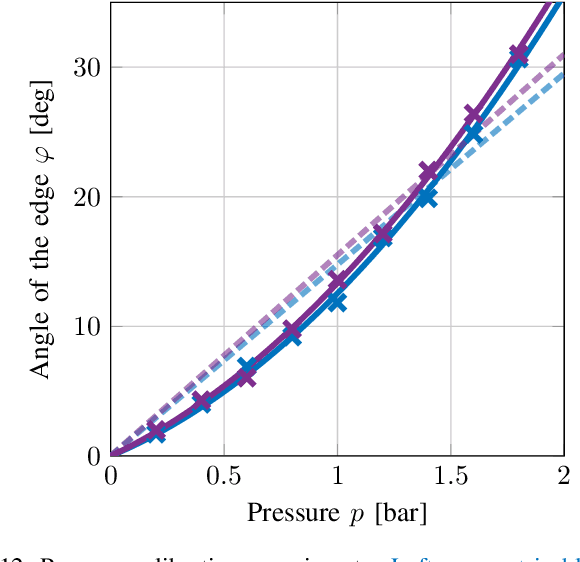
Abstract:Crawling is a common locomotion mechanism in soft robots and nonskeletal animals. In this work we propose modeling soft-robotic legged locomotion by approximating it with an equivalent articulated robot with elastic joints. For concreteness we study our soft robot with two bending actuators via an articulated three-link model. The solution of statically indeterminate systems with stick-slip contact transitions requires for a novel hybrid-quasitatic analysis. Then, we utilize our analysis to investigate the influence of phase-shifted harmonic inputs on performance of crawling gaits, including sensitivity analysis to friction uncertainties and energetic cost of transport. We achieve optimal values of gait parameters. Finally, we fabricate and test a fluid-driven soft robot. The experiments display remarkable agreement with the theoretical analysis, proving that our simple model correctly captures and explains the fundamental principles of inchworm crawling and can be applied to other soft-robotic legged robots.
Dynamic Walking on Slippery Surfaces: Demonstrating Stable Bipedal Gaits with Planned Ground Slippage
Dec 11, 2018
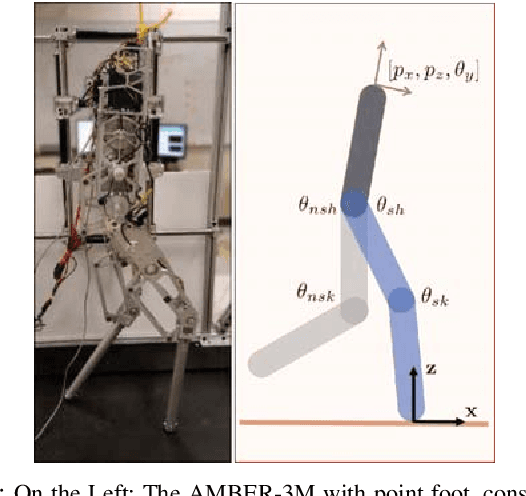
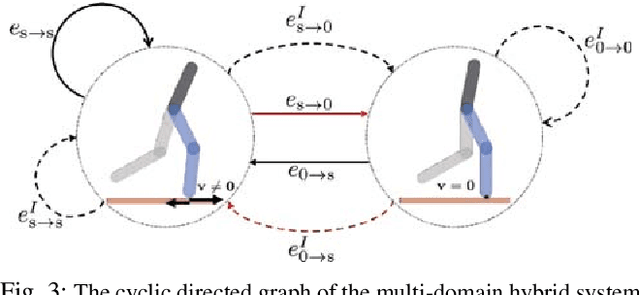
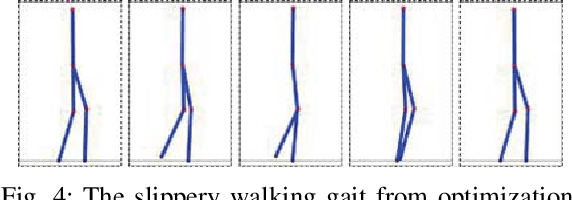
Abstract:Dynamic bipedal robot locomotion has achieved remarkable success due in part to recent advances in trajectory generation and nonlinear control for stabilization. A key assumption utilized in both theory and experiments is that the robot's stance foot always makes no-slip contact with the ground, including at impacts. This assumption breaks down on slippery low-friction surfaces, as commonly encountered in outdoor terrains, leading to failure and loss of stability. In this work, we extend the theoretical analysis and trajectory optimization to account for stick-slip transitions at point foot contact using Coulomb's friction law. Using AMBER-3M planar biped robot as an experimental platform, we demonstrate for the first time a slippery walking gait which can be stabilized successfully both on a lubricated surface and on a rough no-slip surface. We also study the influence of foot slippage on reducing the mechanical cost of transport, and compare energy efficiency in both numerical simulations and experimental measurements.
Lyapunov stability of a rigid body with two frictional contacts
Aug 09, 2016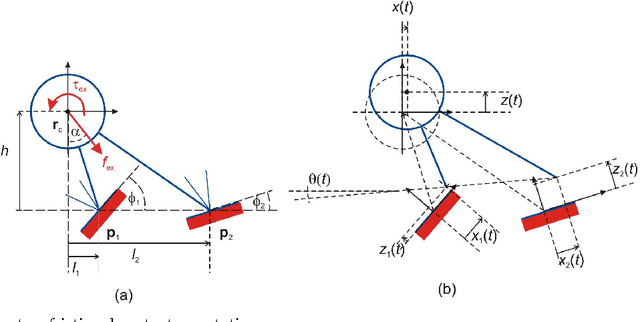
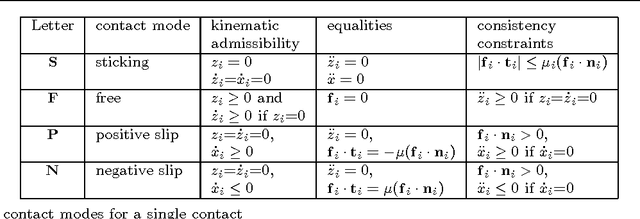
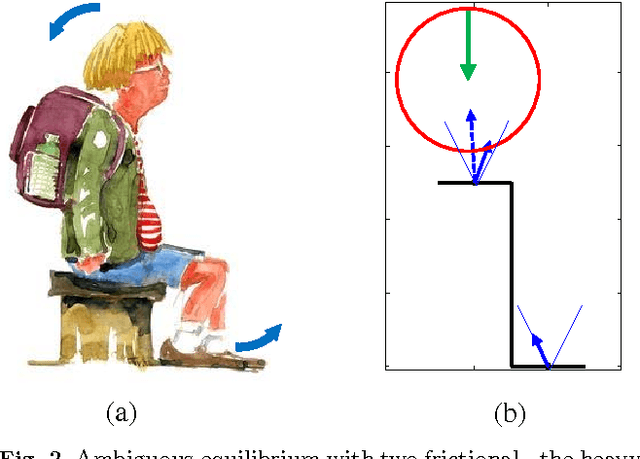
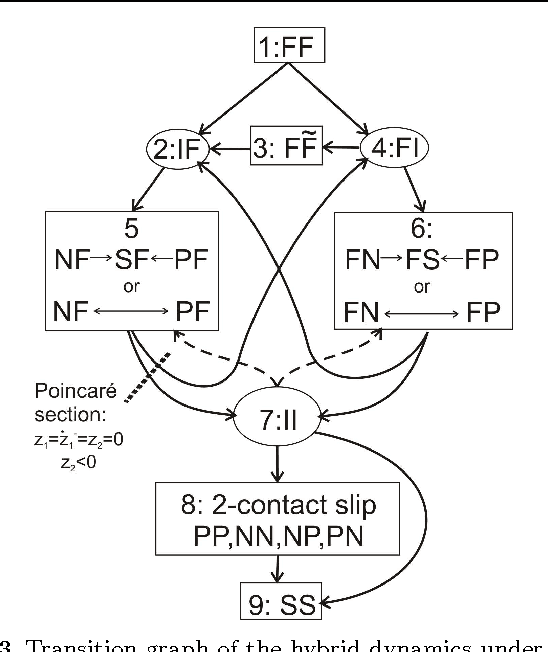
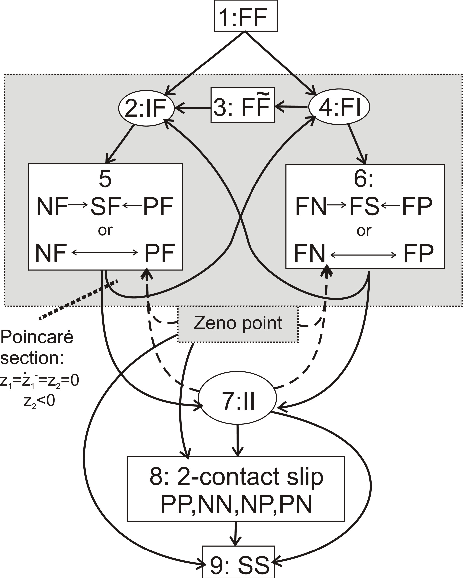
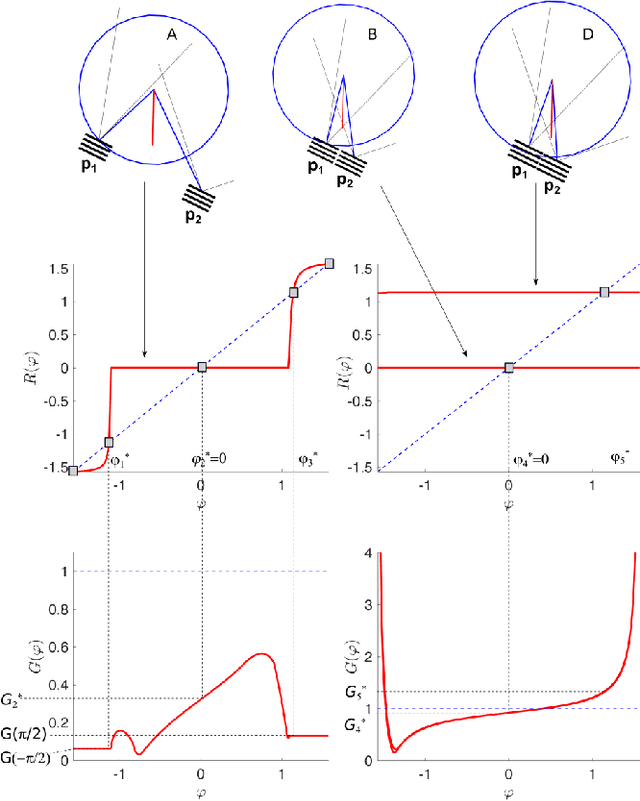
Abstract:Lyapunov stability of a mechanical system means that the dynamic response stays bounded in an arbitrarily small neighborhood of a static equilibrium configuration under small perturbations in positions and velocities. This type of stability is highly desired in robotic applications that involve multiple unilateral contacts. Nevertheless, Lyapunov stability analysis of such systems is extremely difficult, because even small perturbations may result in hybrid dynamics where the solution involves many nonsmooth transitions between different contact states. This paper concerns with Lyapunov stability analysis of a planar rigid body with two frictional unilateral contacts under inelastic impacts, for a general class of equilibrium configurations under a constant external load. The hybrid dynamics of the system under contact transitions and impacts is formulated, and a \Poincare map at two-contact states is introduced. Using invariance relations, this \Poincare map is reduced into two semi-analytic scalar functions that entirely encode the dynamic behavior of solutions under any small initial perturbation. These two functions enable determination of Lyapunov stability or instability for almost any equilibrium state. The results are demonstrated via simulation examples and by plotting stability and instability regions in two-dimensional parameter spaces that describe the contact geometry and external load.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge