Preference-Based Learning for User-Guided HZD Gait Generation on Bipedal Walking Robots

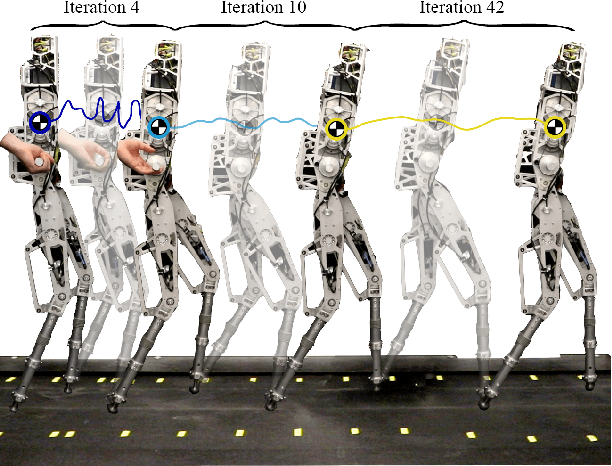
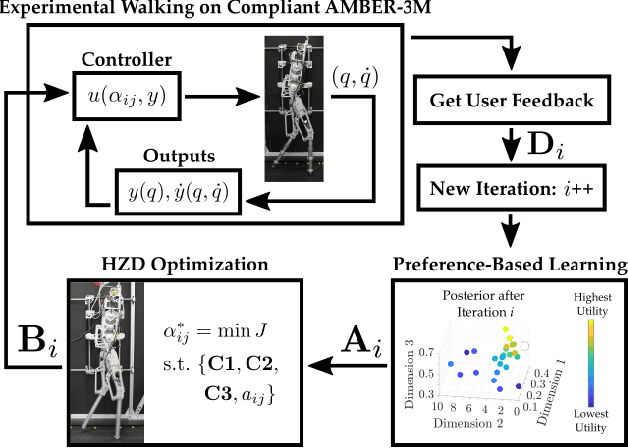
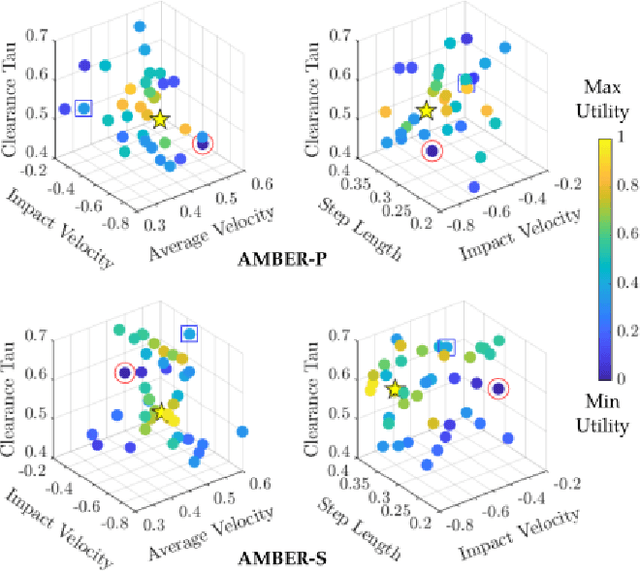
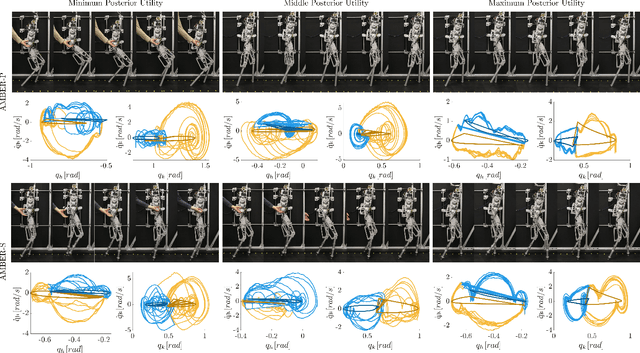
This paper presents a framework that unifies control theory and machine learning in the setting of bipedal locomotion. Traditionally, gaits are generated through trajectory optimization methods and then realized experimentally -- a process that often requires extensive tuning due to differences between the models and hardware. In this work, the process of gait realization via hybrid zero dynamics (HZD) based optimization problems is formally combined with preference-based learning to systematically realize dynamically stable walking. Importantly, this learning approach does not require a carefully constructed reward function, but instead utilizes human pairwise preferences. The power of the proposed approach is demonstrated through two experiments on a planar biped AMBER-3M: the first with rigid point feet, and the second with induced model uncertainty through the addition of springs where the added compliance was not accounted for in the gait generation or in the controller. In both experiments, the framework achieves stable, robust, efficient, and natural walking in fewer than 50 iterations with no reliance on a simulation environment. These results demonstrate a promising step in the unification of control theory and learning.

From Bipedal Walking to Quadrupedal Locomotion: Full-Body Dynamics Decomposition for Rapid Gait Generation

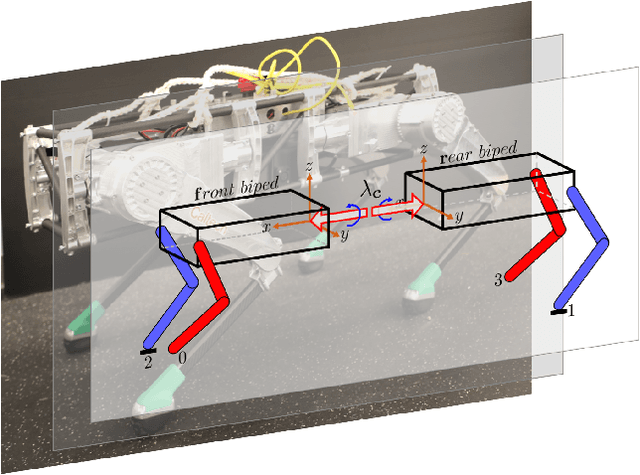
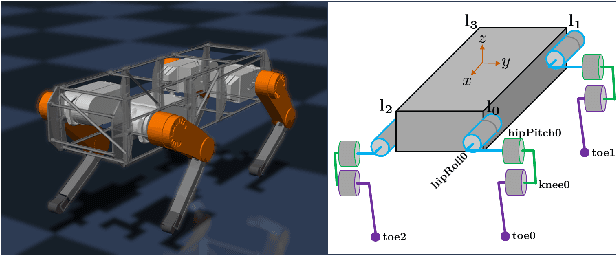
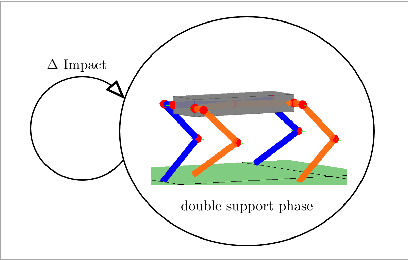
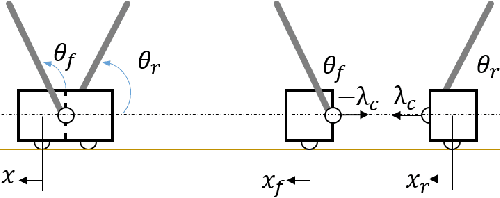
This paper systematically decomposes quadrupeds into bipeds to rapidly generate walking gaits, and then recomposes these gaits to obtain quadrupedal locomotion. We begin by decomposing the full-order, nonlinear and hybrid dynamics of a three-dimensional quadrupedal robot, including its continuous and discrete dynamics, into two bipedal systems that are subject to external forces. Using the hybrid zero dynamics (HZD) framework, gaits for these bipedal robots can be rapidly generated (on the order of seconds) along with corresponding controllers. The decomposition is performed in such a way that the bipedal walking gaits and controllers can be composed to yield dynamic walking gaits for the original quadrupedal robot --- the result, therefore, is the rapid generation of dynamic quadruped gaits utilizing the full-order dynamics. This methodology is demonstrated through the rapid generation (3.96 seconds on average) of four stepping-in-place gaits and one ambling gait at 0.35 m/s on a quadrupedal robot --- the Vision 60, with 36 state variables and 12 control inputs --- both in simulation and through outdoor experiments. This suggested a new approach for fast quadrupedal trajectory planning using full-body dynamics, without the need for empirical model simplification, wherein methods from dynamic bipedal walking can be directly applied to quadrupeds.

First Steps Towards Full Model Based Motion Planning and Control of Quadrupeds: A Hybrid Zero Dynamics Approach

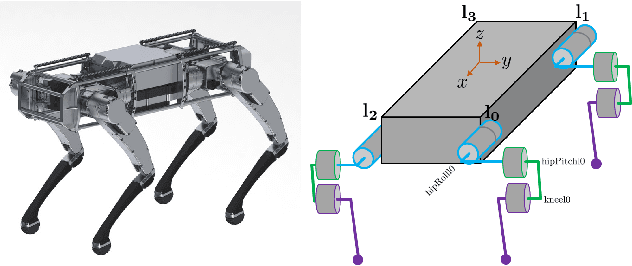
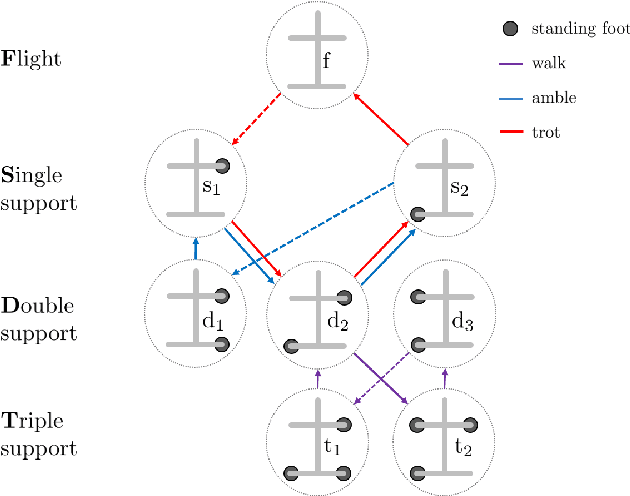
The hybrid zero dynamics (HZD) approach has become a powerful tool for the gait planning and control of bipedal robots. This paper aims to extend the HZD methods to address walking, ambling and trotting behaviors on a quadrupedal robot. We present a framework that systematically generates a wide range of optimal trajectories and then provably stabilizes them for the full-order, nonlinear and hybrid dynamical models of quadrupedal locomotion. The gait planning is addressed through a scalable nonlinear programming using direct collocation and HZD. The controller synthesis for the exponential stability is then achieved through the Poincar\'e sections analysis. In particular, we employ an iterative optimization algorithm involving linear and bilinear matrix inequalities (LMIs and BMIs) to design HZD-based controllers that guarantee the exponential stability of the fixed points for the Poincar\'e return map. The power of the framework is demonstrated through gait generation and HZD-based controller synthesis for an advanced quadruped robot, ---Vision 60, with 36 state variables and 12 control inputs. The numerical simulations as well as real world experiments confirm the validity of the proposed framework.

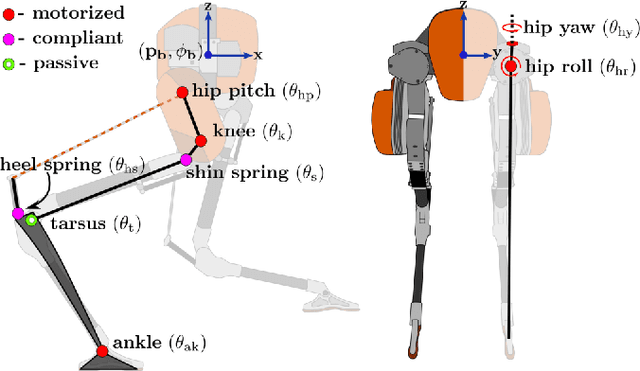
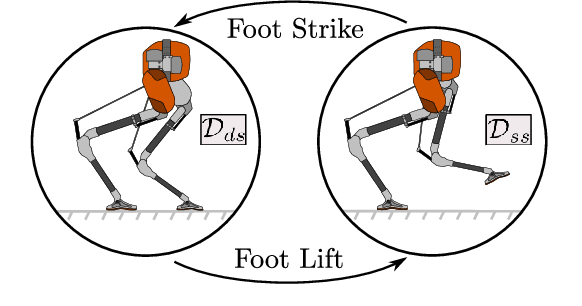
Dynamic Walking with Compliance on a Cassie Bipedal Robot

The control of bipedal robotic walking remains a challenging problem in the domains of computation and experiment, due to the multi-body dynamics and various sources of uncertainty. In recent years, there has been a rising trend towards model reduction and the design of intuitive controllers to overcome the gap between assumed model and reality. Despite its viability in practical implementation, this local representation of true dynamics naturally indicate limited scalibility towards more dynamical behaviors. With the goal of moving towards increasingly dynamic behaviors, we leverage the detailed full body dynamics to generate controllers for the robotic system which utilizes compliant elements in the passive dynamics. In this process, we present a feasible computation method that yields walking trajectories for a highly complex robotic system. Direct implementation of these results on physical hardware is also performed with minimal tuning and heuristics. We validate the suggested method by applying a consistent control scheme across simulation, optimization and experiment, the result is that the bipedal robot Cassie walks over a variety of indoor and outdoor terrains reliably.

Dynamic Walking on Slippery Surfaces: Demonstrating Stable Bipedal Gaits with Planned Ground Slippage

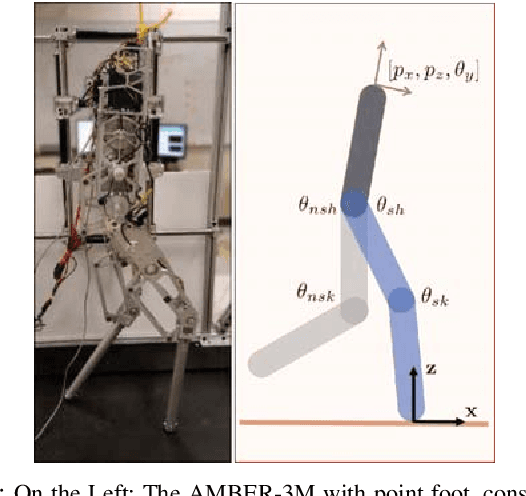
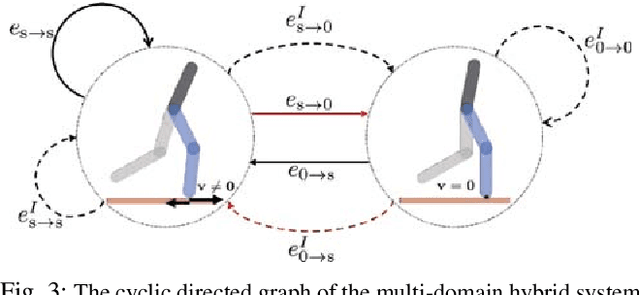
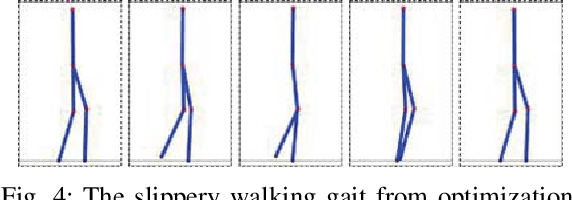
Dynamic bipedal robot locomotion has achieved remarkable success due in part to recent advances in trajectory generation and nonlinear control for stabilization. A key assumption utilized in both theory and experiments is that the robot's stance foot always makes no-slip contact with the ground, including at impacts. This assumption breaks down on slippery low-friction surfaces, as commonly encountered in outdoor terrains, leading to failure and loss of stability. In this work, we extend the theoretical analysis and trajectory optimization to account for stick-slip transitions at point foot contact using Coulomb's friction law. Using AMBER-3M planar biped robot as an experimental platform, we demonstrate for the first time a slippery walking gait which can be stabilized successfully both on a lubricated surface and on a rough no-slip surface. We also study the influence of foot slippage on reducing the mechanical cost of transport, and compare energy efficiency in both numerical simulations and experimental measurements.